目次
はじめに
どーも、将棋と筋トレが好きな学生エンジニアのゆうき(@engieerblog_Yu)です。
今回はPyTorchを使って、簡単なニューラルネットワークのモデル学習をしていきたいと思います。
ライブラリのインポート
今回は、PyTorchとmatplotlibを使用します。
import torch
import torch.nn as nn
import torch.optim as optim
import matplotlib.pyplot as plt今回やりたいこと
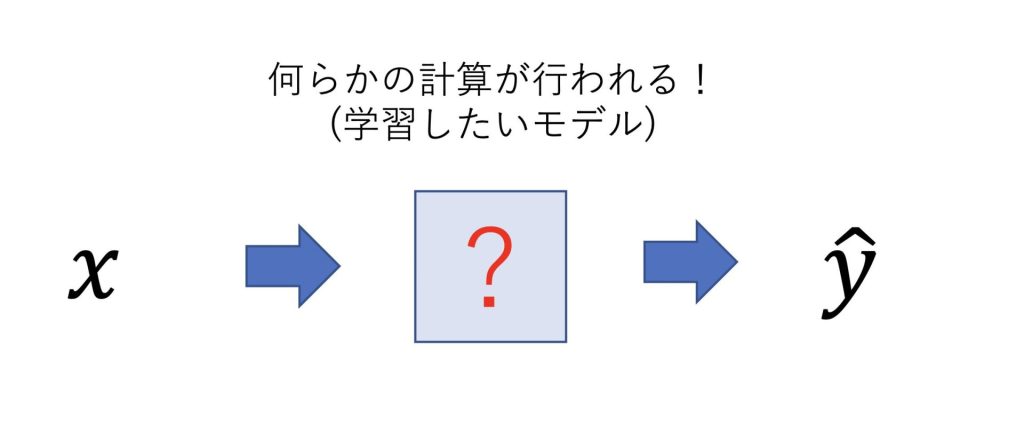
今回は、入力xに対して、あるyを出力することができるようなニューラルネットワークを作成していきます。
具体的に説明するとxに対して、何らかの計算を行った値がyになります。
ニューラルネットワークのモデルは、xが計算されてyになる時に、どのような計算を行っているのかはわかりません。
ニューラルネットワークは予測した値と正解の値の誤差が小さくなるように、自分自身を改善していきます。
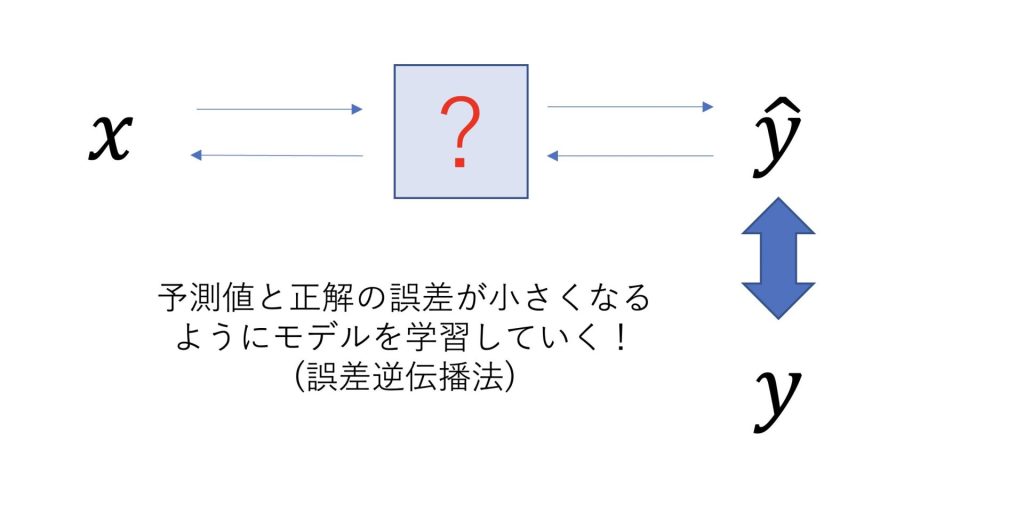
この時、誤差を定義したものが損失関数と言われ、モデルを最適化するものが最適化関数と言われます。
誤差逆伝播法については、以下の記事でも触れています。
ニューラルネットワークを定義する
今回は簡単のために、y = wx + bとします。
これは線形的な関数ですので、ニューラルネットワークに線形レイヤ(Linear Layer)を設定してあげましょう。
class Net(nn.Module):
def __init__(self):
super(Net,self).__init__()
self.lin1 = nn.Linear(in_features=20,out_features=20,bias=False)
def forward(self,x):
x = self.lin1(x)
return x今回は軽量のプログラムですが、GPUを使っています。
Google CoraboratoryのGPUの使い方に関しましてはこちらの記事をどうぞ。
損失関数に最小二乗誤差を使って比較した場合
最小二乗誤差の定義については以下の記事で解説しています。
def main_mse(optimizer):
net = Net()
net.to('cuda')
loss_list = []
#入力x(要素が20のベクトル)
x = torch.randn(1,20).to('cuda')
#重みw(これを学習していく)
w = torch.randn(1,1).to('cuda')
#出力y
y = torch.mul(w,x) + 2
#最小二乗誤差
criterion = nn.MSELoss()
#確率的勾配降下法(sgd)
if optimizer == "sgd":
optimizer = optim.SGD(net.parameters(),lr=0.1)
#モーメンタム法
if optimizer == "momentum_sgd":
optimizer = optim.SGD(net.parameters(),lr=0.1,momentum=0.9)
#Adam法
if optimizer == "adam":
optimizer = optim.Adam(net.parameters(),lr=0.1,betas=(0.9,0.99),eps=1e-09)
#RMSprop法
if optimizer == "rmsprop":
optimizer = optim.RMSprop(net.parameters())
#モデルの学習
for epock in range(40):
optimizer.zero_grad()
y_pred = net(x)
loss = criterion(y_pred,y)
loss.backward()
optimizer.step()
loss_list.append(loss.data.item())
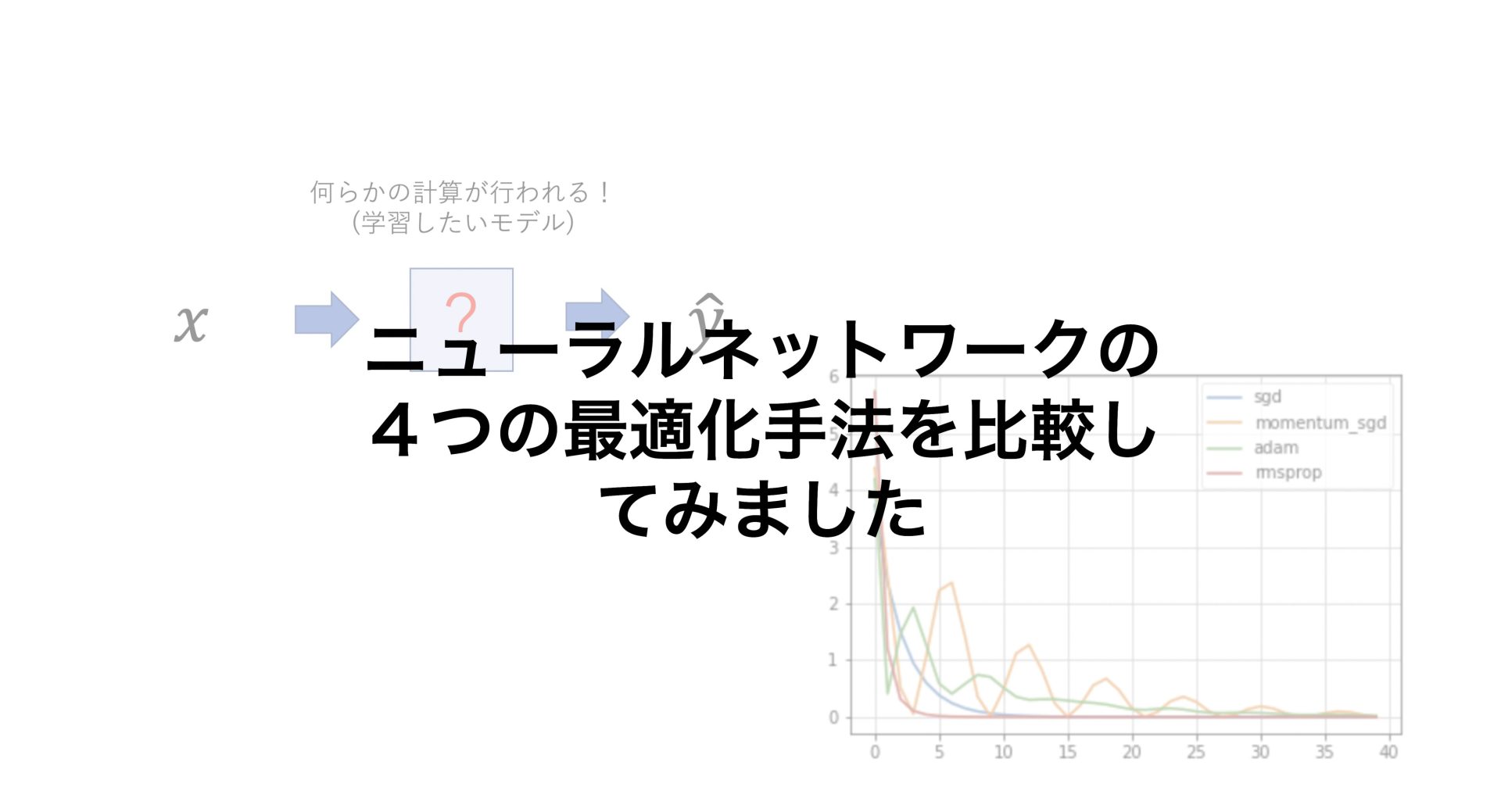
return loss_listそれでは、最適化手法ごとにタイムステップに応じて、どのように最適化されていくのかプロットしてみます。
loss_dict = {}
loss_dict["sgd"] = {}
loss_dict["momentum_sgd"] = {}
loss_dict["adam"] = {}
loss_dict["rmsprop"] = {}
for key,value in loss_dict.items():
loss_dict[key] = main_mse(key)
plt.figure()
plt.plot(loss_dict["sgd"],label='sgd')
plt.plot(loss_dict["momentum_sgd"],label='momentum_sgd')
plt.plot(loss_dict["adam"],label='adam')
plt.plot(loss_dict["rmsprop"],label='rmsprop')
plt.legend()
plt.grid()縦軸が誤差の値で、横軸がタイムステップのグラフを表示することができました。
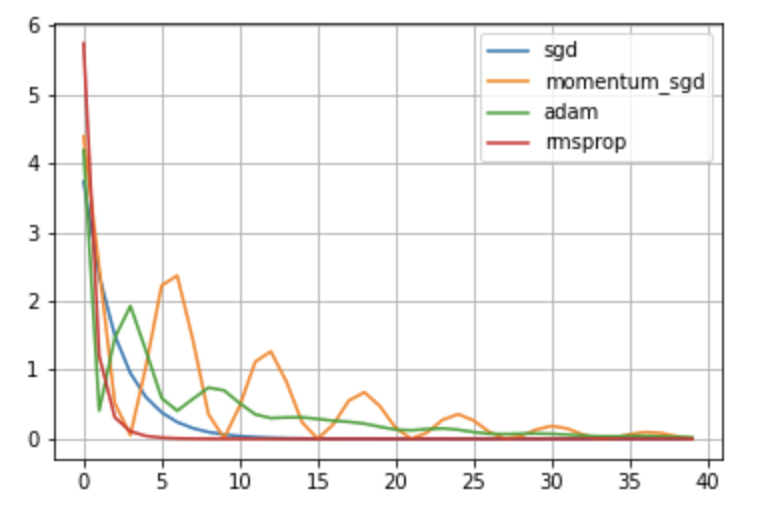
今回の例では、rmspropが最も早く誤差を0にできていることがわかります。
Momentum法は、SGD(確率的勾配降下法)に、物理法則を取り入れたもので、ボールがお椀の上を転がるような動きをします。
SGDに減衰性を取り入れた手法に、AdaGrad法というものがあります。
Adamは、Momentum法とAdaGrad法を組み合わせたような手法です。
よってAdamは振動が起こっていますが、Momentum法よりも早く減衰していることがわかります。
それぞれの最適関数の具体的なアルゴリズムについては、以下の記事で解説しています。
損失関数に平均絶対誤差を使って比較した場合
次に損失関数に平均絶対誤差を使ってみます。
平均絶対誤差とは、単に予測値と正解の差の絶対値をとったものです。
それでは先ほどと同様に実装していきます。
def main_l1_loss(optimizer):
net = Net()
net.to('cuda')
loss_list = []
x = torch.randn(1,20).to('cuda')
w = torch.randn(1,1).to('cuda')
y = torch.mul(w,x) + 2
#平均絶対誤差
criterion = nn.L1Loss()
if optimizer == "sgd":
optimizer = optim.SGD(net.parameters(),lr=0.1)
if optimizer == "momentum_sgd":
optimizer = optim.SGD(net.parameters(),lr=0.1,momentum=0.9)
if optimizer == "adam":
optimizer = optim.Adam(net.parameters(),lr=0.1,betas=(0.9,0.99),eps=1e-09)
if optimizer == "rmsprop":
optimizer = optim.RMSprop(net.parameters())
#モデルの学習
for epock in range(40):
optimizer.zero_grad()
y_pred = net(x)
loss = criterion(y_pred,y)
loss.backward()
optimizer.step()
loss_list.append(loss.data.item())
return loss_listloss_dict = {}
loss_dict["sgd"] = {}
loss_dict["momentum_sgd"] = {}
loss_dict["adam"] = {}
loss_dict["rmsprop"] = {}
for key,value in loss_dict.items():
loss_dict[key] = main_l1_loss(key)
plt.figure()
plt.plot(loss_dict["sgd"],label='sgd')
plt.plot(loss_dict["momentum_sgd"],label='momentum_sgd')
plt.plot(loss_dict["adam"],label='adam')
plt.plot(loss_dict["rmsprop"],label='rmsprop')
plt.legend()
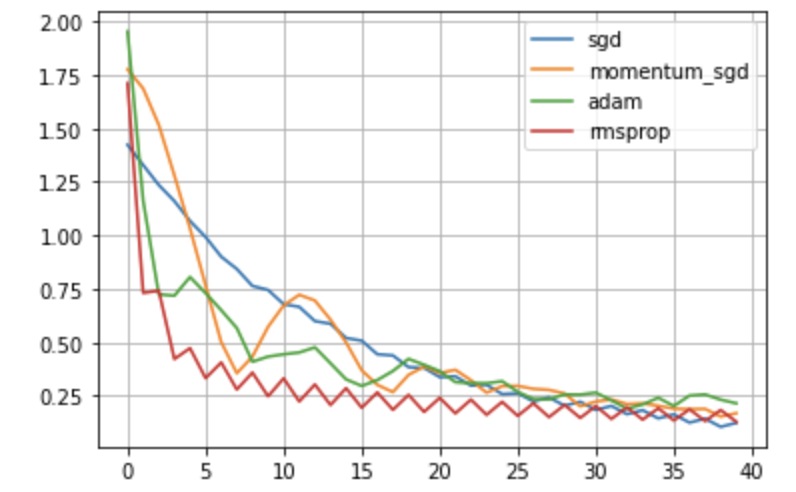
plt.grid()最小二乗誤差とは異なり、誤差をほとんど0にすることはできませんでしたが、それぞれの最適化手法によって、動き方が異なることがわかります。
終わりに

今回はPyTorchを用いて、単純なニューラルネットワークを学習しました。
最適化手法によって、最適値への近づき方が異なることがわかっていただけたかと思います。
最適化手法は、どれが優れているというものではなく、場面に応じて適切なものを選択することが大切になってきます。
ただ研究者の中で人気なものはAdamなようで、自分も困ったらまずはAdamを使うようにしています。
最適化手法のアルゴリズムを理解したい方は、SGD(確率的勾配降下法)から理解していくのがおすすめです。

最後まで読んでいただきありがとうございました。

他にもいろんな記事があるにゃ。
AI美女生成に興味がある方
Stable Diffusionを使ってAI美女を生成する方法についてもnoteで解説しています。








コメント