はじめに
こんにちは。将棋と筋トレが好きな、情報系大学生のゆうき(@engieerblog_Yu)です。
今回は前回のパーセプトロンから、ニューラルネットワークを考えるために、活性化関数について触れていきたいと思います。
パーセプトロンとニューラルネットワークの違い
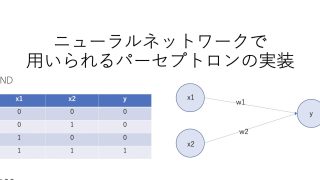
パーセプトロンは前回の記事で、以下のように表されると学びました。
(今回θの値は0とします。)
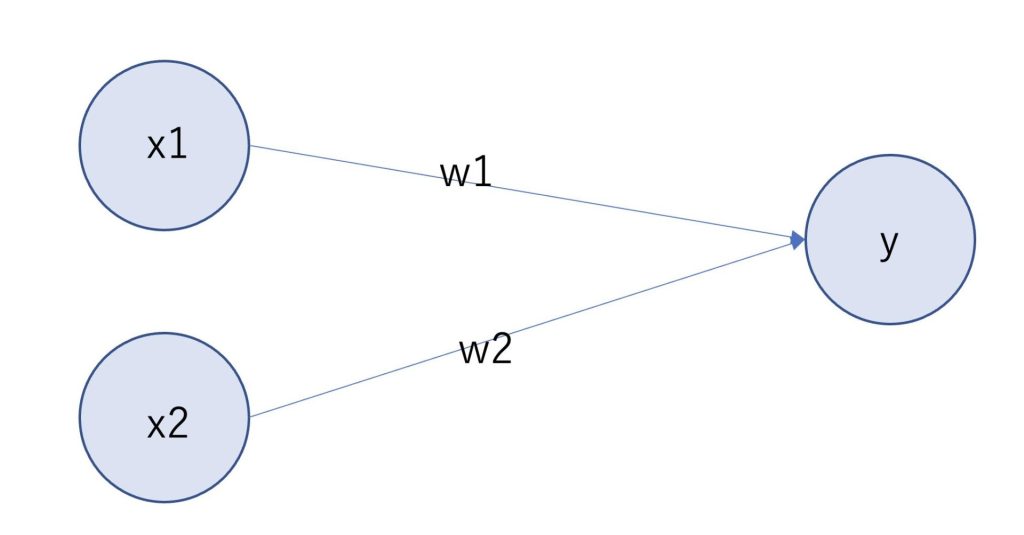
\(w_1×x_1+w_2×x_2+b=k\)
\(k<=0 → y=0\)
\(k>0→ y=1\)
ここで活性化関数を以下のように定義します。
\( h(x)= \begin{cases} 1 & \text{if $x>0$} \\ 0 & \text{if $x<=0$} \end{cases}\)
するとyは
\(y = h(w_1×x_1+w_2×x_2+b)\)
と表すことができます。
図で活性化関数を明示的に表したものが以下です。
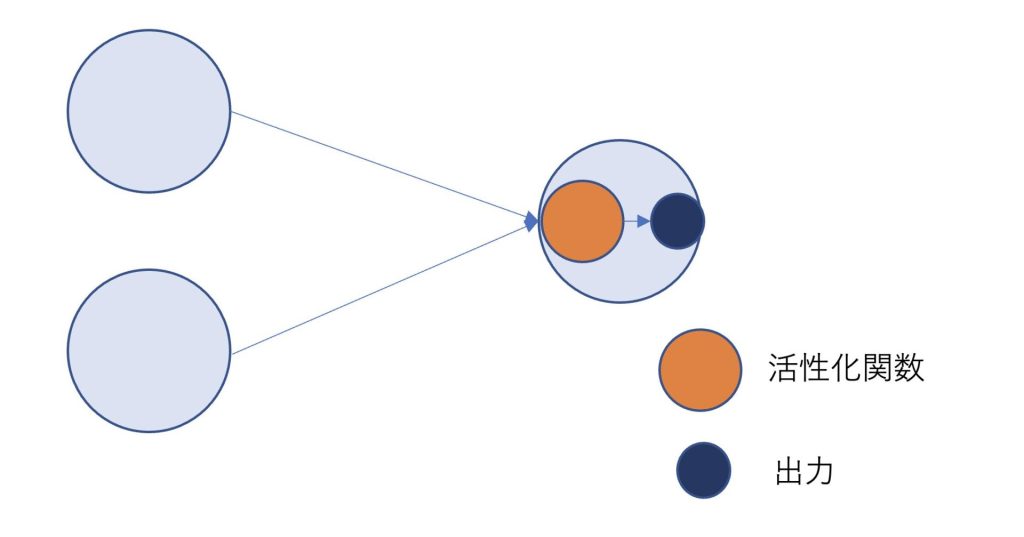
しかしパーセプトロンには、コンピュータの複雑な処理を行うことができるという良い面がある一方で、重みを人力で決めなければいけないといった悪い面がありました。
そこで重みを自動で学習できないかといった理由から考えられたものが、ニューラルネットワークです。
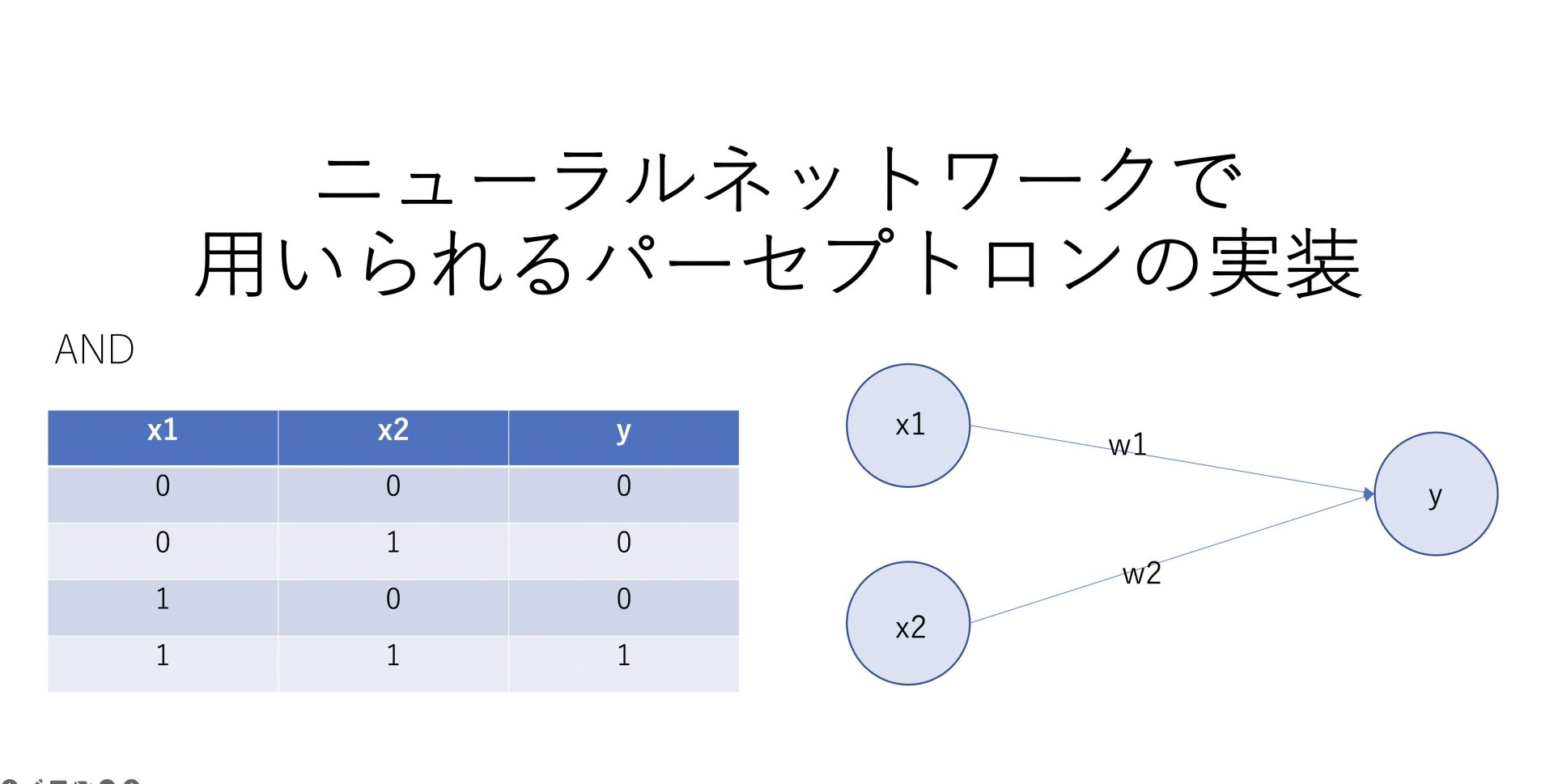
ニューラルネットワークは入力層と中間層と出力層から構成されています。
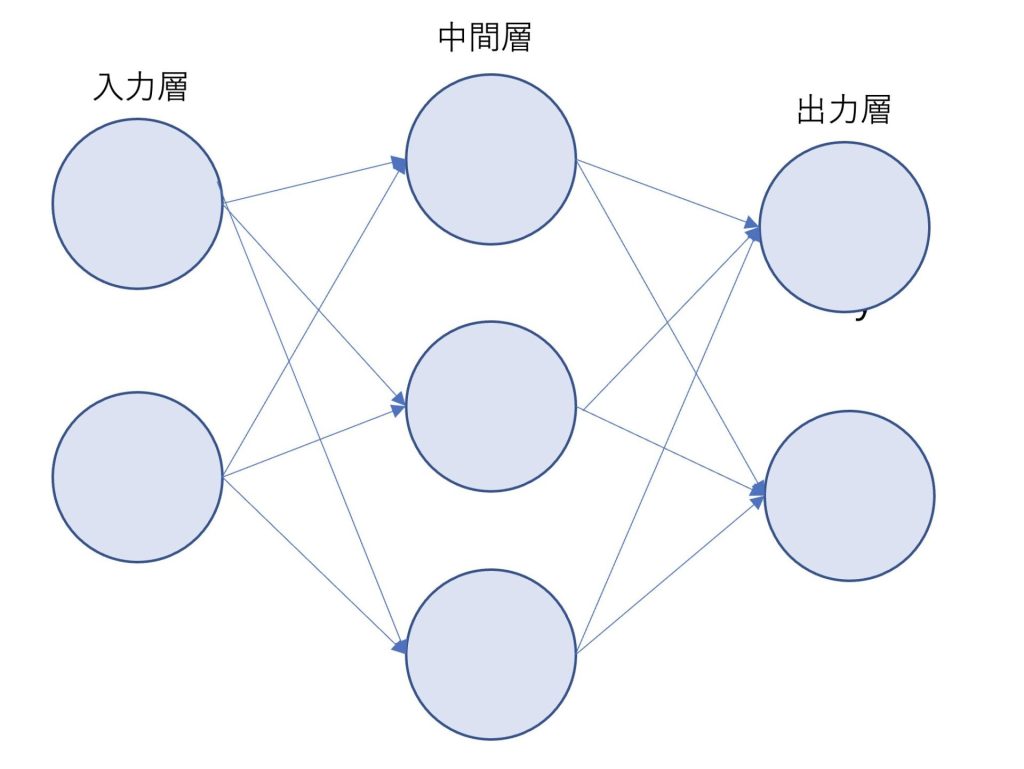
先ほど述べた活性化関数はパーセプトロンと類似して、このように図示することができます。
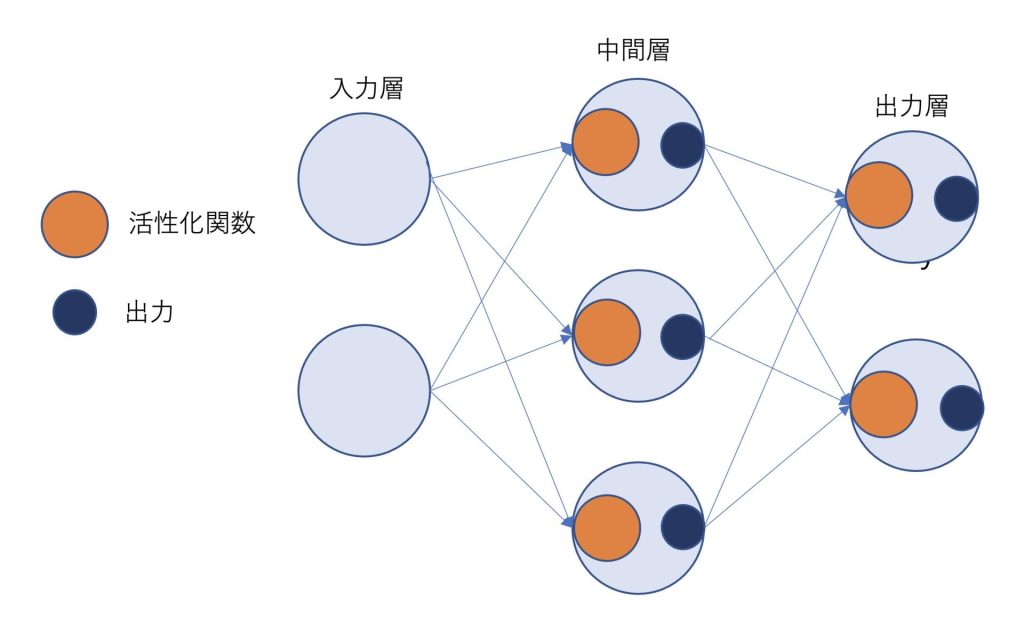
今回はニューラルネットワークで使われる活性化関数について、Pythonで実装しながらまとめていきたいと思います。
パーセプトロンはコンピュータの処理を表現することができる一方で重みを手動で決めなければいけないというデメリットがあった
重みを自動で学習できるようにしたものがニューラルネットワーク
ステップ関数
ステップ関数は、パーセプトロンで使われている活性化関数です。
パーセプトロンではある値θを超えるとニューロンが発火して、yが1になりますが、その部分に対応します。
\( h(x)= \begin{cases} 1 & \text{if $x>0$} \\ 0 & \text{if $x<=0$} \end{cases}\)
def step(x):
return np.array(x>0)
x = np.arange(-5.0,5.0,0.1)
y = step(x)
plt.plot(x,y)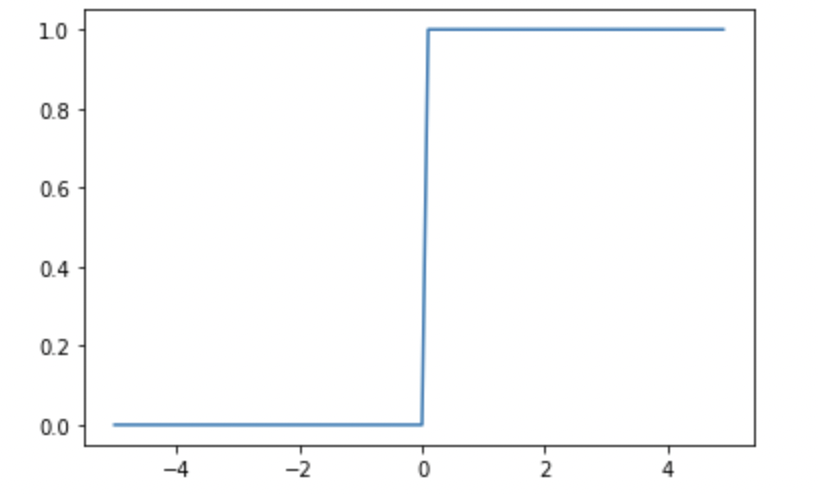
ステップ関数は、パーセプトロンの活性化関数として使われている
微分値は、0以外の場所で0となる
シグモイド関数
先ほどのステップ関数をなめらかに表したものを、シグモイド関数と言います。
\(h(x)=\frac{1}{1+e^{-x}}\)
def sigmoid(x):
return 1/(1+np.exp(-x))
x = np.arange(-5.0,5.0,0.1)
y = sigmoid(x)
plt.plot(x,y)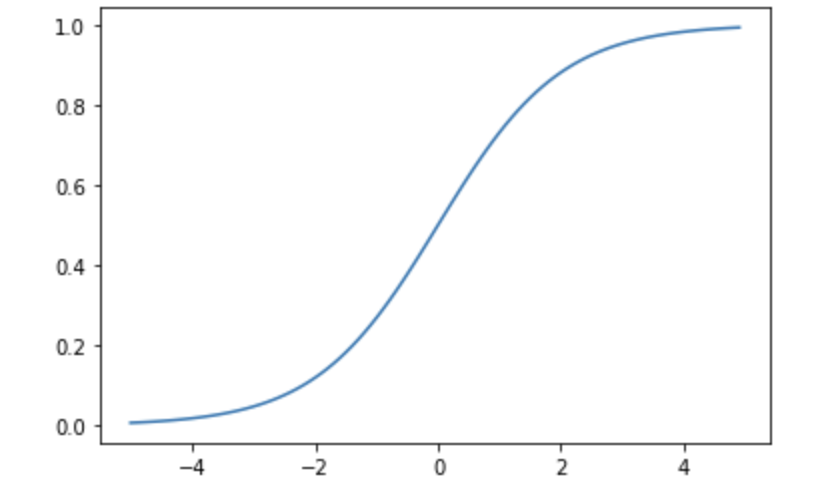
ステップ関数に対して、シグモイド関数は滑らかで、微分値が0とならない
ReLu関数
上記の二つの関数に対して、最近用いられるようになってきている活性化関数としてReLU関数といったものもあります。
\( h(x)= \begin{cases} x & \text{if $x>0$} \\ 0 & \text{if $x<=0$} \end{cases}\)
def relu(x):
return np.maximum(0,x)
x = np.arange(-5.0,5.0,0.1)
y = relu(x)
plt.plot(x,y)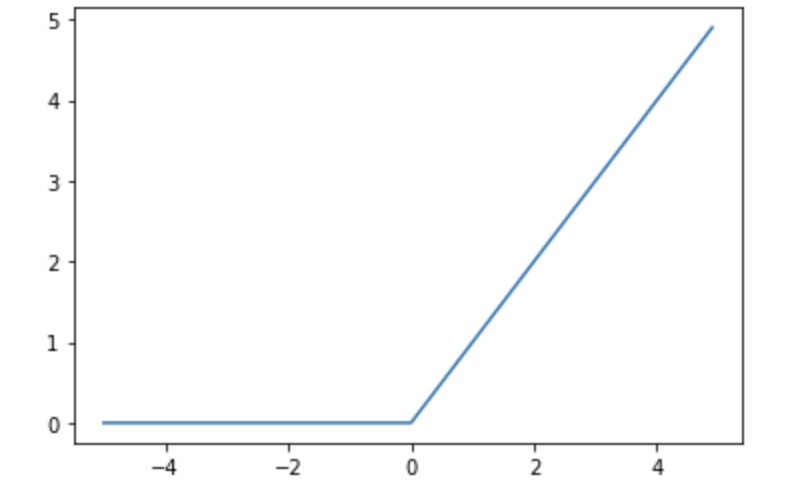
最近ではReLU関数が用いられるようになってきている
活性化関数に線形関数が使われない理由

活性化関数にy=axなどの線形関数は使われません。
なぜなら何層にも重ねられているニューラルネットワークにおいて線形関数を活性化関数として用いても、何の意味もないからです。
a×a×aとしても、y=cx(c=a^3)と表現することができてしまいます。
まとめ
パーセプトロンはコンピュータの処理を表現することができる一方で重みを手動で決めなければいけないというデメリットがあった
重みを自動で学習できるようにしたものがニューラルネットワーク
ステップ関数は、パーセプトロンの活性化関数として使われており、微分値は、0以外の場所で0となる
ステップ関数に対して、シグモイド関数は滑らかで、微分値が0とならない
最近ではReLU関数が用いられるようになってきている
機械学習、ディープラーニングを学びたい方におすすめの入門書籍です。
ディープラーニングの理論が分かりやすくまとめられていて、力が身につくと思います。

最後まで読んでいただきありがとうございました。

他にもいろんな記事があるにゃ。


コメント