はじめに
どーも、将棋と筋トレが好きな学生エンジニアのゆうき(@engieerblog_Yu)です。
今回はデータサイエンスに必要な統計、ポアソン分布編ということで前回の続きとなる内容です!
二項分布について怪しい方は合わせてどうぞ。
ポアソン分布について
ポアソン分布の目的は、ある期間に事象がどれくらい発生するか?ということです。
例えば
1日にメールが何通届くか?
蛍は10秒間に何回光るか?
台風は1年に何回発生するか?
などのようなことです。
ポアソン分布は、平均値μとすると、以下のような式で表すことができます。
\(P_p(x)=\frac{μ^x}{x!}e^{-μ}\)
\(x=(0,1・・∞)\)
ポアソン分布は、前回まとめた二項分布と同じく離散的確率分布です。
グラフで表すと以下のようになります。
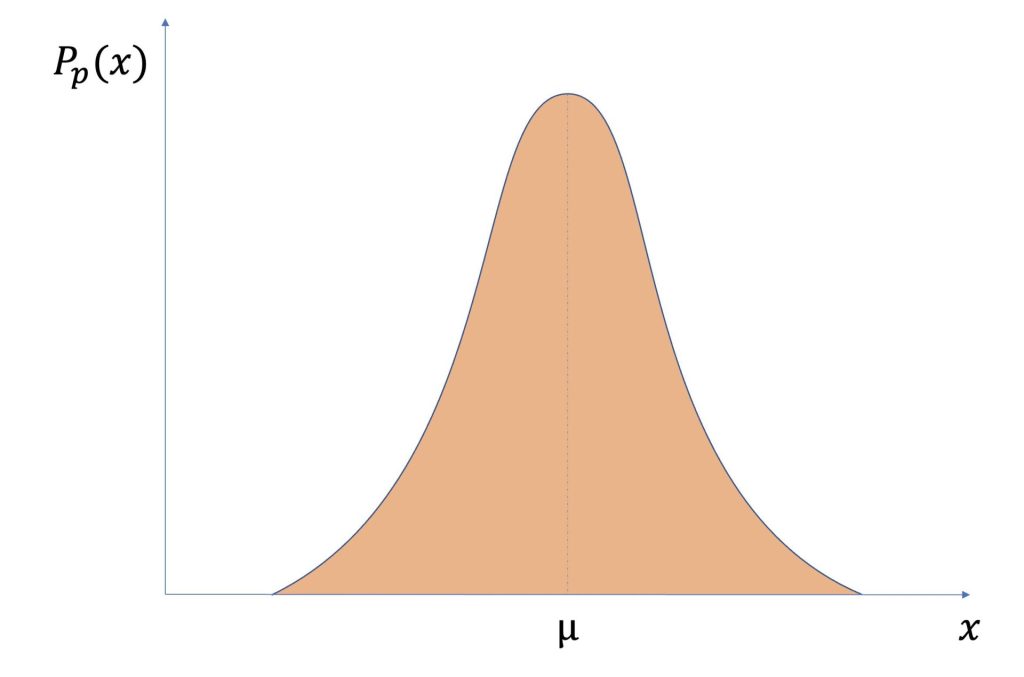
xは事象が発生する回数ですので、必ず正の整数です。
確率が高い部分ほど、たくさん出て確率が低い部分ほどあんまり出ないということになります。
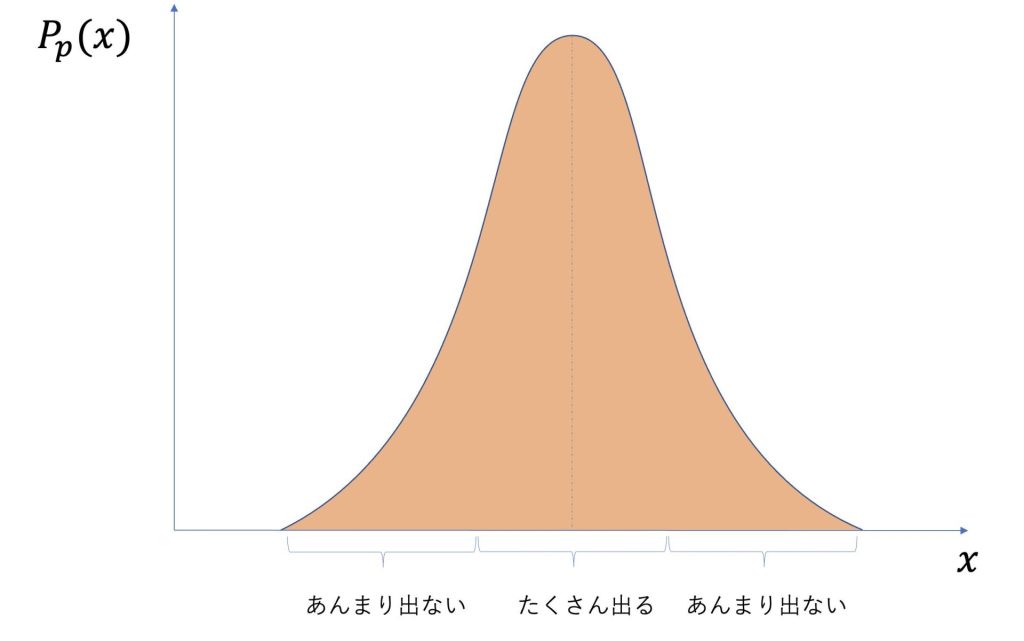
例えば一日にメールが来る平均が4件で、ポアソン分布に従うとすると、1日に来るメールの件数は大体4件で、100件や0件である確率は比較的小さいということになります。
それではポアソン分布を、二項分布から導出していこうと思います。
二項分布からポアソン分布を導出する
二項分布でポアソン分布を導出してみます。
二項分布の確率分布は、以下の式で表されると前回まとめました。
\(P_b(x)={}_n C_x(p)^{x}(1-p)^{n-x}\)
二項分布の期待値はμ=npと表されましたが、μを一定に保ちながらn→∞、p→0にするとポアソン分布となります。
それでは上記の式と条件から式を変形していきます。
\({}_n C_x(p)^{x}(1-p)^{n-x}\)
\(=\frac{n!}{x!(n-x)!}(\frac{μ}{n})^x(1-\frac{μ}{n})^{n-x}\)
\(=\frac{n(n-1)(n-2)・・(n-x+1)}{x!}(\frac{μ^x}{n^x})(1-\frac{μ}{n})^{n}(1-\frac{μ}{n})^{-x}\)
\(=\frac{n^x(1-\frac{1}{n})(1-\frac{2}{n})・・(1-\frac{x}{n}+\frac{1}{n})}{x!}(\frac{μ^x}{n^x})(1-\frac{μ}{n})^{n}(1-\frac{μ}{n})^{-x}\)
\(=\frac{(1-\frac{1}{n})(1-\frac{2}{n})・・(1-\frac{x}{n}+\frac{1}{n})}{x!}(μ^x)(1-\frac{μ}{n})^{n}(1-\frac{μ}{n})^{-x}\)ー①
ここで
\(-\frac{μ}{n}=h\)とおくと
\((1-\frac{μ}{n})^{n}\)
\(=((1+h)^h)^{-μ})\)
となり、n→∞でh→0となるので
\(=e^{-μ}\)となります。
よって①をn→∞としたものは
\(=\frac{μ^x}{x!}e^{-μ}\)
となります。
これは先ほどのポアソン分布の確率分布の式と一致します。
またポアソン分布の期待値と分散は、ともにμとなります。
まとめ
ポアソン分布は、二項分布の期待値μを一定に保つという条件下でn→∞、p→0にすることで導出できる
ポアソン分布は離散型確率分布であり、以下の式で表される
\(P_p(x)=\frac{μ^x}{x!}e^{-μ}\)
\(x=(0,1・・∞)\)
今回はデータサイエンスに用いる統計二回目として、二項分布からポアソン分布を導出していきました。
次回は、分布の中で最も有名な正規分布について、まとめていきたいと思います。

最後まで読んでいただきありがとうございました。

他にもいろんな記事があるにゃ。





コメント