はじめに
どーも、情報系大学生のゆうき(@engieerblog_Yu)です。
今回はコンピュータのプロセス管理やハフマン符号化、整列アルゴリズムなどに用いられる二分ヒープについてまとめていきたいと思います。
プログラムなどの特定の操作を、効率的に実行するために二分ヒープが使われています。
効率的なプログラミングをする上で、必要になってくることも多いのではないでしょうか。
オーダー記法について怪しい方はこちらの記事も併せてどうぞ。
2分ヒープ
二分ヒープは以下の条件を満たします。
親ノードよりも子ノードの値の方が大きい
広義の完全二分木になっている(全ての葉が左詰めになっている)
(親ノードよりも子ノードが小さいものとして二分ヒープを構成している場合もあります。)
二分ヒープは主に、挿入と最小値の削除を効率的に実行することができます。
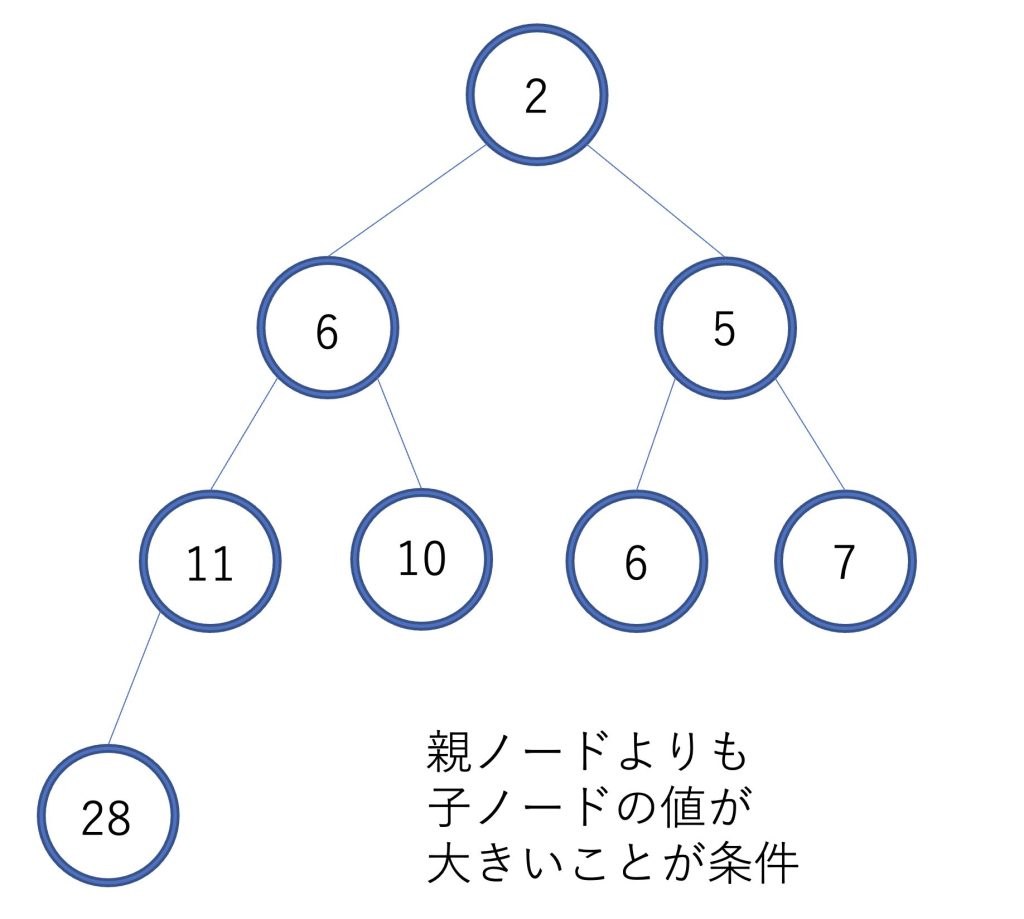
最小値の削除
二分ヒープの最小値の削除を行います。
この場合、最小値は必ず根の要素になります。
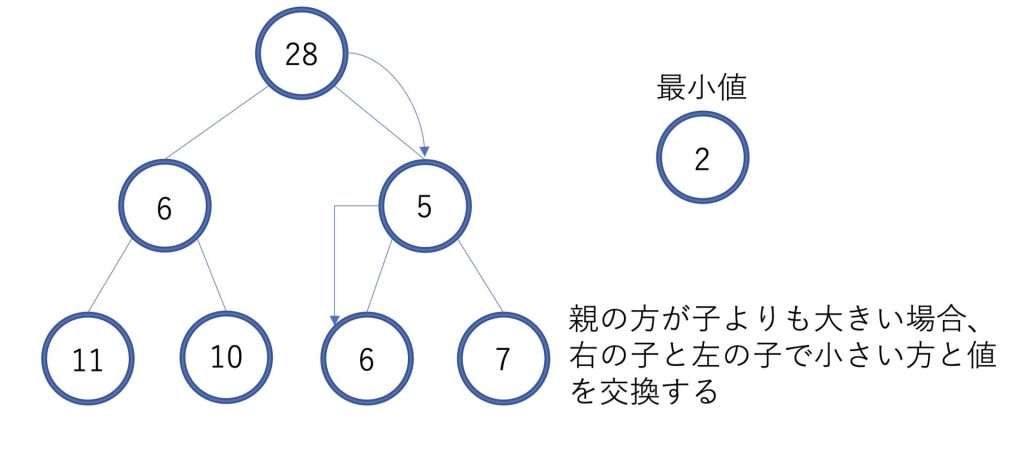
最小値を取り出したのちに二分ヒープの条件を満たすように、値を交換していきます。
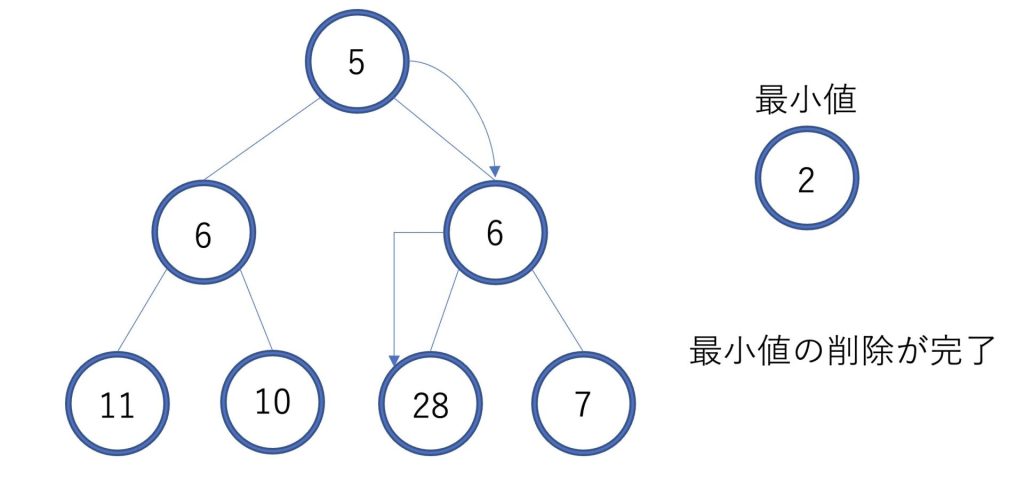
最小値を削除することができました。
最小値の削除の平均計算量はO(logn)となります。
挿入
次に新しい要素を挿入していきます。
まずヒープの最後に新しい要素を追加します。
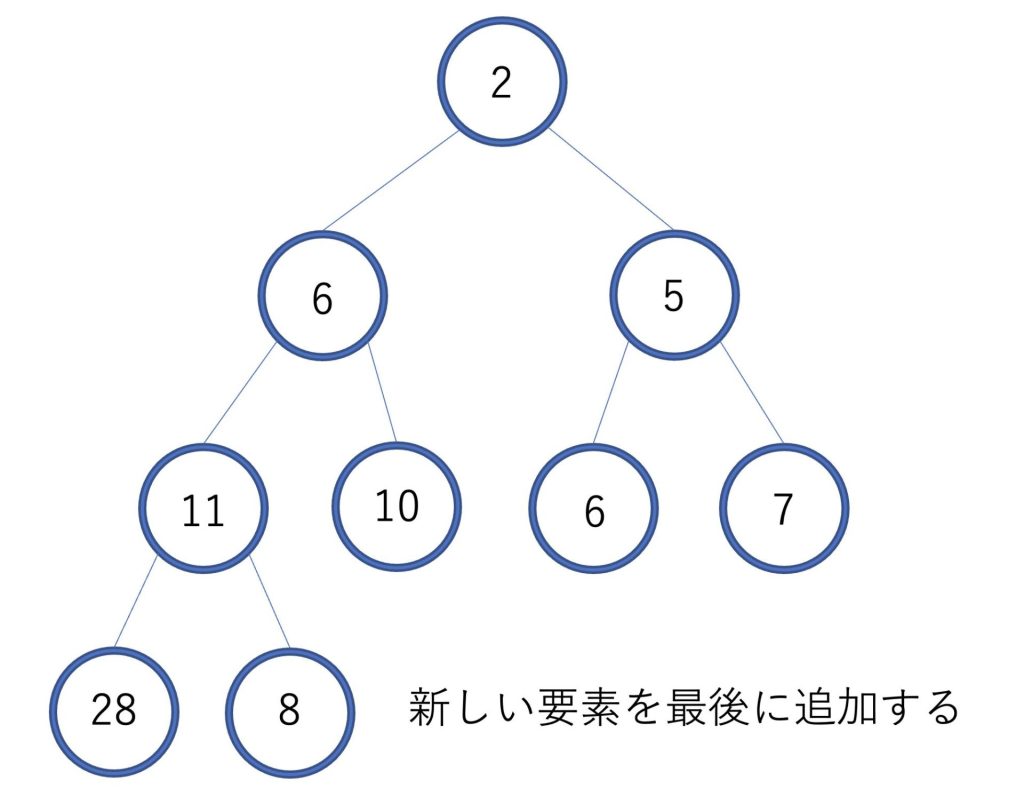
次に親<子を満たすように要素を交換していきます。
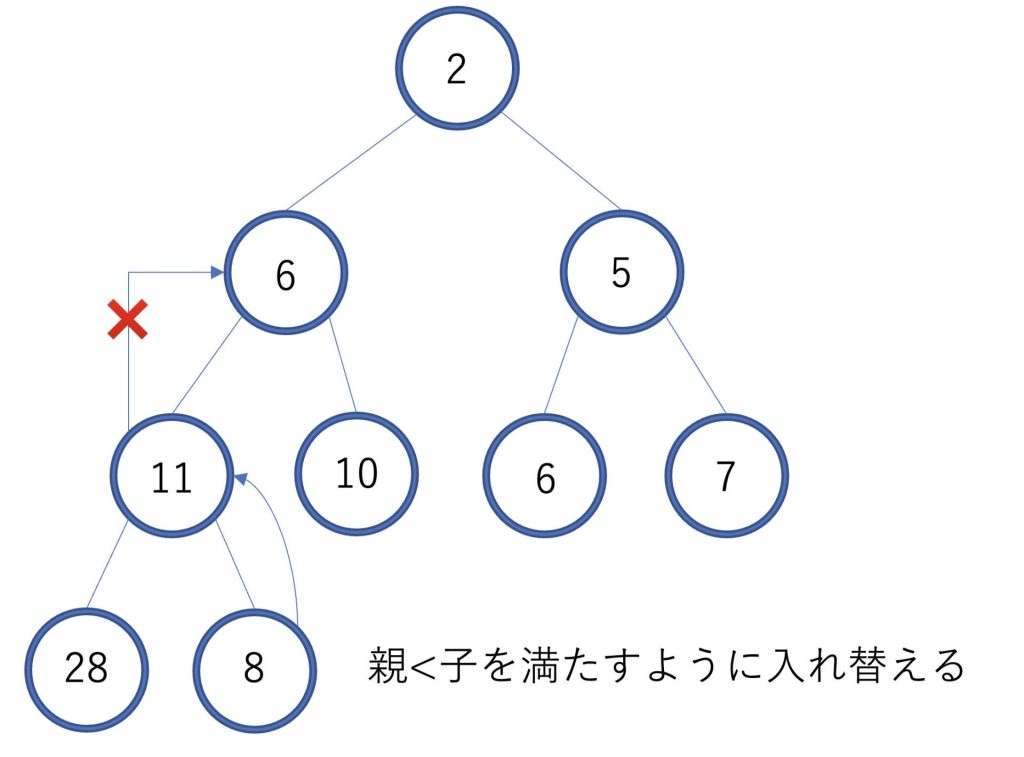
要素を挿入することができました。
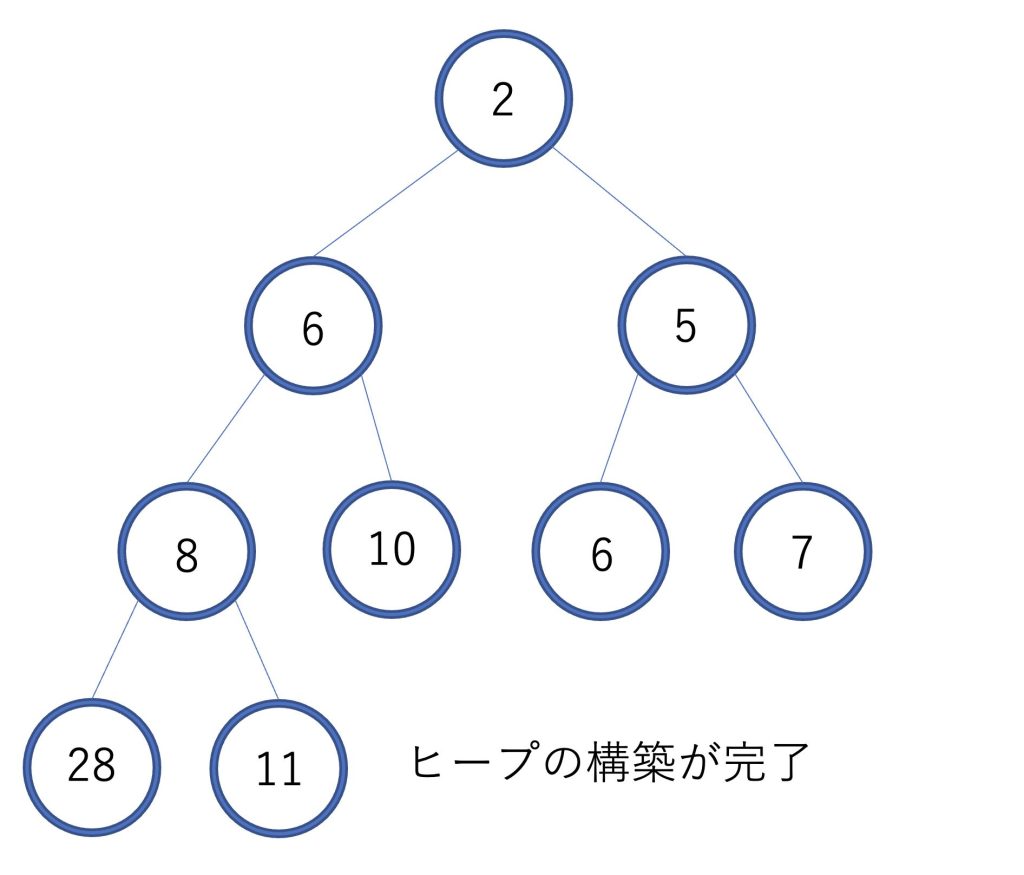
挿入も平均計算量はO(logn)となります。
2分探索木
二分探索木は以下の条件を満たします。
全ての接点において左にある子が自身の数より小さく、右にある子が自身の数より大きい
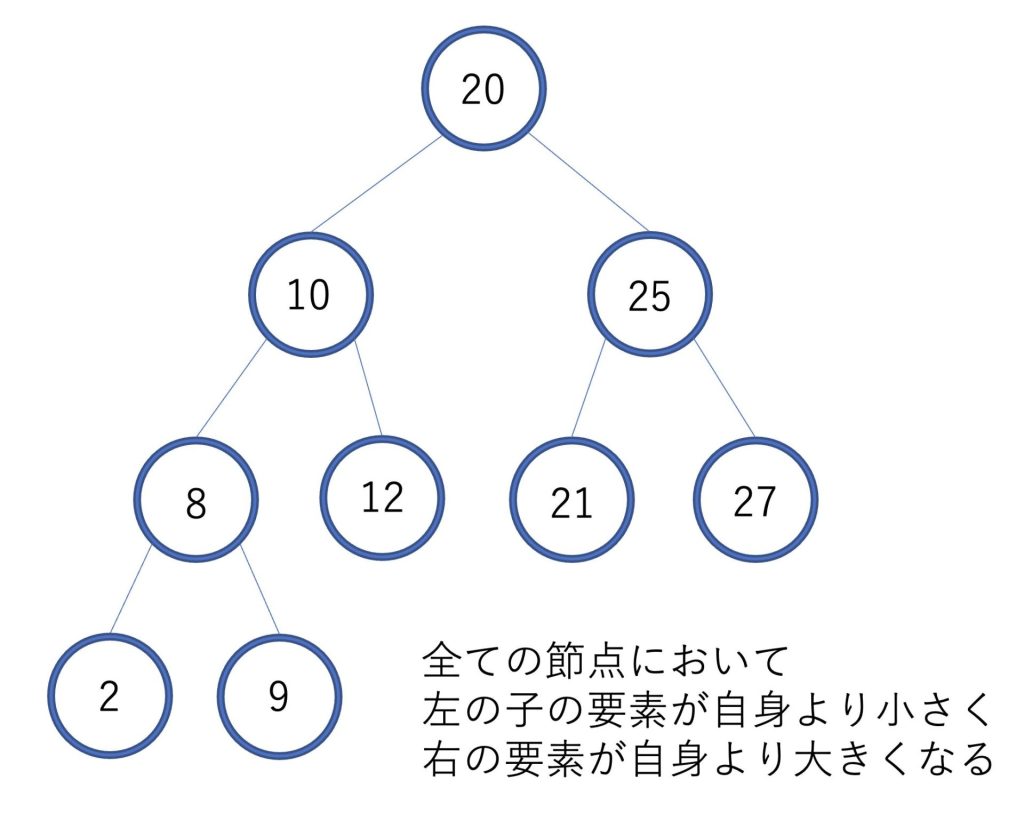
二分探索木は挿入、削除、探索、最小値の探索の計算が効率的にでき、それらの平均計算量は全てO(logn)です。
挿入
15という要素を挿入したいとします。
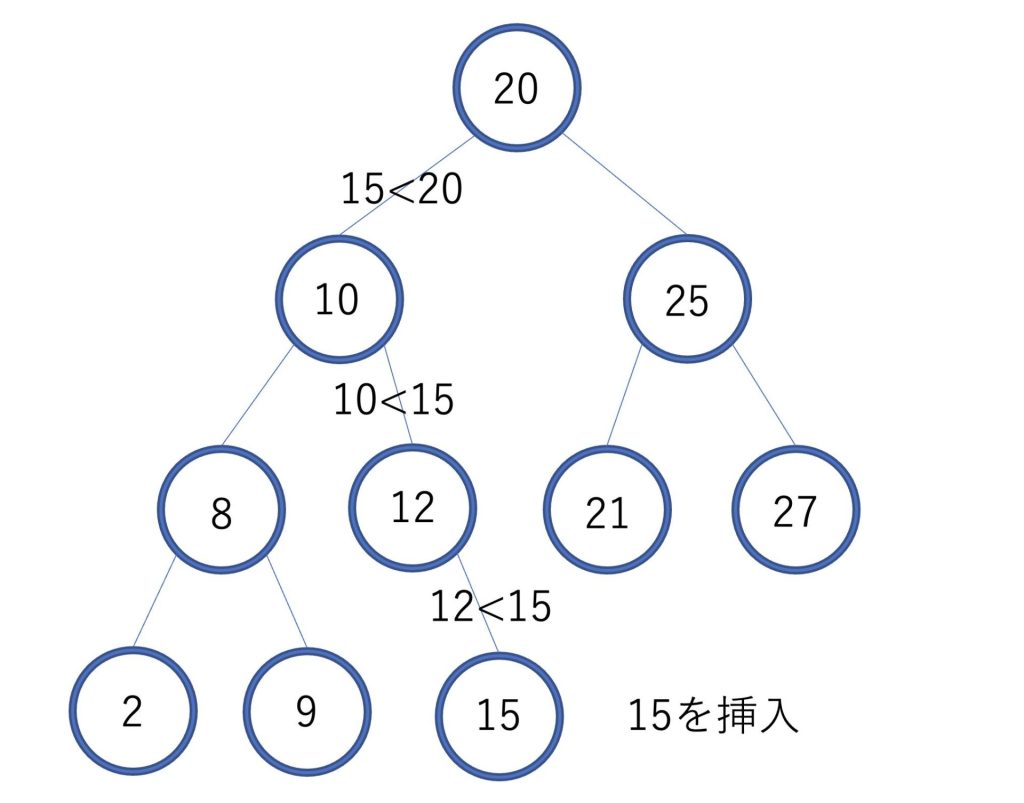
15は20よりも小さいので左の子に進みます。
15は10よりも大きいので右の子に進みます。
15は12よりも大きいので右の子に進みたいのですが、もう子がないので右の子に15を挿入します。
探索
21という要素を探索したいとします。
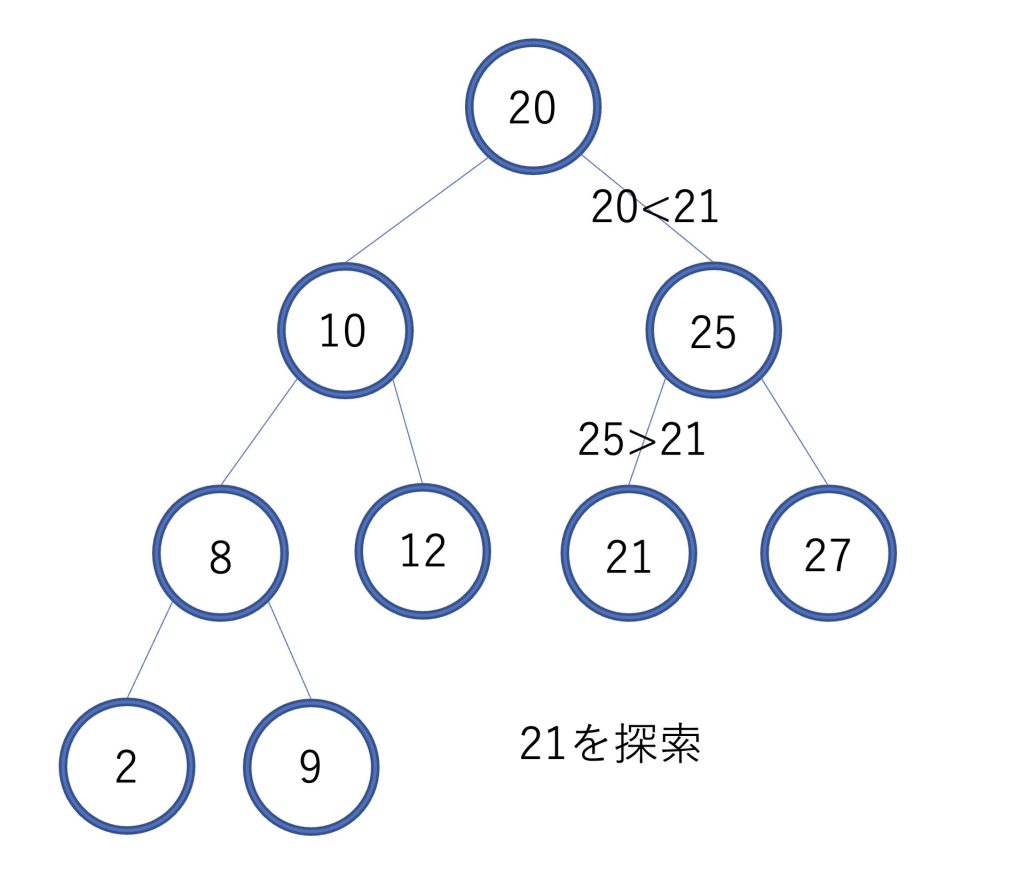
21は20よりも大きいので右の子に進みます。
21は25よりも小さいので左の子に進みます。
探索する値と一致したら終了です。
削除
10という要素を削除したいとします。
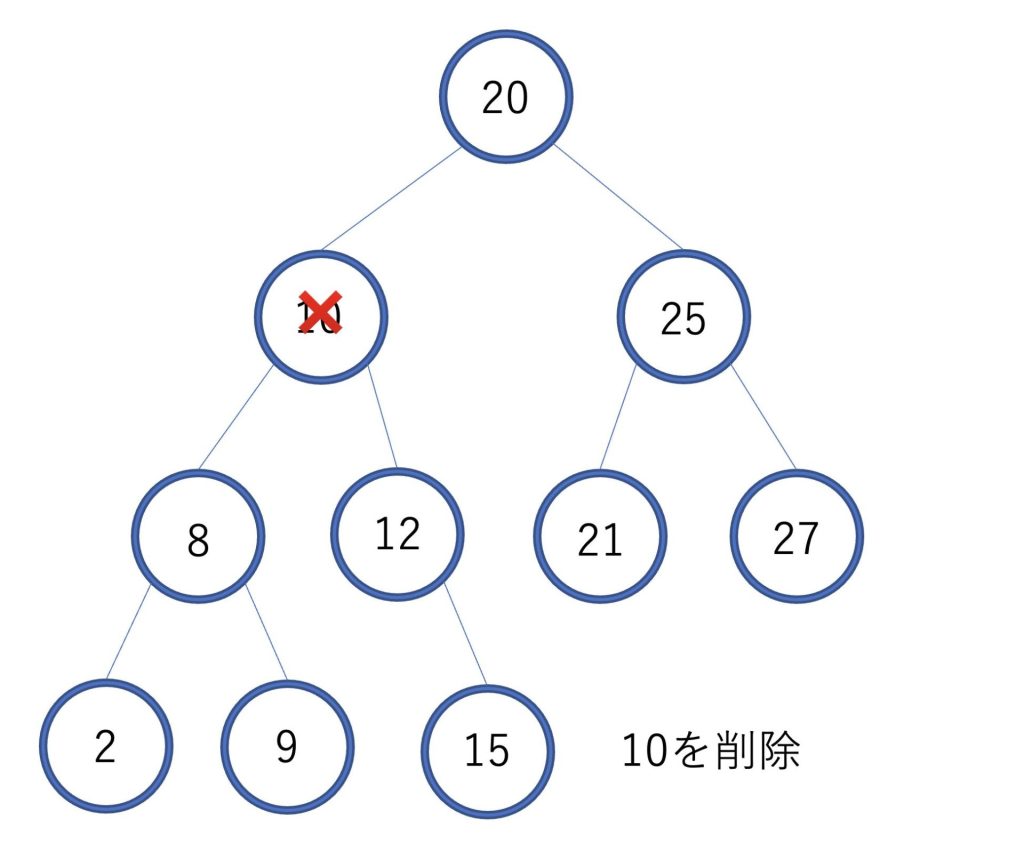
まず先ほどと同じように探索をして、10を見つけてから10を削除します。
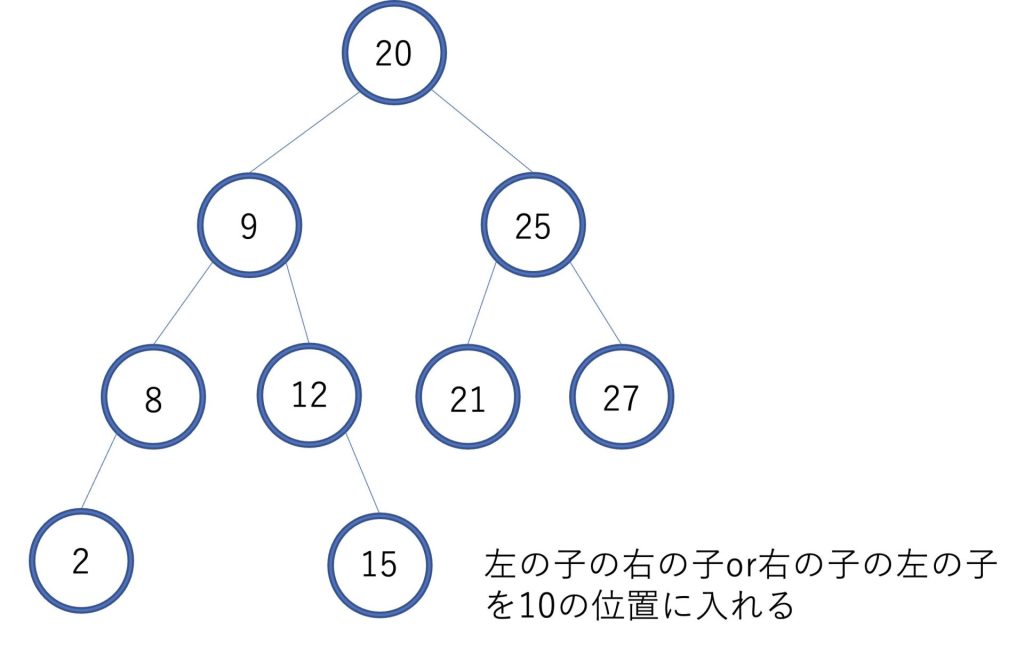
次に10があった位置の右にある要素の中で最も小さい値か、左にある要素の中で最も大きい値を10の位置に入れます。
今回は左の要素の中で最も大きい値の9を入れました。
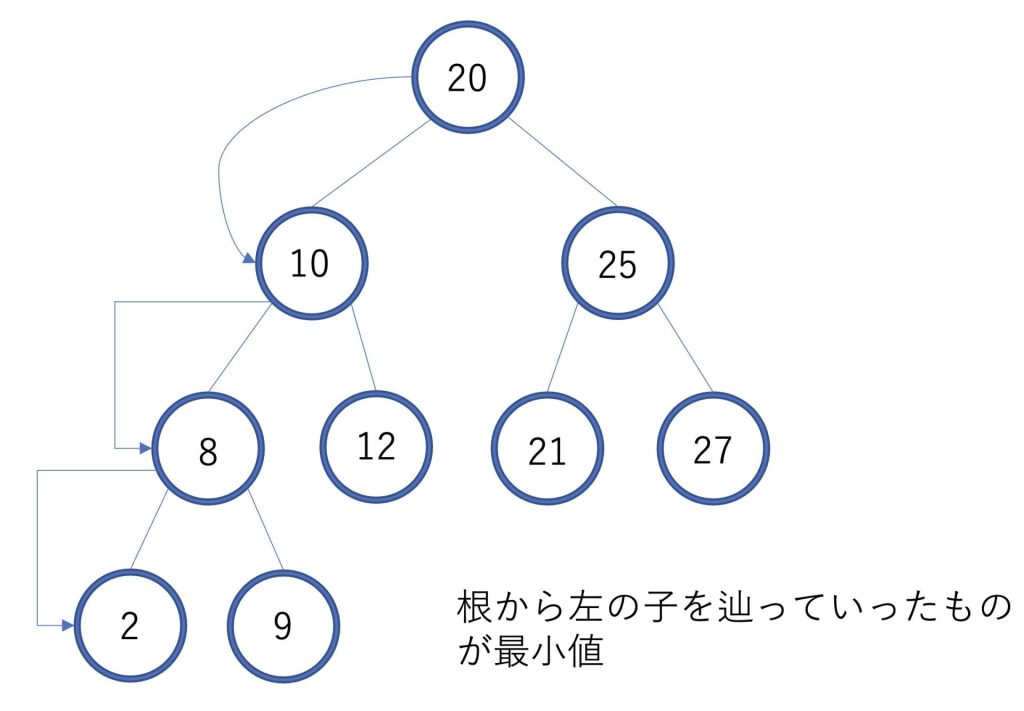
最小値の探索
最小値の探索は、左の子を辿っていくと見つけることができます。
要素がn個ある場合、二分探索木の総数は1/(n+1)2nCnとなります。(カタラン数の漸化式)
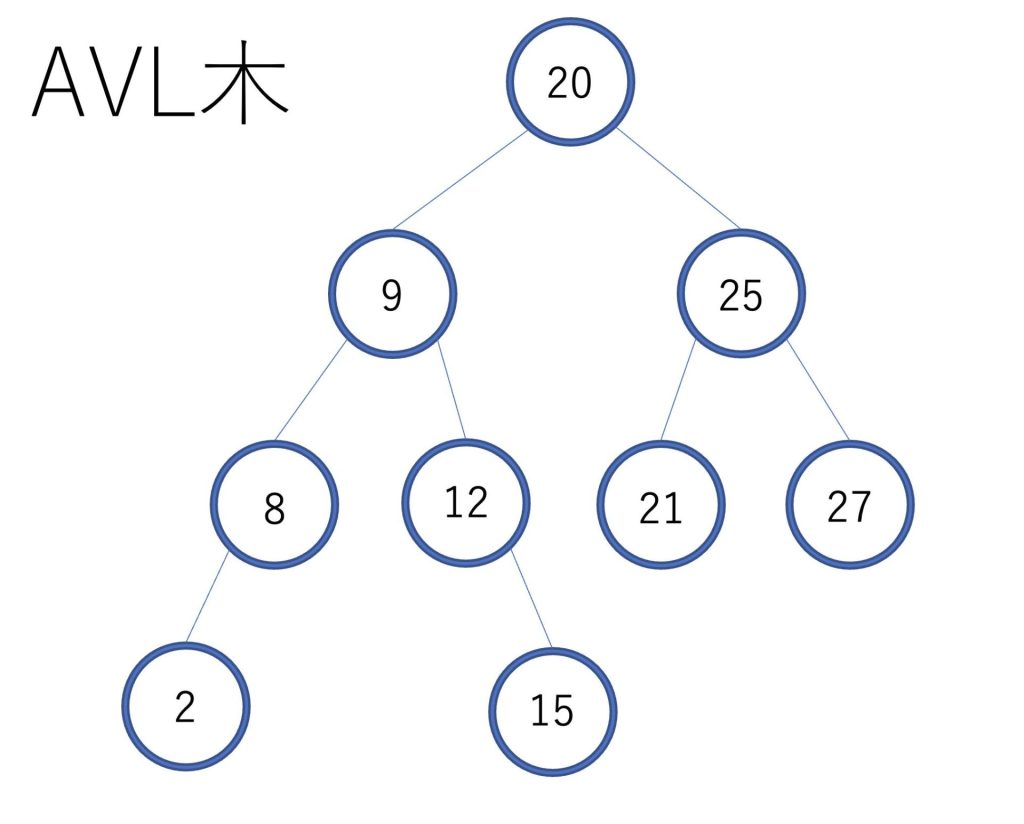
AVL木
二分探索木は挿入、削除、探索、最小値の探索の平均計算量がO(logn)になりますが、最悪計算量はO(n)になってしまいます。
これを最悪計算量もO(logn)にするために考えられたものがAVL木です。
AVL木の条件は以下です。
全ての接点において左部分木と右部分木の高さの差が1以下になっているもの
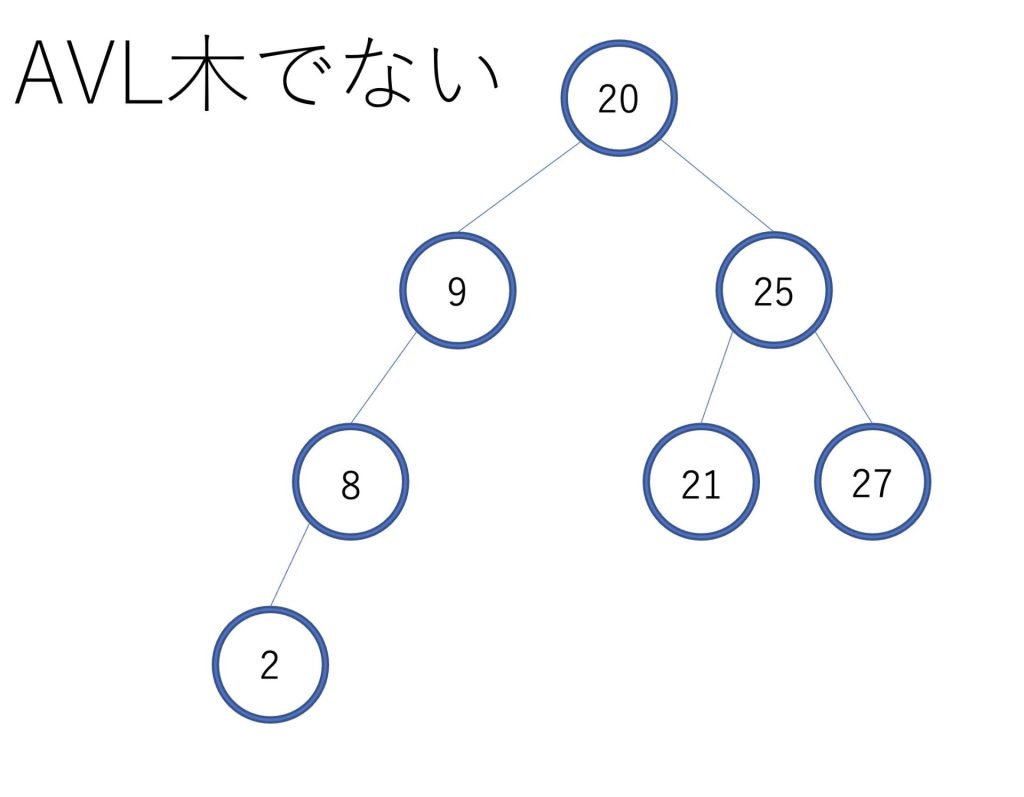
9の要素から見て左の子が高さ2であるのに対し、右の子は高さ0となっています。
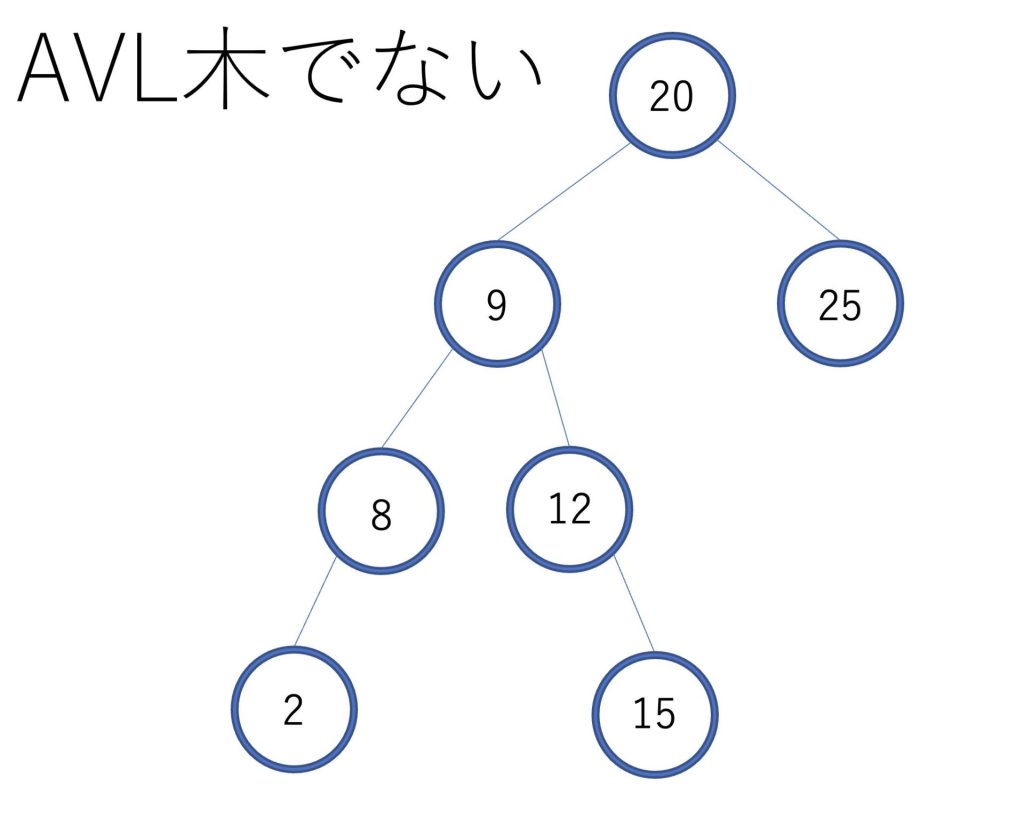
20の要素から見て左部分木の高さは3になっているのに対し、右部分木の高さは1になっています。
まとめ
・二分ヒープとは親よりも子の要素の方が大きいという条件を満たし、挿入と最小値の削除をO(logn)で行うことができる
・二分探索木とは全ての接点において左にある子が自身の数より小さく、右にある子が自身の数より大きいという条件を満たし、挿入、削除、探索、最小値の探索を平均計算量O(logn)で行うことができる
・AVL木とは、全ての接点において左部分木と右部分木の高さの差が1以下になっているもので、二分探索木の最悪計算量を改善するために考案された
アルゴリズムおすすめ書籍です。

他にもいろんな記事があるにゃ。



コメント