はじめに
こんにちは。将棋と筋トレが好きな、情報系大学生のゆうき(@engieerblog_Yu)です。
今回はニューラルネットワークの最適化問題を解く手法である、モーメンタム法についてまとめていきたいと思います。
Momentum法とは?
Momentum法は、勾配降下法に物理の慣性の法則を取り入れたようなものです。
Momentumとは「運動量」という意味を持っています。
Momentum法は以下の式で表されます。
\(v_{next} = αv_{initial} – η\frac{∂L}{∂x}\)
\(x_{next} = x_{initial} + v_{next}\)
前回の記事でも解説しましたが、勾配降下法は以下の式で表されます。
\(x_{next} = x_{initial} – η\frac{∂L}{∂x}\)
Momentum法は勾配降下法に速度を取り入れて、勾配方向に力を受けるという物理法則を表しています。
Momentum法のイメージ
式では分かりにくいと思うので図で表すと以下のようになります。
Momentum法は、傾斜がある地面をボールが転がるような動きになります。



Momentum法の数式をもう一度記述します。
\(v_{next} = αv_{initial} – η\frac{∂L}{∂x}\)
\(x_{next} = x_{initial} + v_{next}\)
αは摩擦や空気抵抗などのような、物体が減速するためのパラメータとなります。
αとηはハイパーパラメータにあたります。

それではPythonで実装していきたいと思います。
ライブラリのインポート
import numpy as np
import matplotlib.pyplot as pltMomentum法をPythonで実装
# モーメンタムクラスを実装
class Momentum:
def __init__(self,lr,momentum):
self.lr = lr
self.momentum = momentum
self.v = None
# 速度を勾配に合わせて更新する
def update(self,grad,x_initial):
if self.v is None:
self.v = 0
else:
self.v = self.momentum * self.v - self.lr * grad
# x座標を速度分だけ更新する
x_next = self.v + x_initial
return x_next今回は損失関数を\(L=(a-x)^2\)に設定します。
微分を計算することで\(\frac{∂L}{∂x}=-2(a-x)\)となるので、そちらも合わせて実装します。
# 損失関数の設定
def loss_function(x, a):
L = (a - x)**2
return L
# 勾配の計算
def calc_gradient(x, a):
grad = -2.0 * (a - x)
return grad今回はa=5とし、xの初期位置は-5にしたいと思います。
xを更新して、最終的にxの位置を5にすることが目標です。
# 損失関数のパラメータ
a = 5
# xの初期値
x_initial = -5
# 損失値
L = loss_function(x_initial, a)
# 損失関数をプロットする
x_line = np.linspace(-10, 20) # -10から10に引かれたx軸
L_line = loss_function(x_line, a)
plt.figure(figsize=(6,6))
plt.plot(x_line, L_line)
plt.xlabel('parameter x')
plt.ylabel('loss function L')
# 現在の x と損失値をプロット
plt.scatter(x_initial, L, color='r')
plt.xlim([-10, 20])
plt.ylim([-5, 200])
plt.show()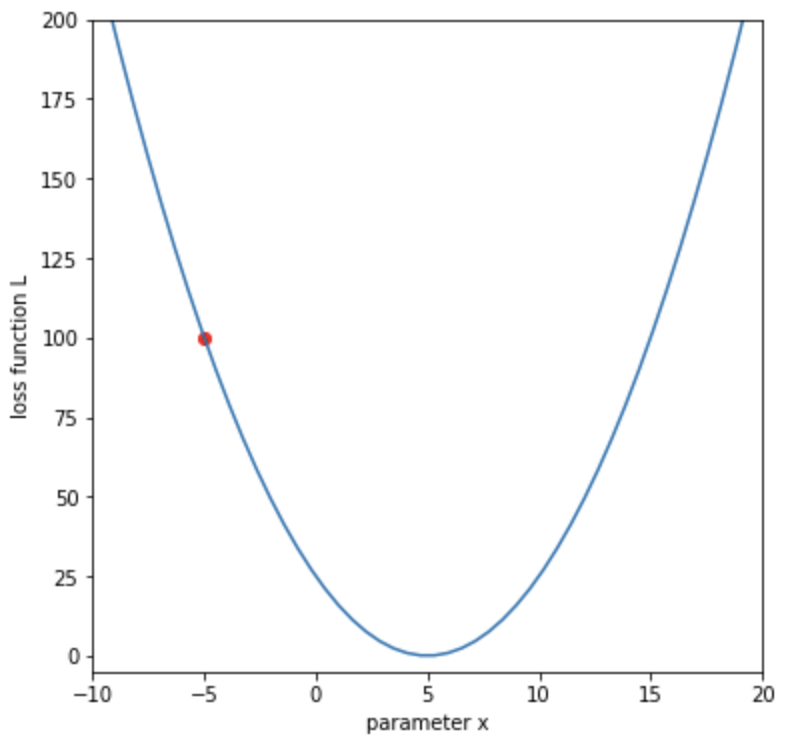
from matplotlib import animation, rc
from IPython.display import HTML
# 学習率(lr = learning rate)
lr = 0.2
# 摩擦や空気抵抗を考慮
momentum = 0.8
# Momentumオブジェクトの宣言
m = Momentum(lr,momentum)
# 更新回数
num_iterations = 50
# 初期値をコピー
x = x_initial
# 描画
fig = plt.figure(figsize=(6,6))
plt.plot(x_line, L_line)
images = []
for n in range(num_iterations):
# 損失値を計算
L = loss_function(x, a)
# 勾配を計算
grad = calc_gradient(x, a)
print("%d-th iteration, x=%.3f, loss: %.3f, grad: %.3f" % (n, x, L, grad))
# 更新前の状態を描画
tangent = grad * (x_line - x) + L
img = plt.plot(x_line, tangent, color='r')
img.append(plt.scatter(x, L, color='r'))
img.append(plt.text(-8, 180, 'iteration: '+str(n), size='x-large'))
images.append(img)
# 更新
x = m.update(grad,x)
plt.xlim([-10, 20])
plt.ylim([-5, 200])
plt.xlabel('parameter x')
plt.ylabel('loss function L')
# アニメーション作成
anim = animation.ArtistAnimation(fig, images, interval=100)
# Google Colaboratoryの場合必要
rc('animation', html='jshtml')
plt.close()
display(anim)ボールが転がるように、損失関数が最小化していくことがわかります。
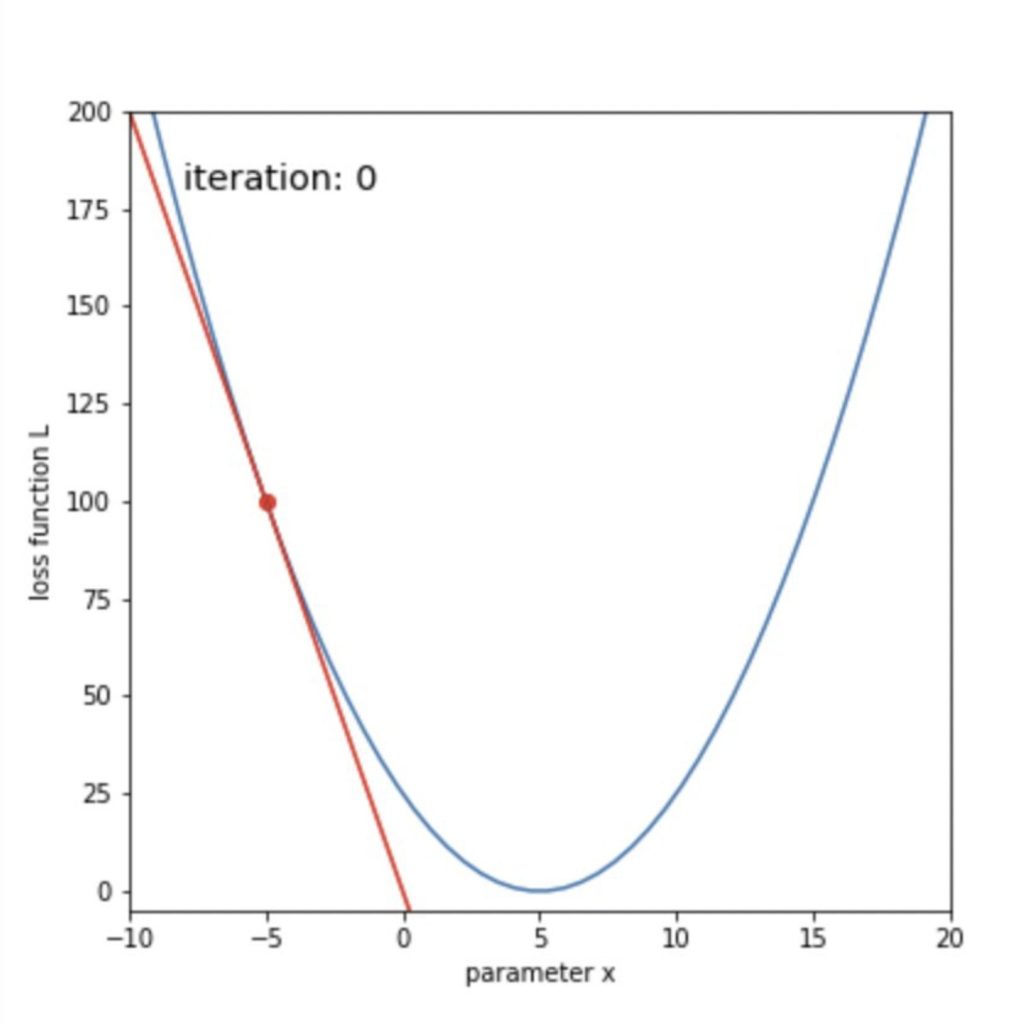
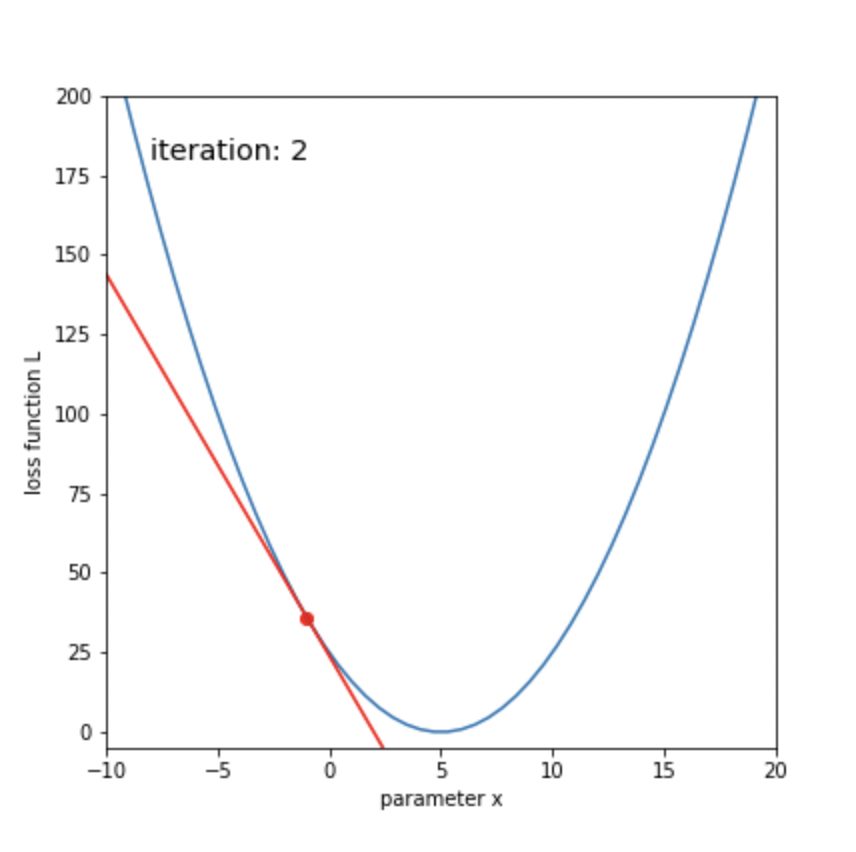
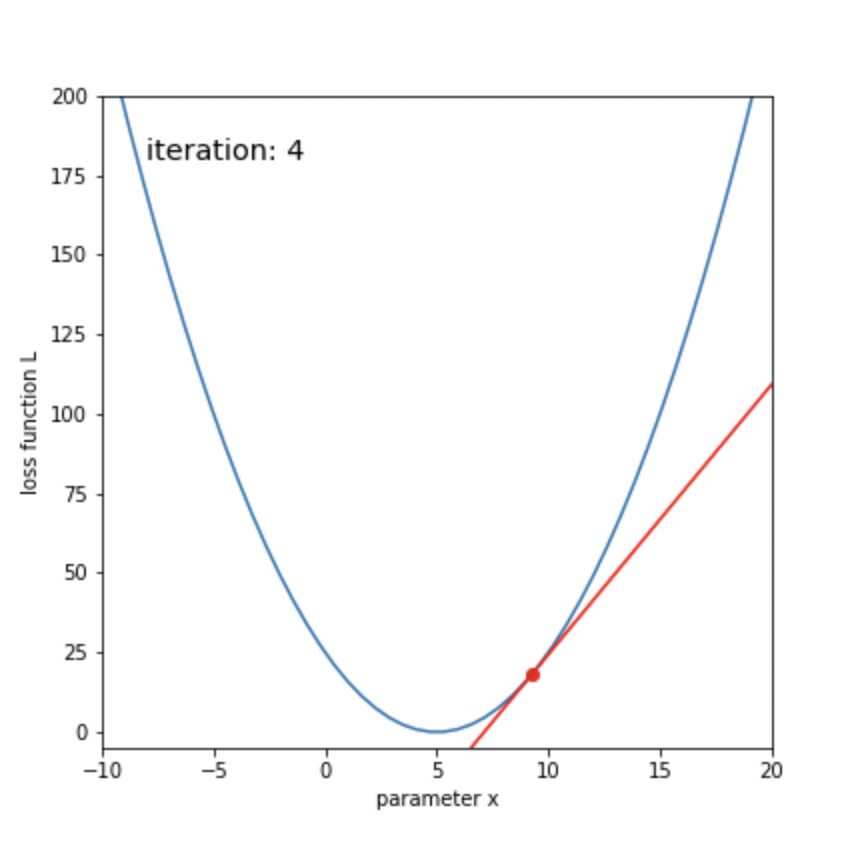
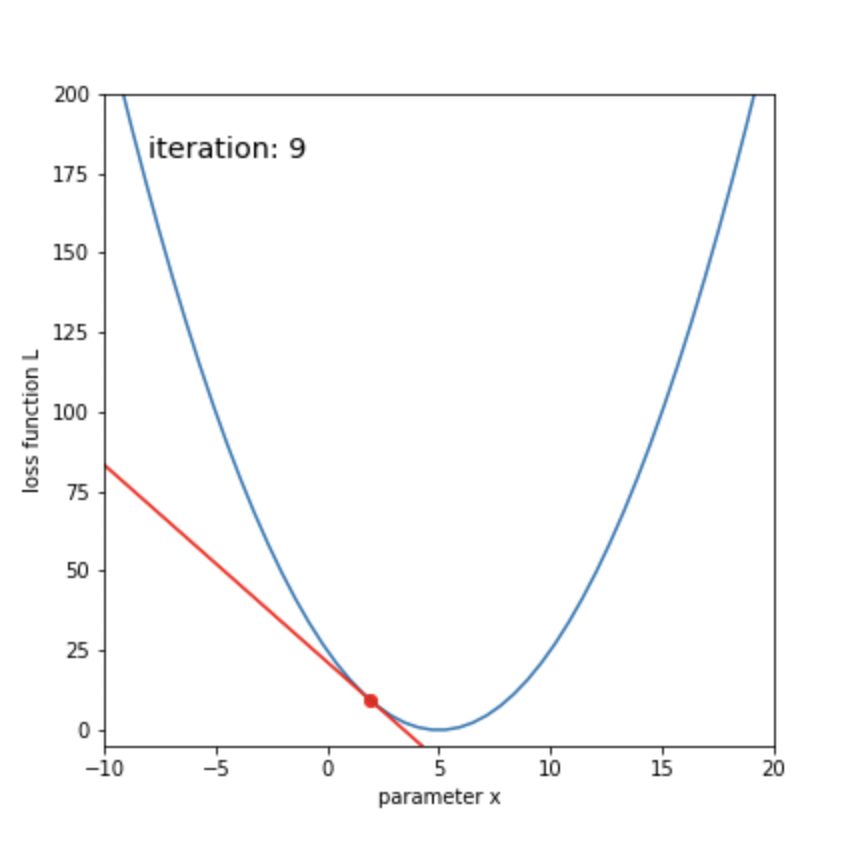
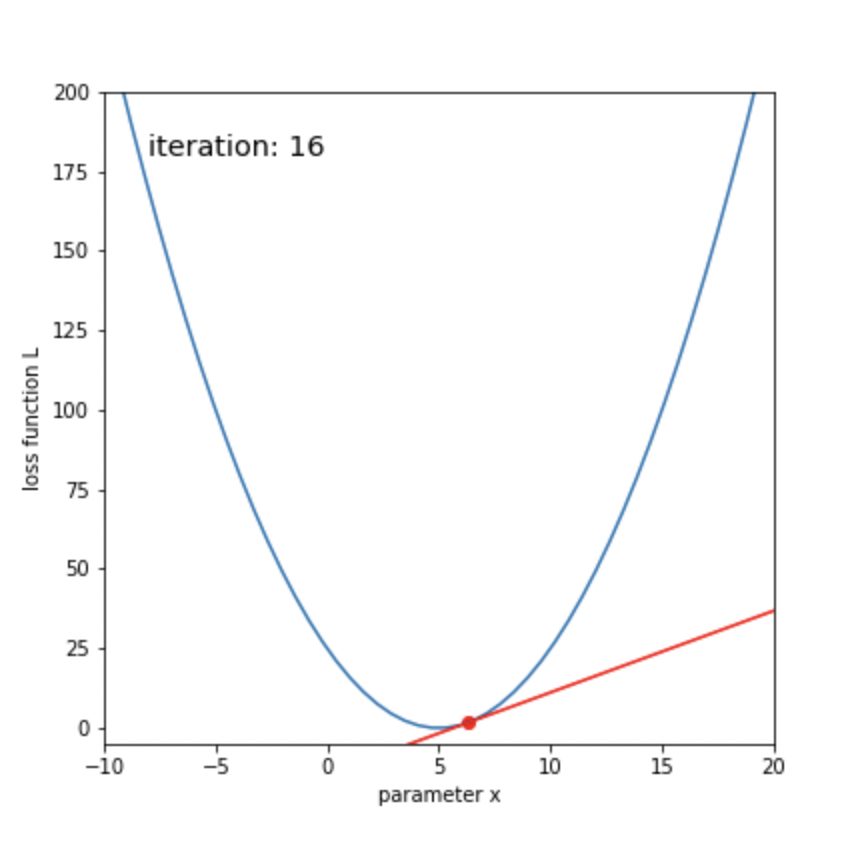
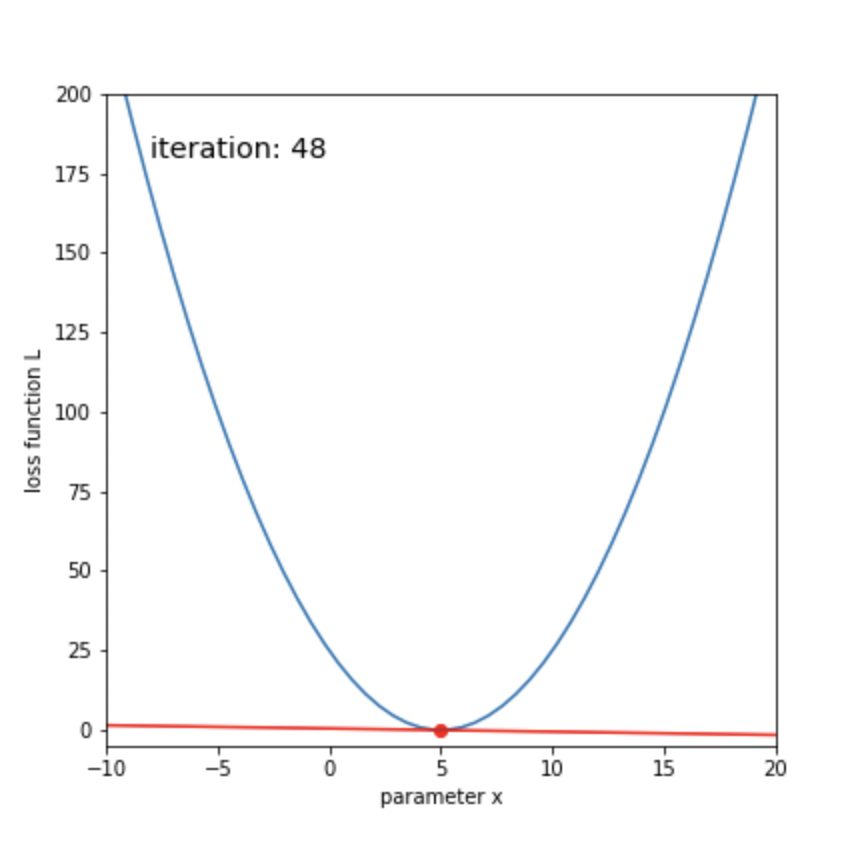
50回ほどの更新で、xが目標の5に辿り着いたことがわかります。
まとめ
Momentum法とは、勾配方向に速度を取り入れたもので、ボールが転がるようなイメージ
\(v_{next} = αv_{initial} – η\frac{∂L}{∂x}\)
\(x_{next} = x_{initial} + v_{next}\)
αとηはハイパーパラメータ
今回はニューラルネットワークのMomentum法についてまとめました。
機械学習、ディープラーニングを学びたい方におすすめの入門書籍です。
ディープラーニングの理論が分かりやすくまとめられていて、力を身につけたい方におすすめです。

最後まで読んでいただきありがとうございました。

他にもいろんな記事があるにゃ。



コメント