どーも、情報系大学生のゆうき(@engieerblog_Yu)です。
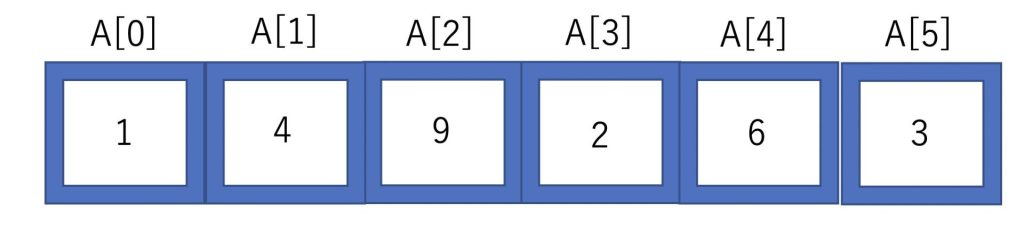
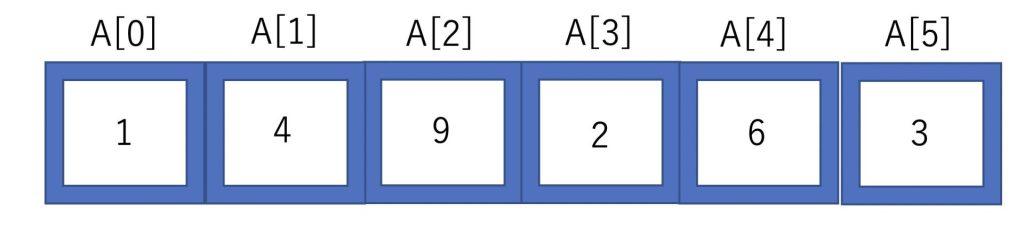
今回はこのような配列を昇順(小さい順)に並び替えていくことを考えましょう。
みなさんはどのように整列しようと考えるでしょうか?
整列の方法はいろいろありますが、計算量の観点でどのような整列アルゴリズムを選ぶかが大切になってきます。
今回はその中のヒープソートをまとめていきたいと思います。
過去の記事も併せてどうぞ。
まずはヒープソートに使われる二分ヒープについてです。
二分ヒープについて
二分ヒープは以下の条件を満たします。
親ノードよりも子ノードの方が値が大きい
広義の完全二分木になっている(全ての葉が左詰めになっている)
(親ノードよりも子ノードが小さいものとして二分ヒープを構成している場合もあります。)
二分ヒープは主に、挿入と最小値の削除を効率的に実行することができます。
詳しくはこちらの記事で解説しています。
ヒープソートは二つのフェーズに分かれます。
ヒープの初期化
最大値の削除
それでは、先ほどの配列をヒープソートを使って昇順にソートしていきたいと思います。
ヒープの初期化(前半フェーズ)
先ほどの配列をヒープで表すと以下のようになります。
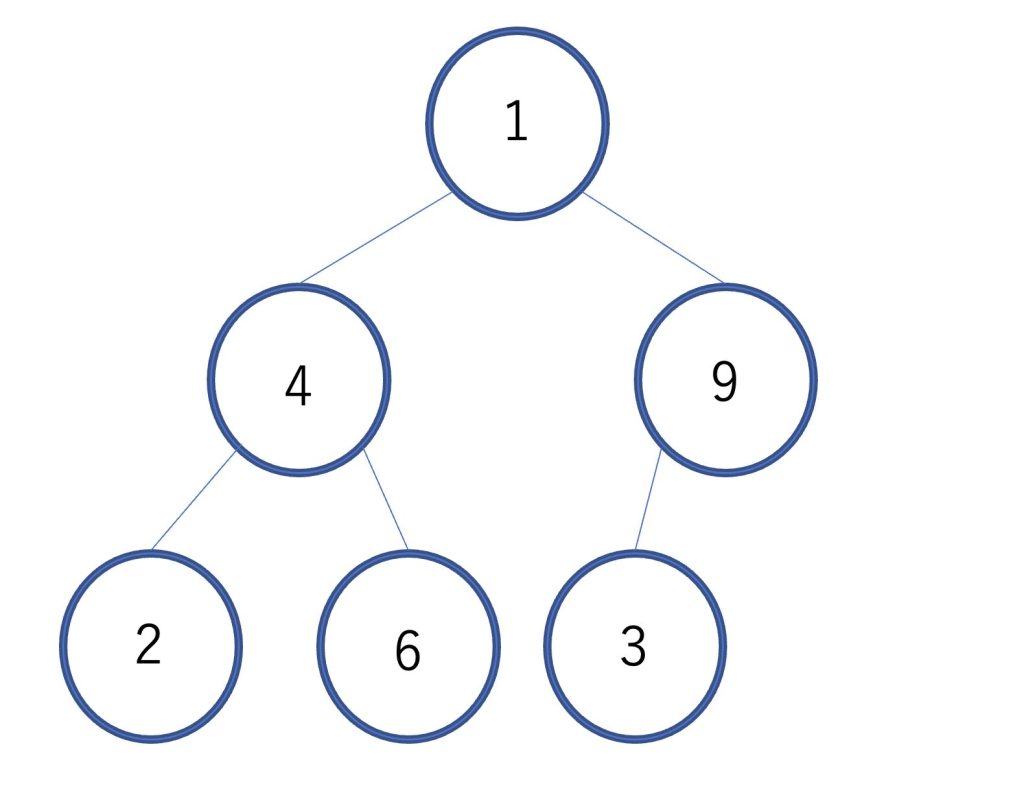
配列の後ろにある要素から、ヒープの初期化を行なっていきます。
ヒープの初期化とは親が子よりも大きい値を持つヒープを構成することです。
今回は9、4、1の順番で値を交換していくことになります。
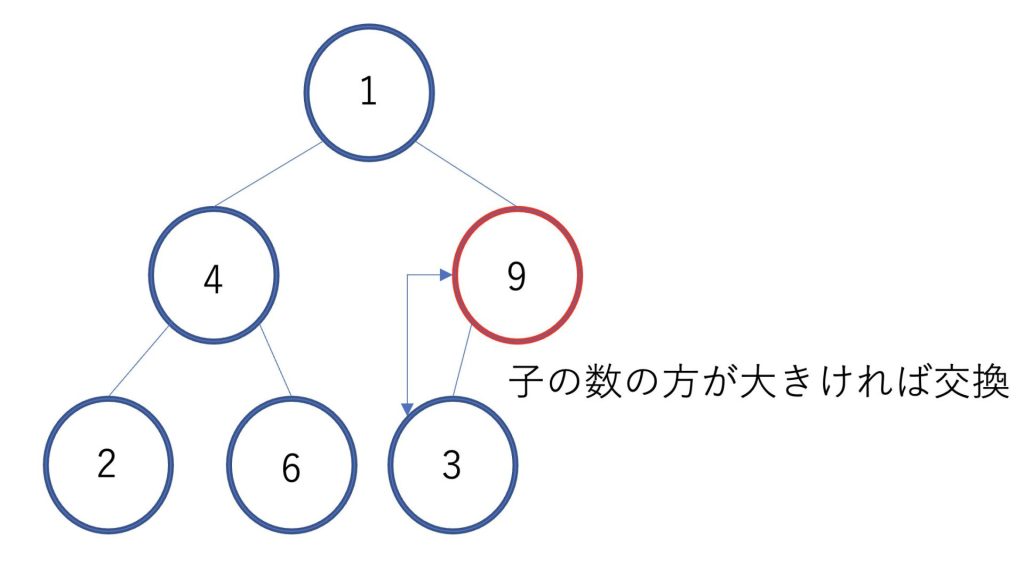
9と3は9の方が大きいのでそのままです。
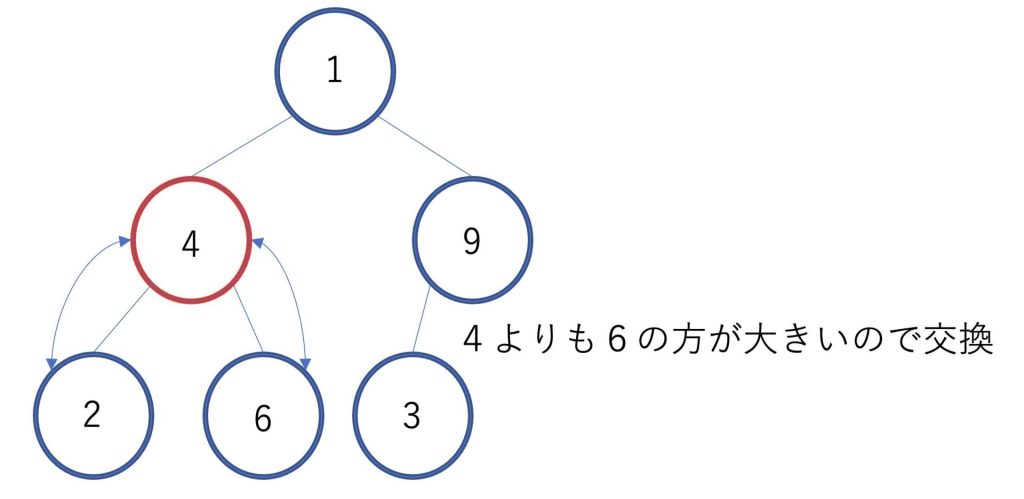
次に4を見ると、4と2と6で6が一番大きいので4と6を交換します。
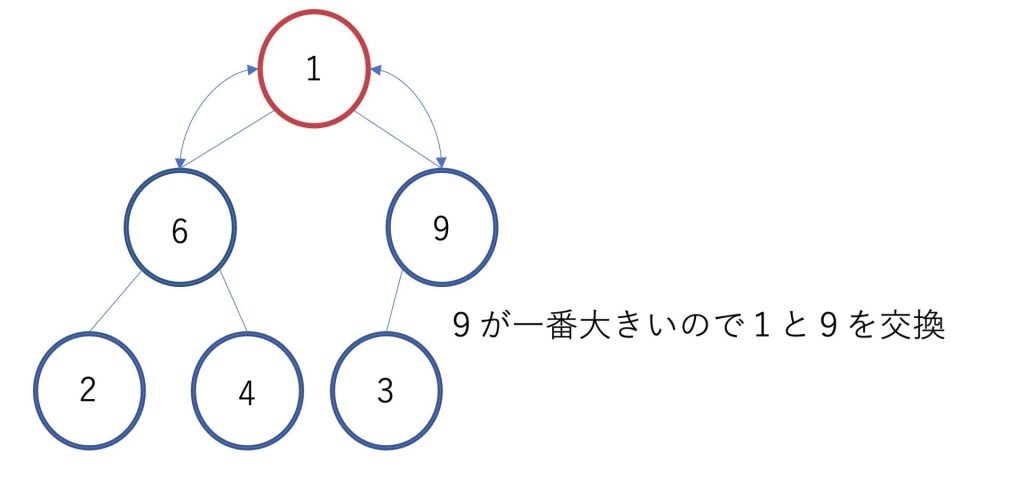
最後に1を見ると1と6と9の中で9が一番大きいので1と9を交換します。
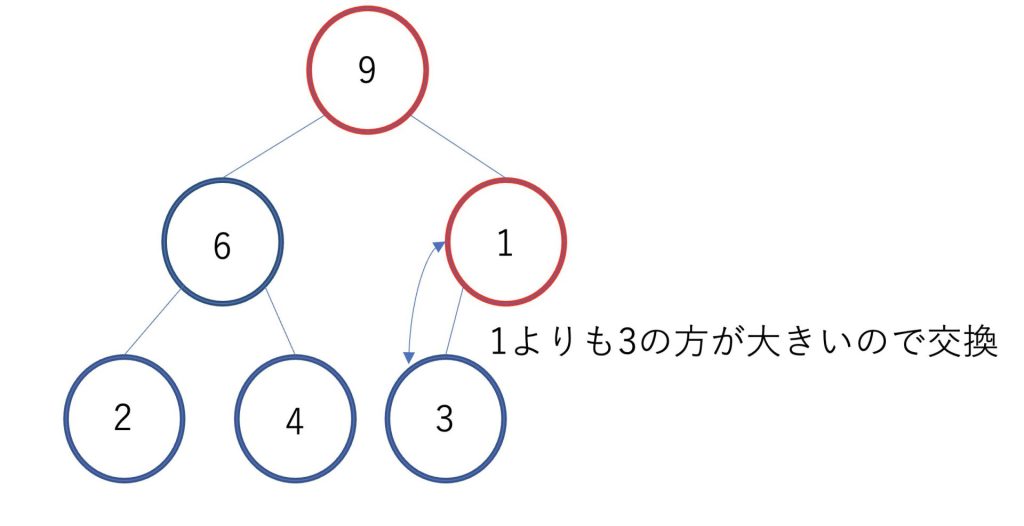
1と9を交換した時に3の方が1より大きいので交換します。(忘れがちです)
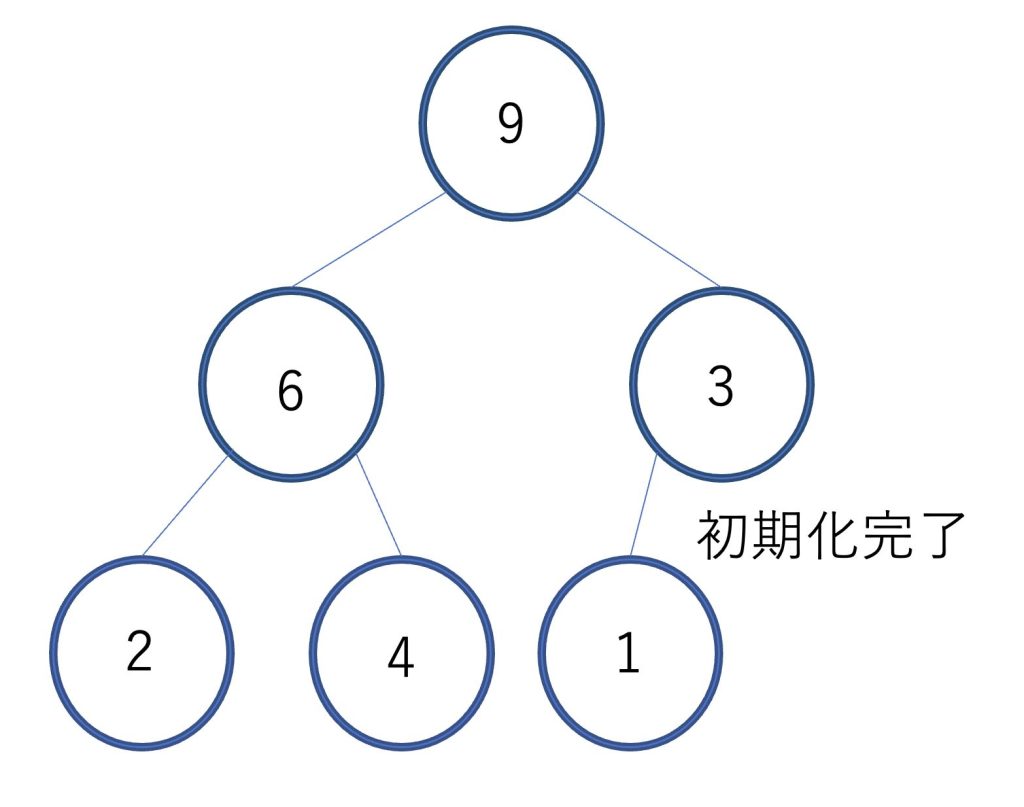
ヒープの条件を満たすことができていることがわかります。
ヒープの初期化の計算量はO(n)となります。
最大値の削除(後半フェーズ)
次に最大値を削除していきます。
最大値の削除では以下のことを行います。
1.根の値を配列の一番後ろに格納する
2.ヒープの一番後ろの要素を根に移動する
3.ヒープ条件を満たすように、ヒープを再構築する
4.ヒープの要素がなくなるまで繰り返す
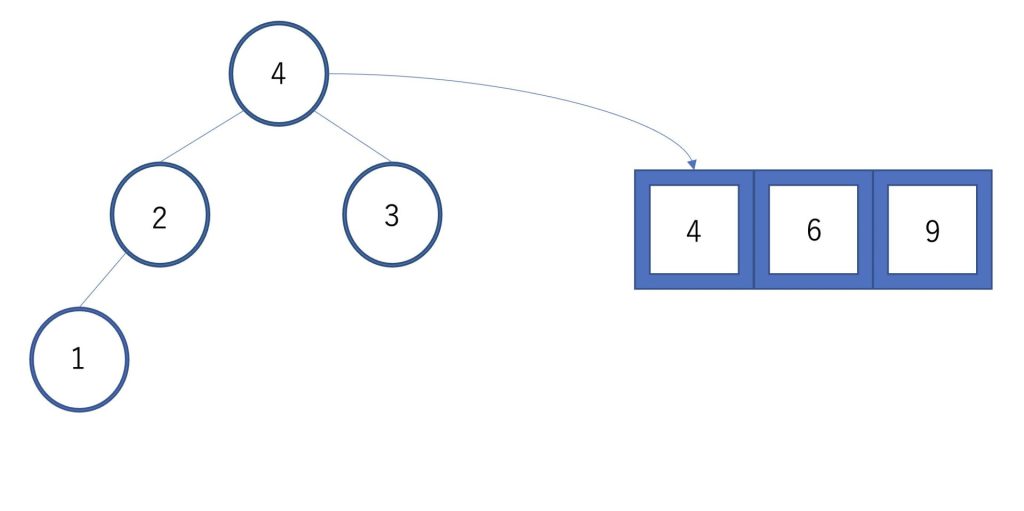
まず根にある9を配列の一番後ろに移動します。
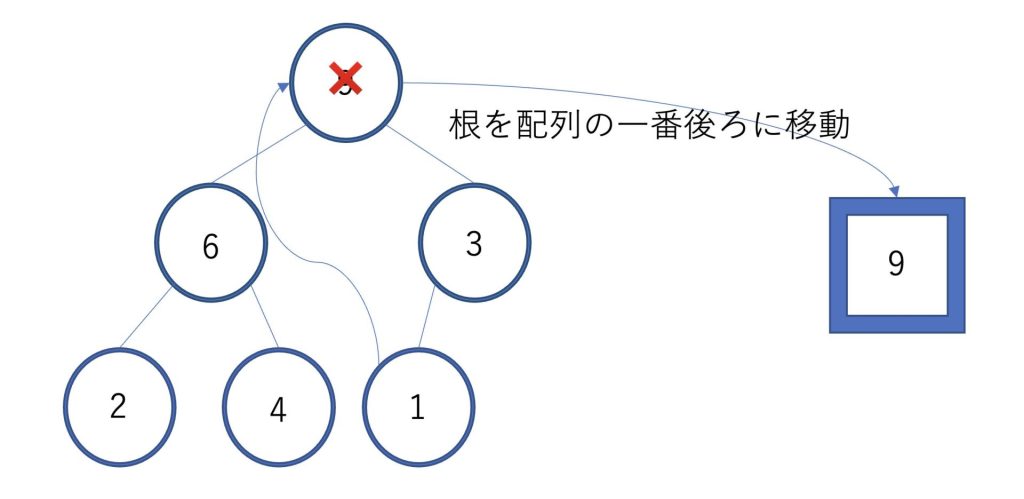
ヒープの一番後ろにある1が根に交換されます。
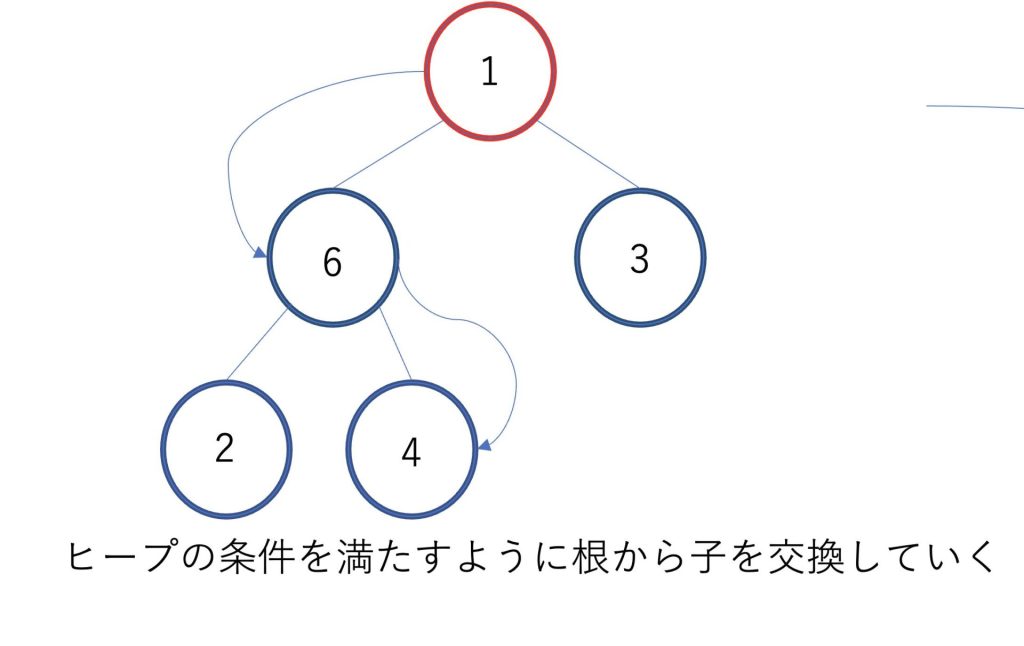
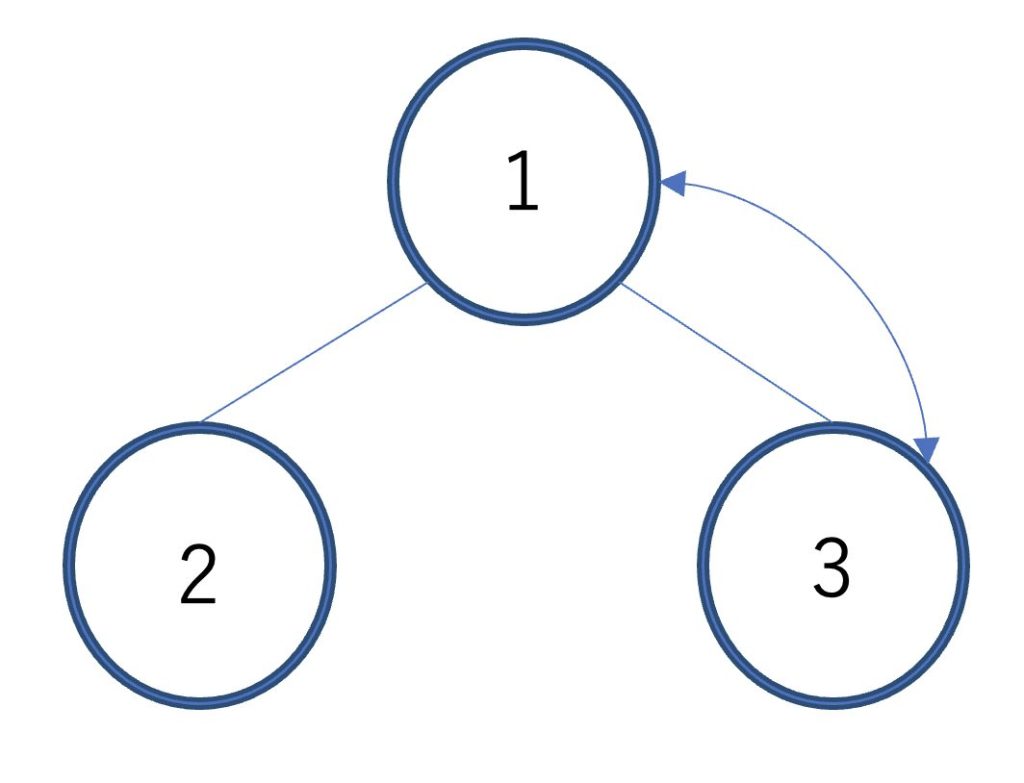
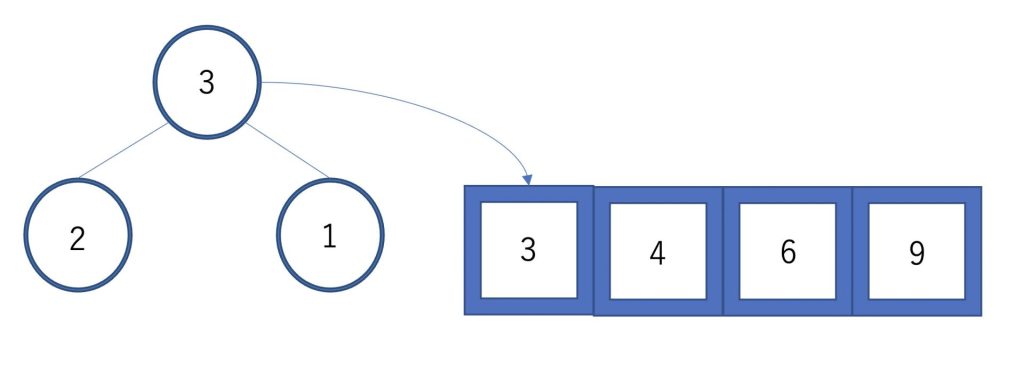
ヒープの条件が満たされていることが確認できたら、次は6を配列に移動します。
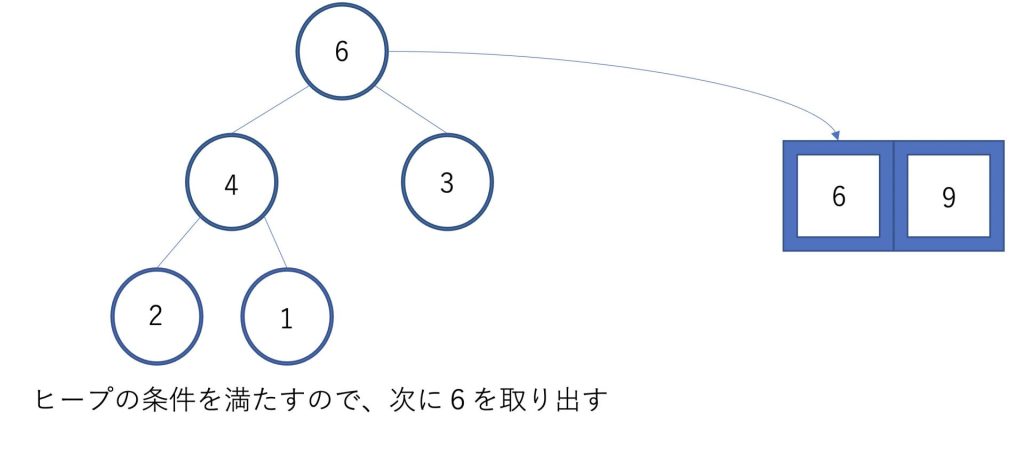
ヒープの一番後ろにある要素を根と交換して、同じ操作を繰り返していきます。
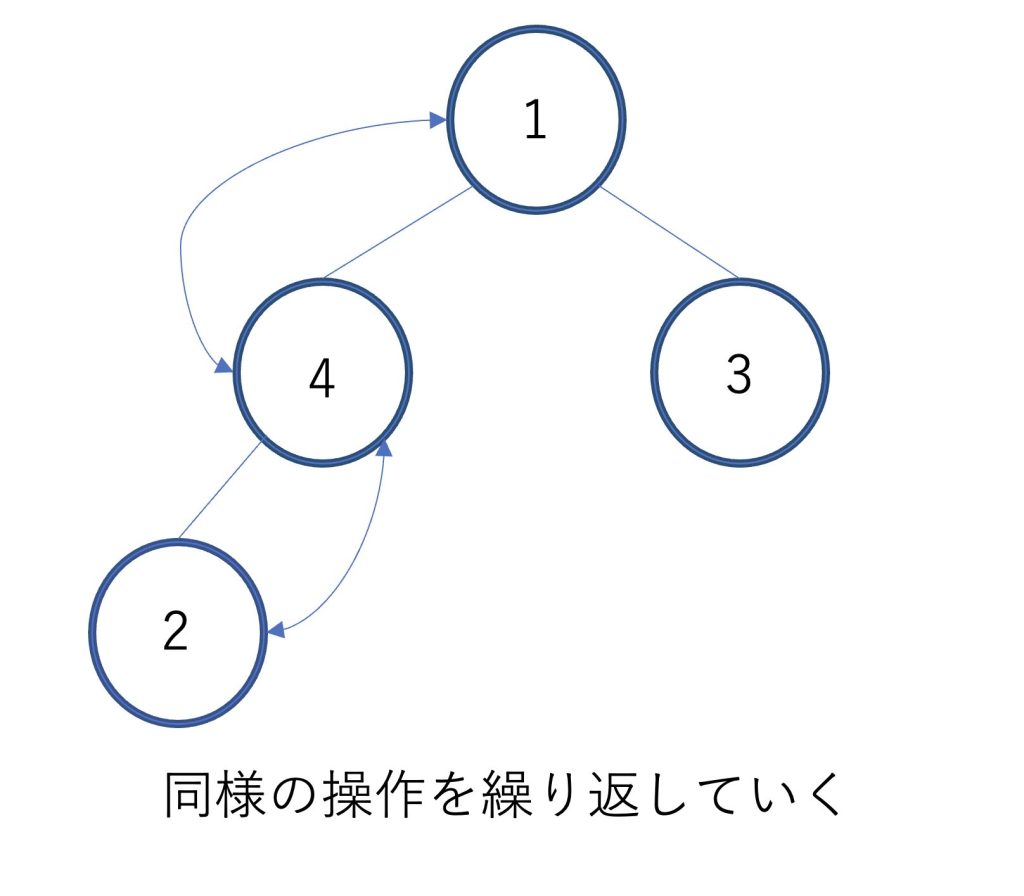
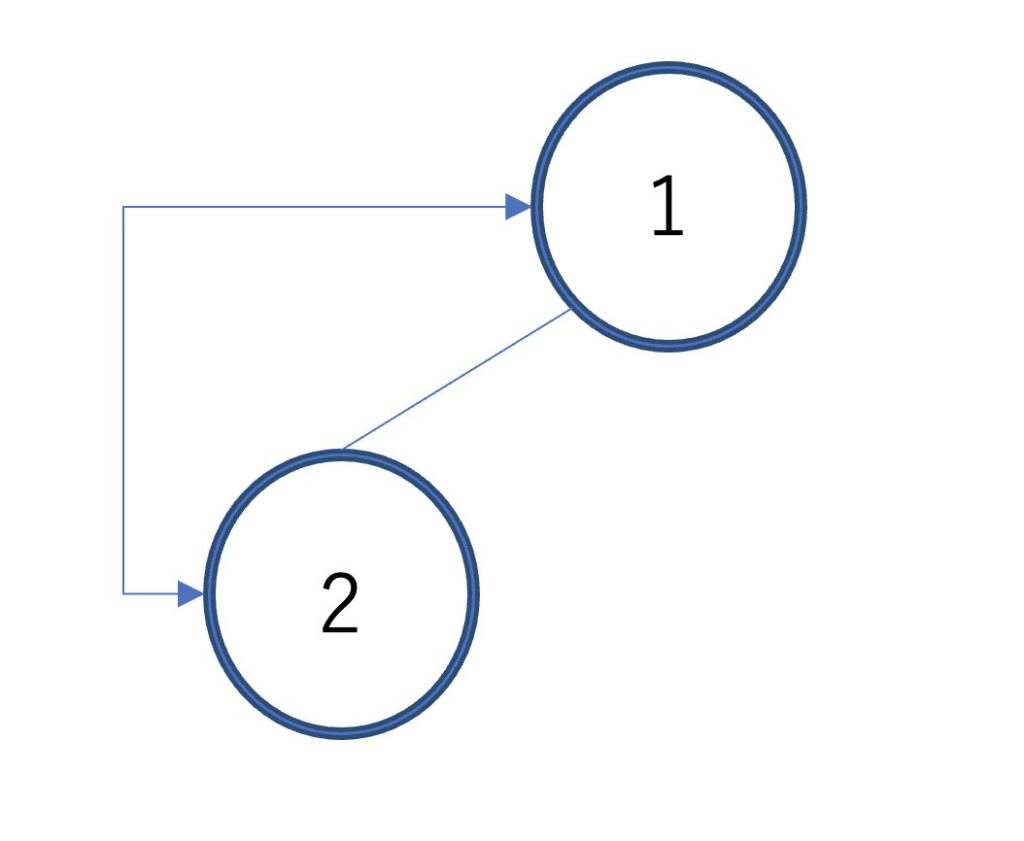
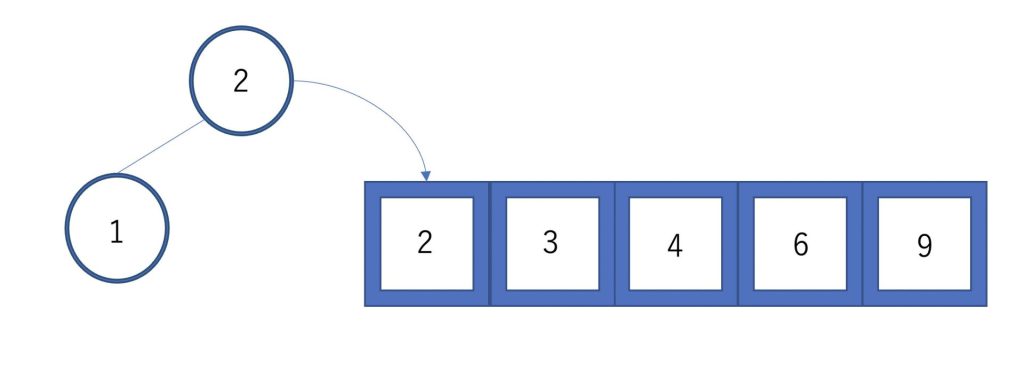
最後に1が残るのでA[0]に移動してあげれば昇順にソートすることができます。
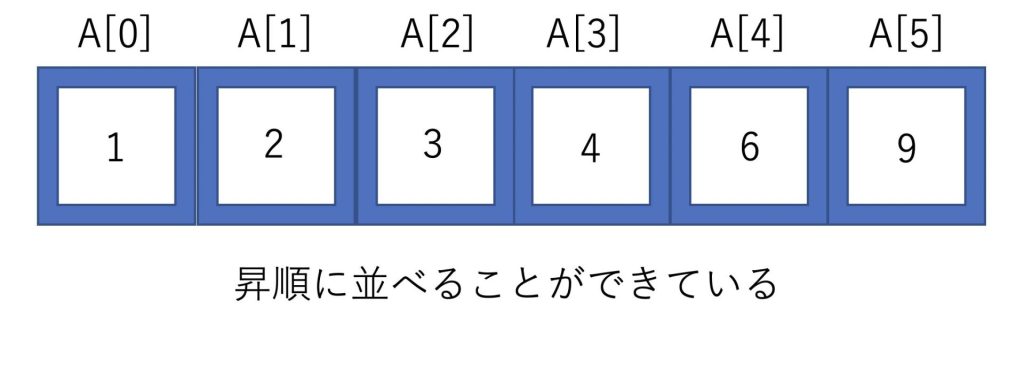
最大値の削除の計算量はO(nlogn)となります。
またそれにより全体の計算量はO(nlogn)になります。
ヒープソートの計算量はO(n)+O(nlogn)=O(nlogn)となる
まとめ
ヒープソートはヒープの初期化と最大値の削除により行われる
計算量はO(nlogn)となる
アルゴリズムの勉強におすすめの書籍です。

整列アルゴリズムの計算量はO(nlogn)よりも小さくことはできないと証明されているので、極めて優秀なアルゴリズムと言うことができます。

いろんな投稿があるにゃ。






コメント