初めに
こんにちは。将棋と筋トレが好きな、学生エンジニアのゆうき(@engieerblog_Yu)です。
今回はニューラルネットワークのモデルの学習に使われる勾配降下法についてまとめていきたいと思います。
勾配降下法について
ニューラルネットワークのモデル学習では、重みとバイアスを最適化していきます。
重みとバイアスを最適化するために、損失関数を考えます。
損失関数の値が最も小さくなったときに、重みとバイアスが最適になっているということができます。
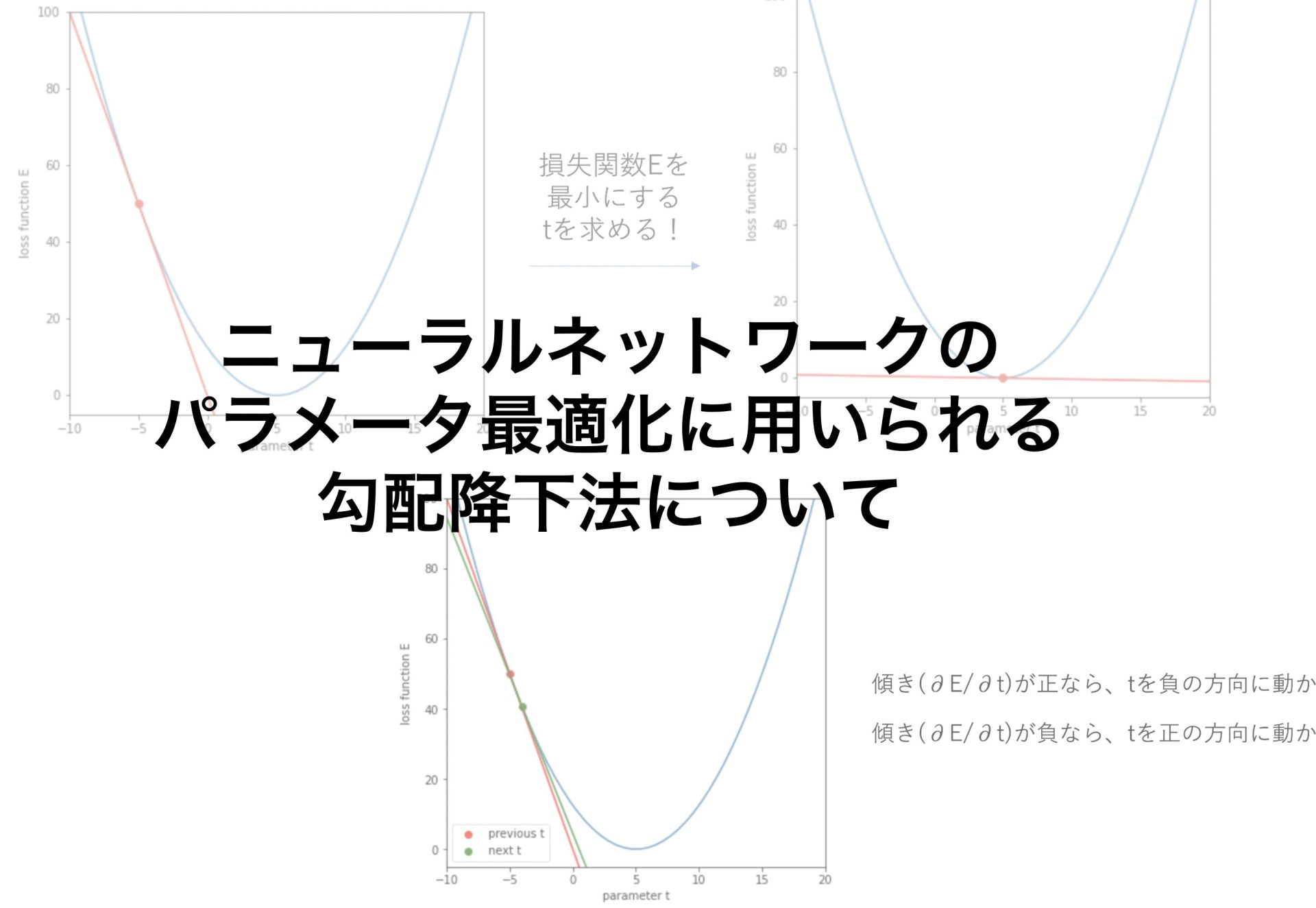
勾配を利用して、損失関数が最小になるパラメータを探索しようとしたものが勾配降下法です。
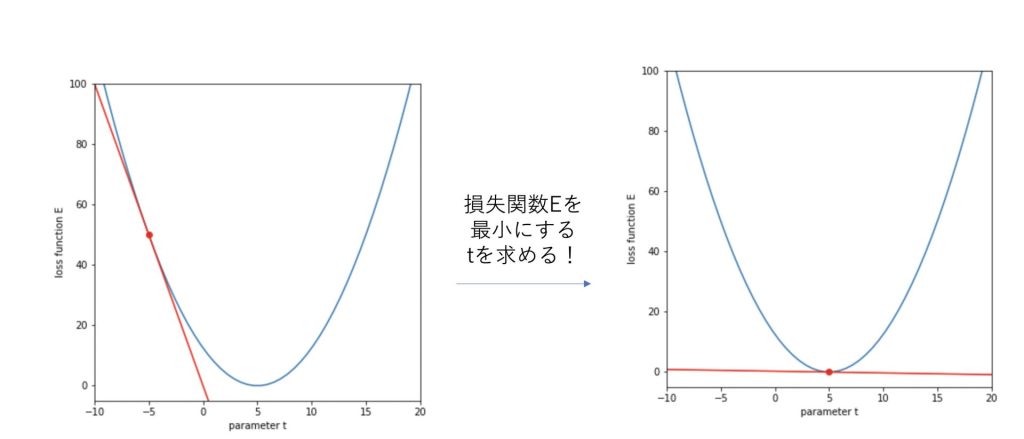
勾配降下法は
\(t_{next}=t_{previous} – \eta\frac{\partial E}{\partial t}\)
と表されます。
式で見ると分かりにくいので図で表してみます。
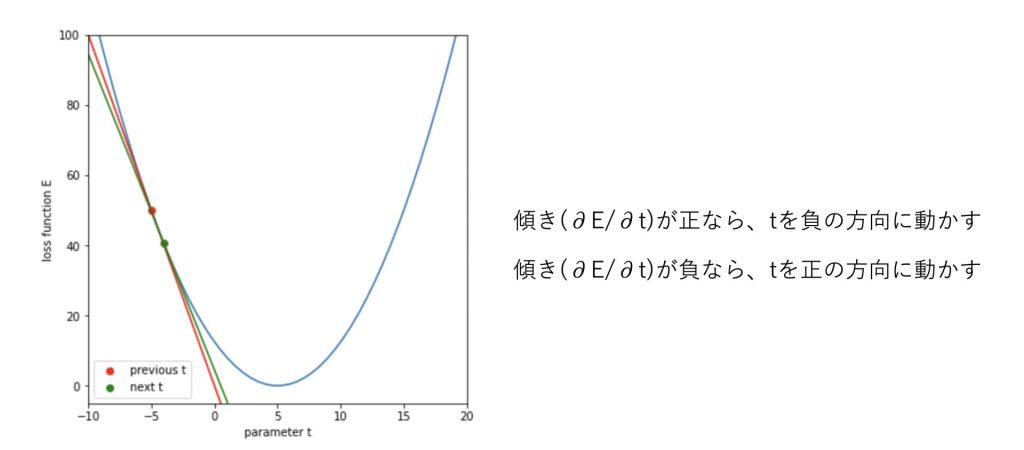
傾きに応じてtを適切な方向に動かすと、tが最適な値(今回は5)に近づいていくことがわかるはずです。
学習率について
学習率はηで表されています。
ηは人間が設定するもの(ハイパーパラメータ)で一般に大きければ良いというものではなく、適切な値に設定する必要があります。
学習率が大きいと収束が早くなるように思えるかもしれませんが、実際には振動を起こしてしまい学習がストップしてしまうということがあり得ます。
学習率はハイパーパラメータであり、適切な値に設定する必要がある
Pythonで勾配降下法を実装
それでは勾配降下法を実装していきたいと思います。
# ライブラリのインポート
import numpy as np
import matplotlib.pyplot as plt今回は、損失関数を二乗誤差にして実装していきます。
\(E=\frac{1}{2}(y-t)^2\)
# 損失関数(二乗誤差)
def squared_error(t, y):
return 0.5*(y - t)**2まずは、tの初期値を設定して、グラフ表示してみます。
今回は勾配降下法を用いて、tを5に近づけていきましょう。
(今回は単純化しているため目標が5とわかりますが、実際にはこの値はわかりません。)
# 損失関数のパラメータ
a = 5
# tの初期値を設定
t_initial = -5
# 損失値を求める
E = squared_error(t_initial, a)
print('loss = ' + str(E))
# 損失関数をプロットする
t_line = np.linspace(-10, 20)
E_line = squared_error(t_line, a)
plt.figure(figsize=(6,6))
plt.plot(t_line, E_line)
plt.xlabel('parameter t')
plt.ylabel('loss function E')
# 現在の t と損失値をプロット
plt.scatter(t_initial, E, color='r')
plt.xlim([-10, 20])
plt.ylim([-5, 100])
plt.show()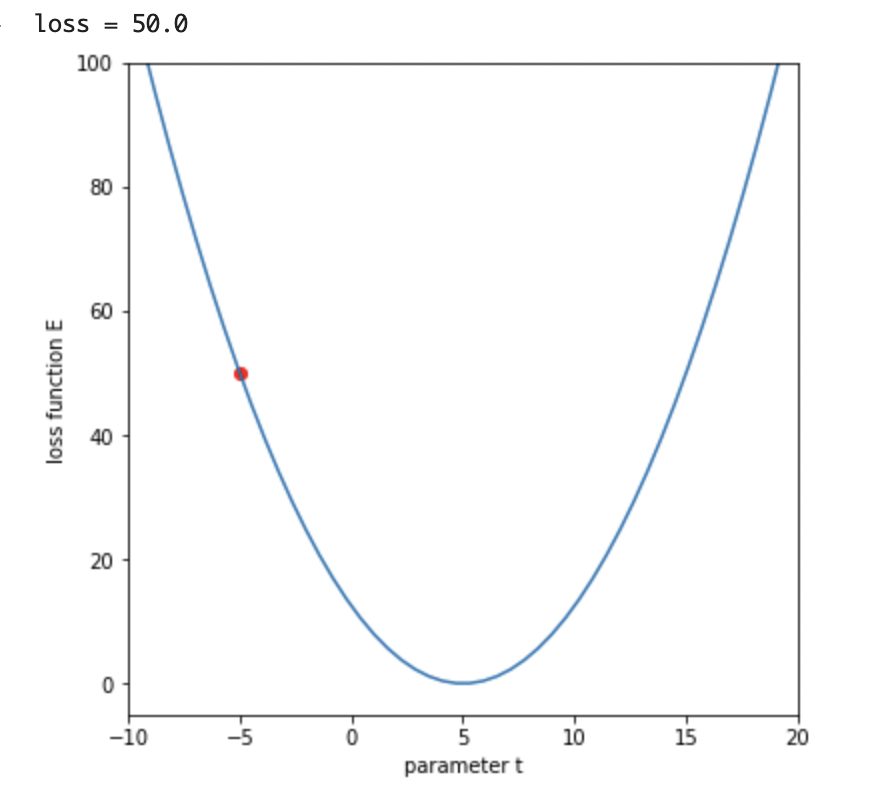
今回の勾配は微分すると
\(\frac{\partial E}{\partial t} = -(y-t)\)
となるので、勾配を計算する関数を実装します。
# 勾配の計算
def calc_gradient(t, y):
grad = -(y - t)
return gradtの初期値での接線を描画してみます。
grad = calc_gradient(t_initial, a)
# 損失関数をプロットする
t_line = np.linspace(-10, 20) # -10から10に引かれたx軸
L_line = squared_error(t_line, a)
plt.figure(figsize=(6,6))
plt.plot(t_line, L_line)
plt.xlabel('parameter t')
plt.ylabel('loss function E')
# 現在の t と損失値 E をプロット
plt.scatter(t_initial, E, color='r')
# 接線を引く
tangent = grad * (t_line - t_initial) + E
plt.plot(t_line, tangent, color='red')
plt.xlim([-10, 20])
plt.ylim([-5, 100])
plt.show()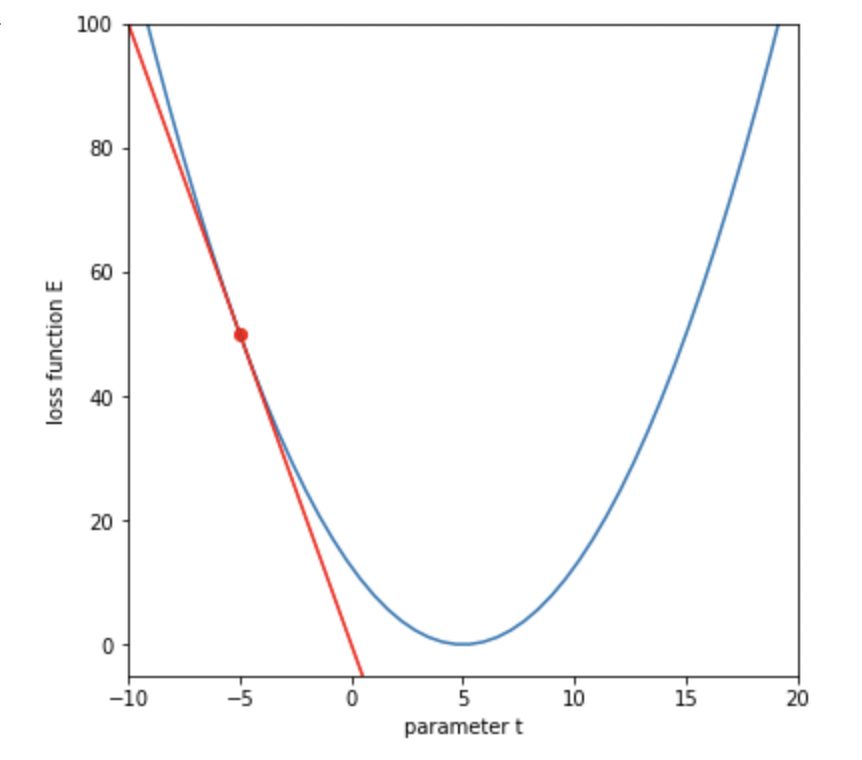
\(t=t – \eta\frac{\partial E}{\partial t}\)
先ほどの式を用いてtを更新していきたいと思います。
# 学習率
lr = 0.1
# 勾配を使って t を更新
t_next = t_initial - lr * grad
# 更新後の損失値
E_next = squared_error(t_next, a)
# 更新後の勾配
grad_next = calc_gradient(t_next, a)
plt.figure(figsize=(6,6))
# 損失関数をプロット
plt.plot(t_line, E_line)
# 一つ前の t と損失値
plt.scatter(t_initial, E, color='r', label='previous t')
# 一つ前の接線
tangent = grad * (t_line - t_initial) + E
plt.plot(t_line, tangent, color='r')
# 更新後の t と損失値と接線
plt.scatter(t_next, E_next, color='g', label='next t')
tangent_next = grad_next * (t_line - t_next) + E_next
plt.plot(t_line, tangent_next, color='g')
plt.xlabel('parameter t')
plt.ylabel('loss function E')
plt.xlim([-10, 20])
plt.ylim([-5, 100])
plt.legend()
plt.show()更新後のtでの接線が緑になります。
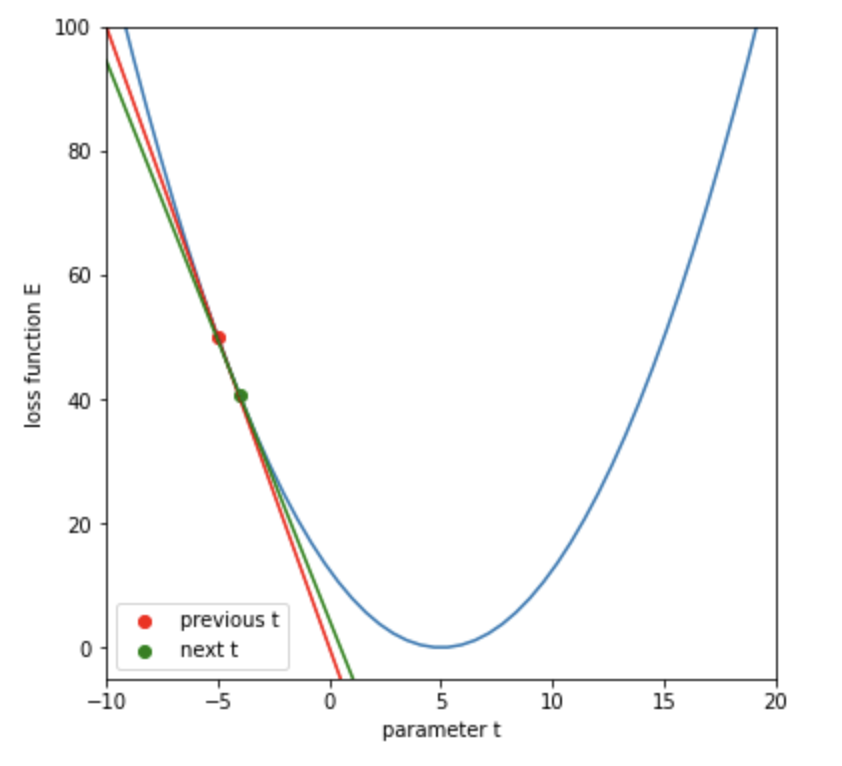
それでは更新処理を50回繰り返してみます。
from matplotlib import animation, rc
from IPython.display import HTML
# 学習率(lr = learning rate)
lr = 0.1
# 更新回数
num_iterations = 50
# 初期値をコピー
t = t_initial
# 描画
fig = plt.figure(figsize=(6,6))
plt.plot(t_line, E_line)
images = []
for n in range(num_iterations):
# 損失値を計算
E = squared_error(t, a)
# 勾配を計算
grad = calc_gradient(t, a)
print("%d-th iteration, t=%.3f, loss: %.3f, grad: %.3f" % (n, t, E, grad))
# 更新前の状態を描画
tangent = grad * (t_line - t) + E
img = plt.plot(t_line, tangent, color='r')
img.append(plt.scatter(t, E, color='r'))
img.append(plt.text(-8, 180, 'iteration: '+str(n), size='x-large'))
images.append(img)
# 更新
t = t - lr * grad
plt.xlim([-10, 20])
plt.ylim([-5, 100])
plt.xlabel('parameter t')
plt.ylabel('loss function E')
# アニメーション作成
anim = animation.ArtistAnimation(fig, images, interval=100)
# Google Colaboratoryの場合必要
rc('animation', html='jshtml')
plt.close()
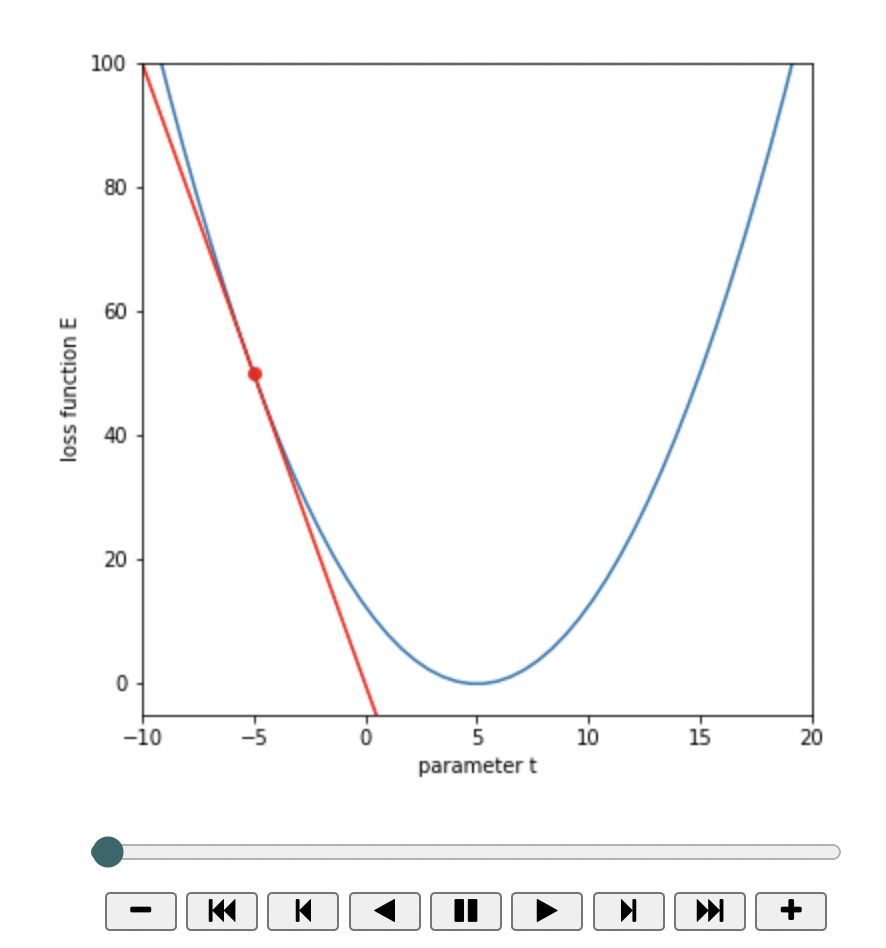
display(anim)傾きが小さくなるにつれて損失が小さくなっていくのが分かります。
0-th iteration, t=-5.000, loss: 50.000, grad: -10.000
1-th iteration, t=-4.000, loss: 40.500, grad: -9.000
2-th iteration, t=-3.100, loss: 32.805, grad: -8.100
3-th iteration, t=-2.290, loss: 26.572, grad: -7.290
4-th iteration, t=-1.561, loss: 21.523, grad: -6.561
5-th iteration, t=-0.905, loss: 17.434, grad: -5.905
6-th iteration, t=-0.314, loss: 14.121, grad: -5.314
7-th iteration, t=0.217, loss: 11.438, grad: -4.783
8-th iteration, t=0.695, loss: 9.265, grad: -4.305
9-th iteration, t=1.126, loss: 7.505, grad: -3.874
10-th iteration, t=1.513, loss: 6.079, grad: -3.487
40-th iteration, t=4.852, loss: 0.011, grad: -0.148
41-th iteration, t=4.867, loss: 0.009, grad: -0.133
42-th iteration, t=4.880, loss: 0.007, grad: -0.120
43-th iteration, t=4.892, loss: 0.006, grad: -0.108
44-th iteration, t=4.903, loss: 0.005, grad: -0.097
45-th iteration, t=4.913, loss: 0.004, grad: -0.087
46-th iteration, t=4.921, loss: 0.003, grad: -0.079
47-th iteration, t=4.929, loss: 0.002, grad: -0.071
48-th iteration, t=4.936, loss: 0.002, grad: -0.064
49-th iteration, t=4.943, loss: 0.002, grad: -0.057tが更新されていって、損失関数が最小に近づいていることがわかります。
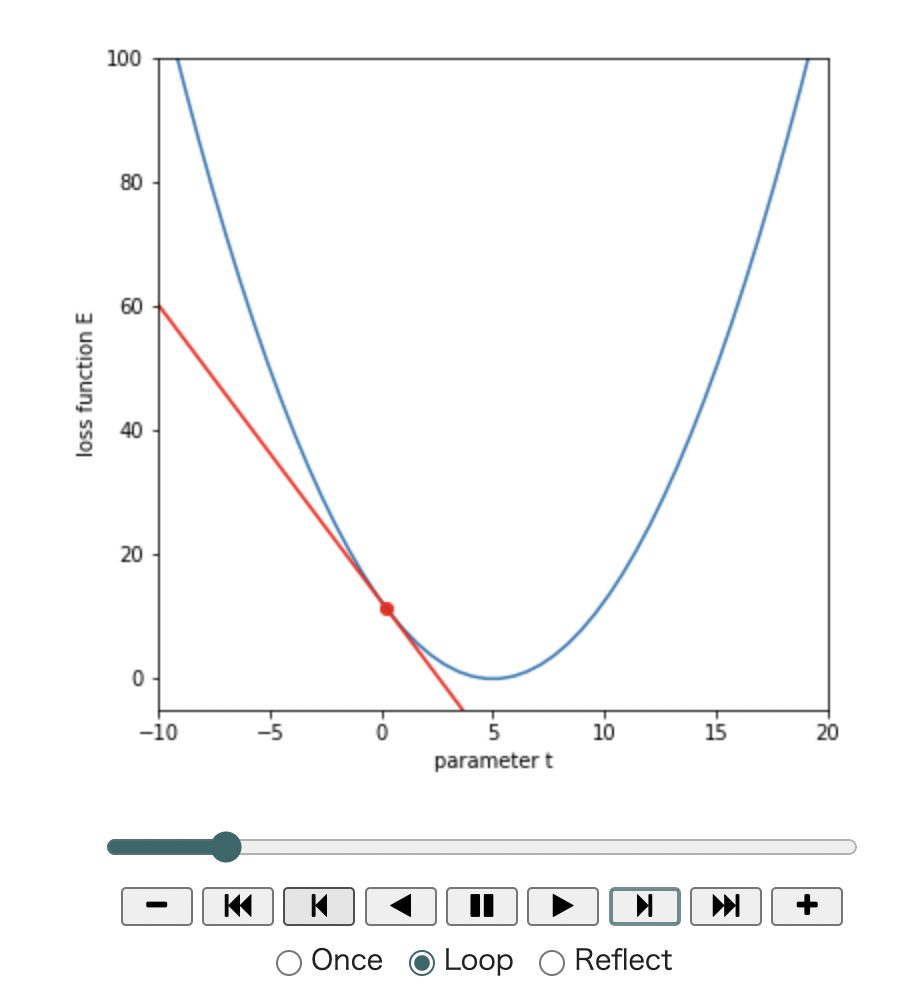
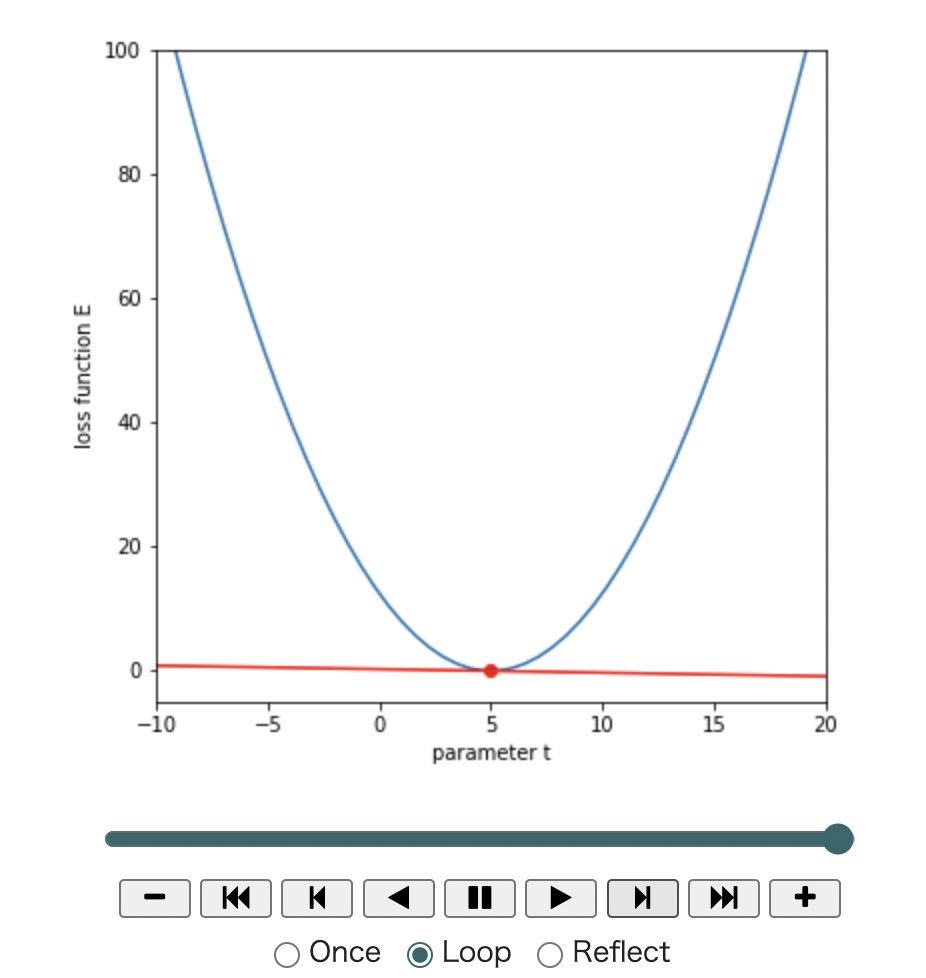
まとめ
勾配降下法とは、勾配を利用して、損失関数が最小になるパラメータを探索しようとしたもの
学習率はハイパーパラメータであり、適切な値に設定する必要がある
今回はニューラルネットワークの勾配降下法についてまとめました。
機械学習、ディープラーニングを学びたい方におすすめの入門書籍です。
ディープラーニングの理論が分かりやすくまとめられていて、力が身につくと思います。

最後まで読んでいただきありがとうございました。

他にもいろんな記事があるにゃ。


コメント