初めに
どーも、将棋と筋トレが好きな学生エンジニアのゆうき(@engieerblog_Yu)です。
今回はデータサイエンスに必要な統計編5回目にして、カイ二乗分布についてまとめていきたいと思います!
前回までの記事です。
カイ二乗分布とは?
カイ二乗分布の名前は、ギリシャ文字のχ(カイ)から来ていて、主に統計分析に用いられます。
例えば、仮説検定や信頼区間の計算などです。
カイ二乗分布を用いることで、分散が分からない分布から、分散の信頼区間を求めることができます。
カイ二乗分布は以下のようなグラフとなります。
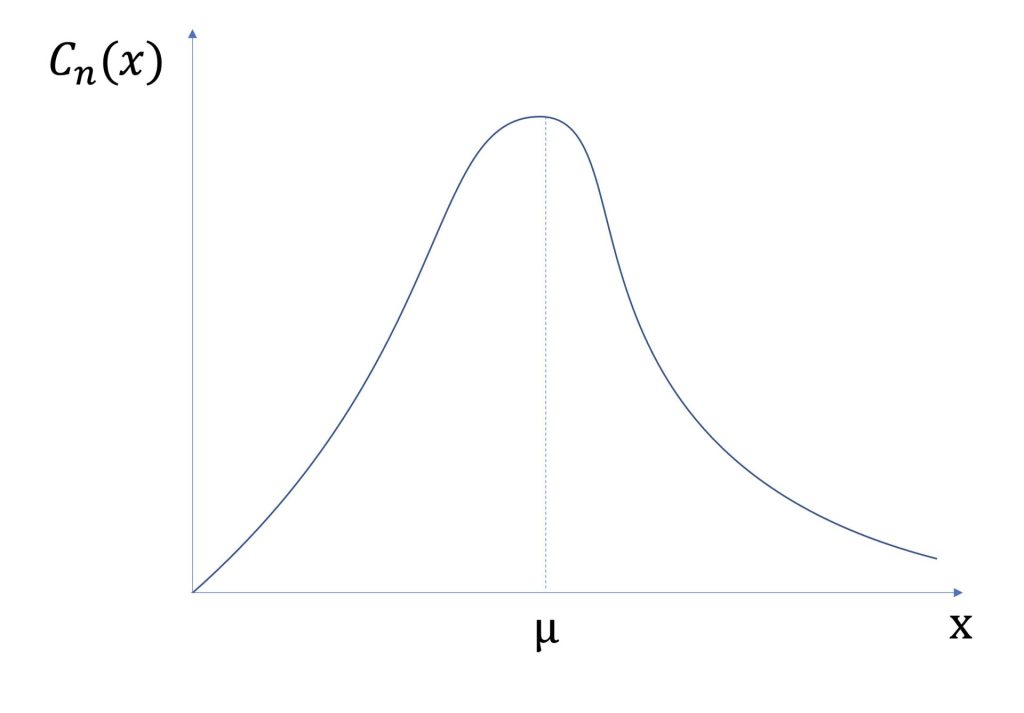
ガンマ関数の特徴は以下が挙げられます。
負の値を取らない
μと中心として左右非対称
自由度nによって分布の形が変わる
カイ二乗分布は以下で表されます。
互いに独立な確率変数\(Z_1,Z_2〜Z_n\)が標準正規分布に従うとき、\(X=Z_1^2+Z_2^2+〜Z_n^2\)は自由度nのカイ二乗分布に従う。
確率密度は以下によって表される。
\(C_n(x)=\frac{1}{2^{\frac{n}{2}}Γ(\frac{n}{2})}x^{\frac{n}{2}-1}e^{-\frac{x}{2}}\)
(自由度:n,Γ:ガンマ関数)
なにやらわけの分からない式が出てきたことと思います。
カイ二乗分布を理解するために、まずは式の中で使われているΓ(ガンマ)関数についてまとめていきます。
ガンマ関数について
ガンマ関数は以下のような式で表されます。
\(Γ(p)=\int_0^∞x^{p-1}e^{-x}dx\)
積分することでxが消えるので、pに従う式になります。
グラフで表すと以下のようになります。
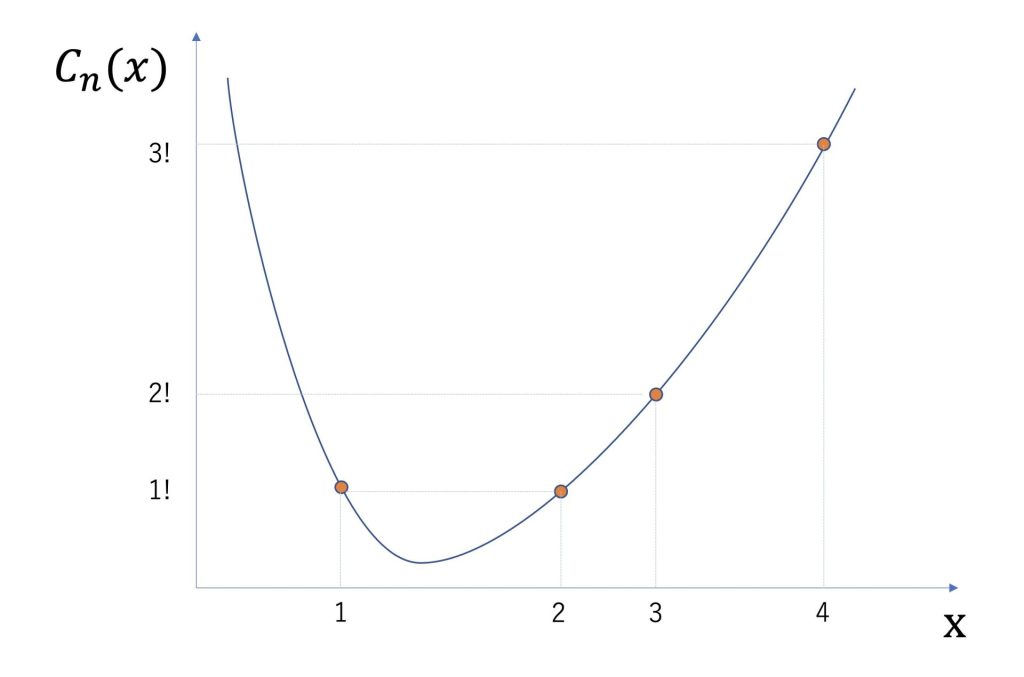
ガンマ関数の性質で重要なものは以下です。
\(Γ(p+1)=pΓ(p)\)
\(Γ(1)=1\)
\(Γ(\frac{1}{2})=\sqrt{π}\)
上記の性質から、nが自然数のときは、以下で簡単に表すことができます。
\(Γ(n)=(n-1)!\)
またnが\(\frac{1}{2},\frac{3}{2},\frac{5}{2}・・\)などの二分の一に1を足していくような数である場合も簡単に表すことができます。
\(n-1)(n-2)・・・\frac{3}{2}\frac{1}{2}\sqrt{π}\)
カイ二乗分布を導出する
カイ二乗分布が本当に以下の式で表されるのか、\(C_1(x)\)の値を試しに計算していきたいと思います。
\(C_n(x)=\frac{1}{2^{\frac{n}{2}}Γ(\frac{n}{2})}x^{\frac{n}{2}-1}e^{-\frac{x}{2}}\)
まずZ1は標準正規分布に従うので
\(f(Z_1)=\frac{1}{\sqrt{2π}}e^{-\frac{Z_1^2}{2}}\)
となります。
\(x=z_1^2\)より
\(z_1=\sqrt{x}\)
\(dz_1=\frac{1}{2\sqrt{x}}dx-①\)となります。
ここでxが負の時、カイ二乗分布は0になることに気をつけて、
\(\int_0^∞c_1(x)dx=1-②\)となります。
次に\(f(z_1)\)は偶関数ですので、
\(\int_∞^∞f(z_1)dz_1=2\int_0^∞f(z_1)dz_1=1\)となります。
①より
\(2\int_0^∞f(z_1)dz_1=\int_0^∞f(\sqrt{x})\frac{1}{\sqrt{x}}dx\)
となるので、②を用いて
\(c_1(x)=\frac{1}{\sqrt{x}}f(\sqrt{x})\)
\(=\frac{1}{\sqrt{x}}\frac{1}{\sqrt{2π}}e^{-\frac{x}{2}}\)
\(=\frac{1}{\sqrt{2π}}x^{-\frac{1}{2}}e^{-\frac{x}{2}}\)
よって自由度が1のカイ二乗分布を導出することができました。
一般には、数学的帰納法によって自由度がnのカイ二乗分布の公式を導出することができます。
まとめ
互いに独立な確率変数\(Z_1,Z_2〜Z_n\)が標準正規分布に従うとき、\(X=Z_1^2+Z_2^2+〜Z_n^2\)は自由度nのカイ二乗分布に従う。
確率密度は以下によって表される。
\(C_n(x)=\frac{1}{2^{\frac{n}{2}}Γ(\frac{n}{2})}x^{\frac{n}{2}-1}e^{-\frac{x}{2}}\)
今回はデータサイエンスに用いる統計5回目にして、カイ二乗分布についてまとめました!
次回はカイ二乗分布から求めることができる、t分布についてまとめていきたいと思います!

最後まで読んでいただきありがとうございました。

他にもいろんな記事があるにゃ。




コメント