目次
初めに
こんにちは。将棋と筋トレが好きな、学生エンジニアのゆうき(@engieerblog_Yu)です。
今回はニューラルネットワークの誤差逆伝播法についてまとめていきたいと思います。
誤差逆伝播法について

前回までの記事で勾配降下法を紹介しました。
勾配降下法は損失関数の値が小さくなる方向の勾配に、解を降下させていくといったものでした。
勾配を計算する方法は二つあり、数値微分と誤差逆伝播法です。
数値微分を用いると正確である反面、パラメータが大量になった場合、計算に時間がかかってしまうというデメリットがあります。
そこで使われるのが誤差逆伝播法で、実装が複雑という欠点はありますが、計算が早いので数値微分の代わりに用いられることがほとんどです。
誤差逆伝播法で実装し、数値微分で実装があっているか確認するという流れがどうやら主流であるようです。
勾配降下法で用いられる勾配を計算する方法は数値微分と誤差逆伝播法の二つ
数値微分は正確である反面、計算に時間がかかる
勾配降下法は実装が複雑という反面、計算が早い
誤差逆伝播法で勾配を計算し、数値微分で確認するのが主流
次に、誤差逆伝播法を理解するための計算グラフについてです。
計算グラフについて
ニューラルネットワークは以下のような計算グラフだと考えることができます。
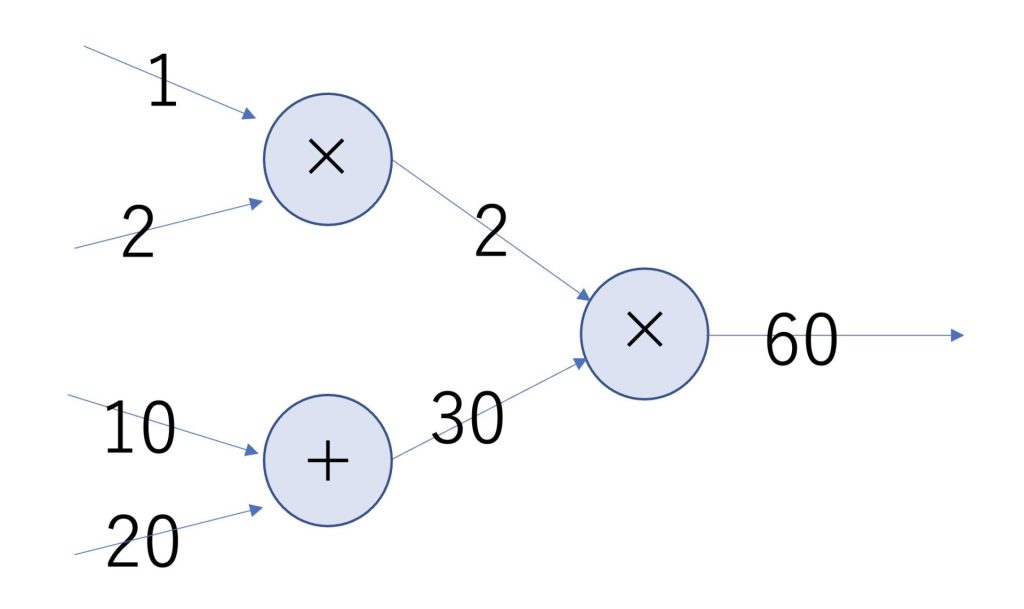
実際にニューラルネットワークを計算するほとんどの場合、行列を用いますが、今回は簡単のためにスカラー値で記述しました。
後ほど上記の計算グラフをPythonで実装します。
値が矢印で流れていき、ノードの記号により計算されます。
矢印が入力から出力であるものを順伝搬、出力から入力であるものを逆伝搬といいます。
計算グラフにおける逆伝搬について
xとyが入力として与えられて、最後の出力がLとなる場合を考えます。
すると逆伝搬は以下のように表されます。
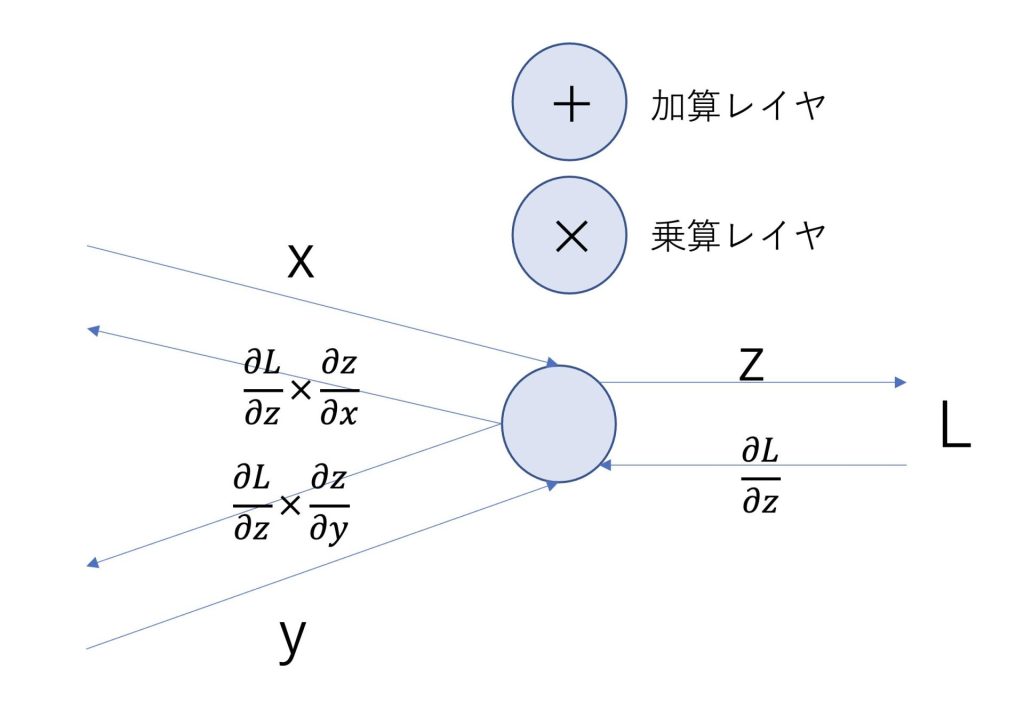
加算レイヤの場合は、x + y = z
乗算レイヤの場合は、x × y = z となります。
それでは実際に加算レイヤ・乗算レイヤをPythonで実装していきたいと思います。
加算レイヤをPythonで実装
加算レイヤの条件を以下のように設定します。
\(x+y=z\)
\(z=L\)
すると偏微分は以下のようになります。
\(\frac{∂L}{∂z}=1\)
\(\frac{∂L}{∂z}×\frac{∂z}{∂x}=1\)
\(\frac{∂L}{∂z}×\frac{∂z}{∂y}=1\)
AddLayerクラスを宣言して、Pythonで実装した結果です。
(xとyの値は適当に設定しました)
class AddLayer:
def forward(self,x,y):
out = x + y
return out
def backward(self,dout):
dx = dout * 1
dy = dout * 1
return dx,dyx = 20
y = 10
a = AddLayer()
out = a.forward(x,y)
print(out)
L = 1
print(a.backward(L))30
(1, 1)乗算レイヤをPythonで実装
乗算レイヤを以下のように設定します。
\(x×y=z\)
\(z=L\)
すると偏微分は以下のようになります。
\(\frac{∂L}{∂z}=1\)
\(\frac{∂L}{∂z}×\frac{∂z}{∂x}=y\)
\(\frac{∂L}{∂z}×\frac{∂z}{∂y}=x\)
MulLayerクラスを宣言して、Pythonで実装した結果です。
(xとyの値は適当に設定しました)
class MulLayer:
def __init__(self):
self.x = None
self.y = None
def forward(self,x,y):
self.x = x
self.y = y
out = x*y
return out
def backward(self,dout):
dx = dout * self.y
dy = dout * self.x
return dx,dyx = 10
y = 20
b = MulLayer()
out = b.forward(x,y)
print(out)
L = 1
print(b.backward(L))200
(22.0, 11.0)計算グラフをPythonで実装
それでは前述の計算グラフを順伝搬、逆伝搬に分けてPythonで実装していきます。
順伝搬は以下のように設定します。

まずは今回はレイヤーを三つ使うので、三つ宣言します。
mul_layer1 = MulLayer()
mul_layer2 = MulLayer()
add_layer1 = AddLayer()順方向の伝搬は以下で実装することができます。
out1 = mul_layer1.forward(1,2)
out2 = add_layer1.forward(10,20)
L = mul_layer2.forward(out1,out2)
print(L)60逆方向の伝搬は、偏微分を計算することで以下のようになります。
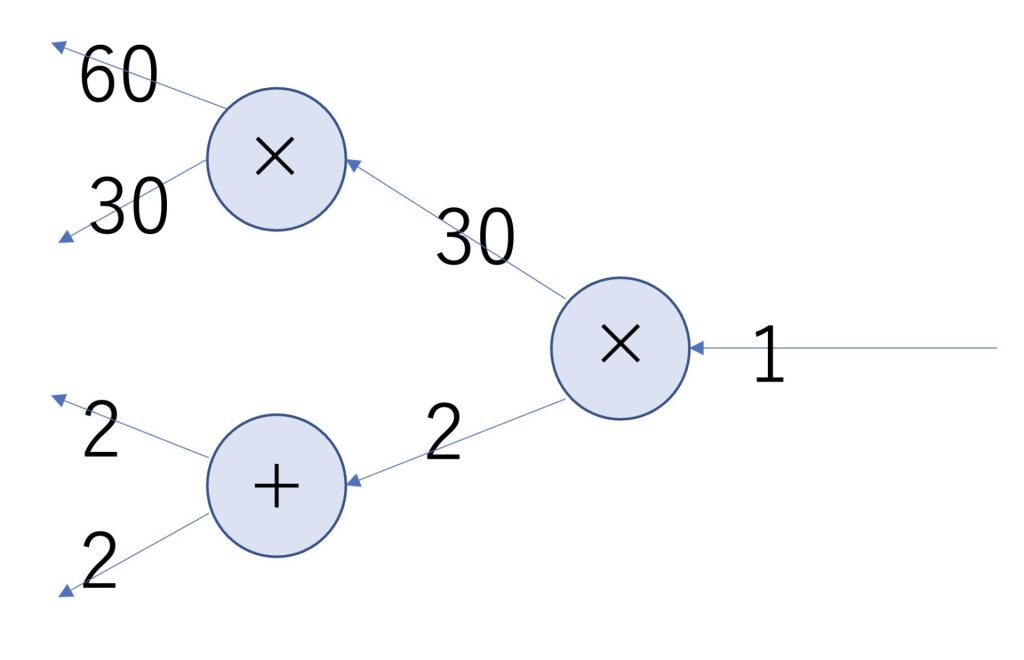
逆方向の伝搬は以下で実装することができます。
dout1,dout2 = mul_layer2.backward(1)
dout3,dout4 = mul_layer1.backward(dout1)
dout5,dout6 = add_layer1.backward(dout2)
print(dout3)
print(dout4)
print(dout5)
print(dout6)入力と一致していることが確認できます。
60
30
2
2まとめ
勾配降下法の勾配を実装するために、計算が早い誤差逆伝播法が使われている
誤差逆伝播法で勾配を計算し、計算が遅いが正確な数値微分によって確かめるのが一般的
逆伝搬は偏微分によって計算される
今回はニューラルネットワークの計算グラフの順伝搬・逆伝搬についてまとめました。
機械学習、ディープラーニングを学びたい方におすすめの入門書籍です。
ディープラーニングの理論が分かりやすくまとめられていて、コーディングしながら力を身につけたい方におすすめです。

最後まで読んでいただきありがとうございました。

他にもいろんな投稿があるにゃ。




コメント