目次
初めに
どーも、将棋と筋トレが好きな学生エンジニアのゆうき(@engieerblog_Yu)です。
今回は、PyTorchを使って、CIFAR-10の画像分類をやっていこうと思います。
今回は、Google ColaboratoryでGPUを使って実行しています。
CIFAR-10とは?
CIFAR-10とは、動物や乗り物のカラー画像が6万枚含まれているデータセットで、以下の種類の画像が含まれています。
- ラベル「0」: airplane(飛行機)
- ラベル「1」: automobile(自動車)
- ラベル「2」: bird(鳥)
- ラベル「3」: cat(猫)
- ラベル「4」: deer(鹿)
- ラベル「5」: dog(犬)
- ラベル「6」: frog(カエル)
- ラベル「7」: horse(馬)
- ラベル「8」: ship(船)
- ラベル「9」: truck(トラック)
今回はCIFAR-10を入力として、正解ラベルを出力するような画像分類モデルを、ニューラルネットワークで作っていきたいと思います。
ライブラリのインポート
今回はPyTorchを使って、ニューラルネットワークを作っていきます。
import torch
import torchvision
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
import torchvision.transforms as transforms
import numpy as np
from matplotlib import pyplot as plt
%matplotlib inlineデータセットのダウンロード
CIFAR-10はtorchvisionからダウンロードすることができるので、訓練データとテストデータに分けてダウンロードしていきます。
train_dataset = torchvision.datasets.CIFAR10(root='./data/',train=True,transform=transforms.ToTensor(),download=True)
test_dataset = torchvision.datasets.CIFAR10(root='./data/',train=False,transform=transforms.ToTensor(),download=True)
train_loader = torch.utils.data.DataLoader(dataset=train_dataset,batch_size=64,shuffle=True,num_workers=2)
test_loader = torch.utils.data.DataLoader(dataset=test_dataset,batch_size=64,shuffle=False,num_workers=2)ニューラルネットワークを定義する
CIFAR-10で与えられる画像は、サイズが32×32です。
それに加えてRGBが与えられるので、3×32×32となって三次元の入力データとなります。
今回は、三層のニューラルネットワークを定義していきたいと思います。
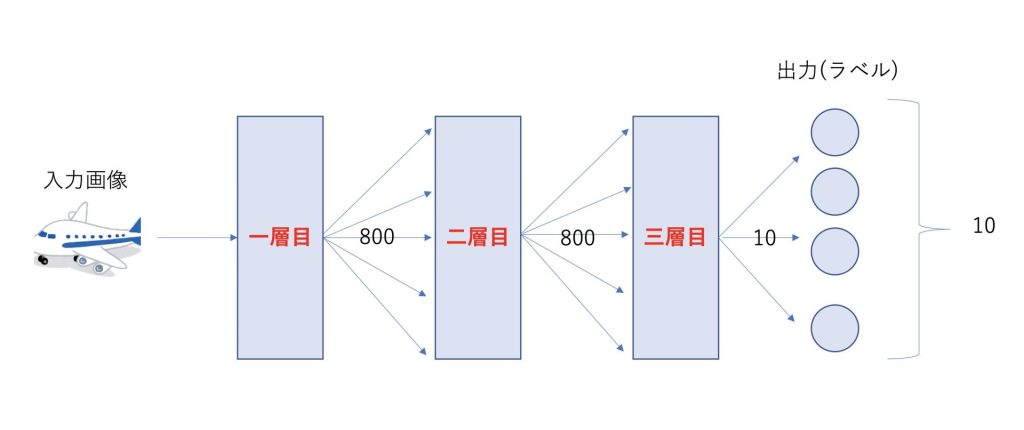
各々の層には線形レイヤとReLUレイヤ、ドロップアウトレイヤを含んでいます。
それぞれについて、具体的に何か知りたい方は以下の記事も併せてどうぞ。
上記の図に基づいて実装したものが以下になります。
# 分類数10
num_classes = 10
class MLPNet(nn.Module):
def __init__(self):
super(MLPNet,self).__init__()
# 画像を一次元に変換
self.fc1 = nn.Linear(32*32*3,800)
self.fc2 = nn.Linear(800,800)
self.fc3 = nn.Linear(800,num_classes)
self.dropout1 = nn.Dropout2d(0.2)
self.dropout2 = nn.Dropout2d(0.2)
def forward(self,x):
x = F.relu(self.fc1(x))
x = self.dropout1(x)
x= F.relu(self.fc2(x))
x = self.dropout2(x)
x = F.relu(self.fc3(x))
return x
#GPUの利用
device = 'cuda' if torch.cuda.is_available() else 'cpu'
net = MLPNet().to(device)次にニューラルネットワークの学習に用いる損失関数と最適化関数を定義していきます。
損失関数と最適化関数を定義
今回は分類問題ですので、交差エントロピー誤差を使っていきます。
#交差エントロピー誤差を使用
criterion = nn.CrossEntropyLoss()
#モーメンタム法を使用
optimizer = optim.SGD(net.parameters(),lr=0.01,momentum=0.9,weight_decay=5e-4)最適化関数をモーメンタム法の代わりに、Adamなどを用いてみてもいいかもしれません。
モデルの学習と評価
それではモデルの学習と評価をしていきます。
実行には10分程度かかるかもしれません。
# 繰り返し回数
num_epochs = 70
train_loss_list = []
train_acc_list = []
val_loss_list = []
val_acc_list = []
for epoch in range(num_epochs):
# 値の初期化
train_loss = 0
train_acc = 0
val_loss = 0
val_acc = 0
# ここから訓練
net.train()
for i,(images,labels) in enumerate(train_loader):
images,labels = images.view(-1,32*32*3).to(device),labels.to(device)
# 勾配を0にする
optimizer.zero_grad()
# 順伝播の計算
outputs = net(images)
# 誤差の計算
loss = criterion(outputs,labels)
# 訓練誤差
train_loss += loss.item()
# 予測結果と正解ラベルが同じ数(同じ場合に1となる)
train_acc += (outputs.max(1)[1]==labels).sum().item()
# 誤差の逆伝播
loss.backward()
# 重みの更新
optimizer.step()
# 訓練誤差の平均
avg_train_loss = train_loss / len(train_loader.dataset)
# 正解率(訓練)の平均
avg_train_acc = train_acc / len(train_loader.dataset)
# ここから評価(dropoutやバッチ正規化を定義した場合に必要)
net.eval()
# 学習モデルを固定
with torch.no_grad():
for i,(images,labels) in enumerate(test_loader):
images,labels = images.view(-1,32*32*3).to(device),labels.to(device)
# 順伝播の計算
outputs = net(images)
# 誤差の計算
loss = criterion(outputs,labels)
# 評価誤差
val_loss += loss.item()
# 正解率(評価)
val_acc += (outputs.max(1)[1]==labels).sum().item()
# 評価誤差の平均
avg_val_loss = val_loss / len(test_loader.dataset)
# 正解率(評価)の平均
avg_val_acc = val_acc / len(test_loader.dataset)
# プロット用リストへの格納
train_loss_list.append(avg_train_loss)
train_acc_list.append(avg_train_acc)
val_loss_list.append(avg_val_loss)
val_acc_list.append(avg_val_acc)結果のプロット
それでは結果をプロットしていきます!
plt.figure()
plt.plot(range(num_epochs),train_loss_list,label='train_loss')
plt.plot(range(num_epochs),val_loss_list,label='val_loss')
plt.legend()
plt.xlabel('epoch')
plt.ylabel('loss')
plt.title('Training and Validation loss')
plt.grid()結果を見てみると繰り返し回数に応じて、訓練誤差は小さくなっているのに対し、評価誤差は途中からあまり変わらなくなっていることがわかります。
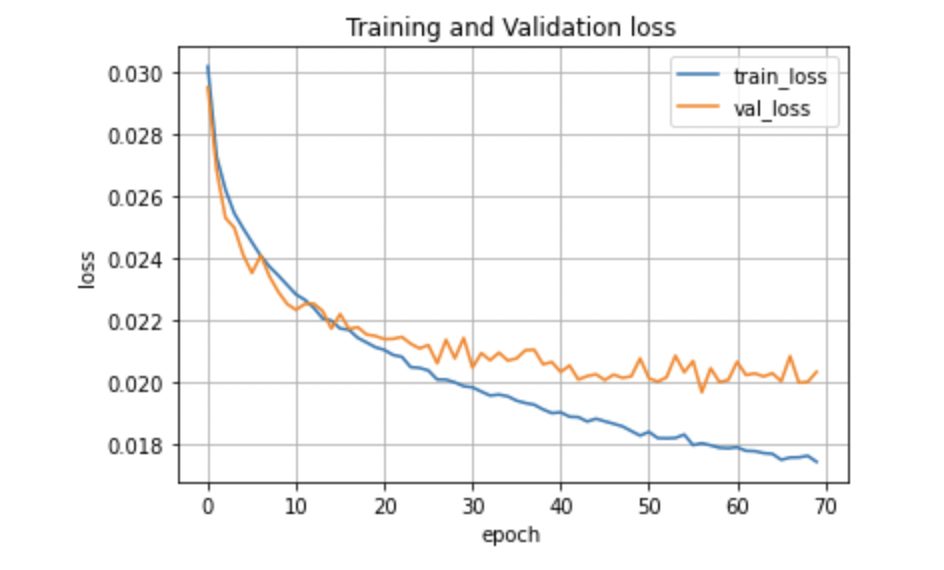
今回のニューラルネットワークでは、誤差を0.020程度に抑えるのが限界のようですね。
興味がある方は、Adamなどを使って試してみるとより良い結果になるかもしれません。
plt.figure()
plt.plot(range(num_epochs),train_acc_list,label='train_acc')
plt.plot(range(num_epochs),val_acc_list,label='val_acc')
plt.legend()
plt.xlabel('epoch')
plt.ylabel('acc')
plt.title('Training and Validation accuracy')
plt.grid()正解率をプロットしてみると、訓練データでの正解率は60%程度であるのに対し、評価データでは55%程度でした。
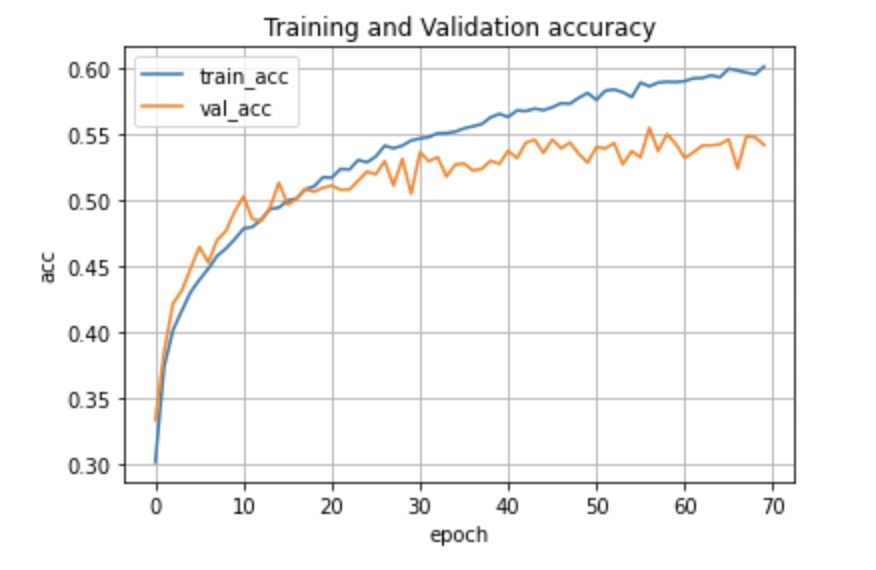
やはり画像分類では、畳み込みニューラルネットワークを使った方が精度が良くなるので、ニューラルネットワークの限界はこの程度なのかもしれません。
次回の記事で、畳み込みニューラルネットワークで画像分類を行っていきたいと思います!

最後まで読んでいただきありがとうございました。

他にもいろんな記事があるにゃ。







コメント