はじめに
こんにちは。将棋と筋トレが好きな、学生エンジニアのゆうき(@engieerblog_Yu)です。
今回はニューラルネットワークのモデルの学習に使われる損失関数についてまとめていきたいと思います。
前回の記事です。
ニューラルネットワークの学習について
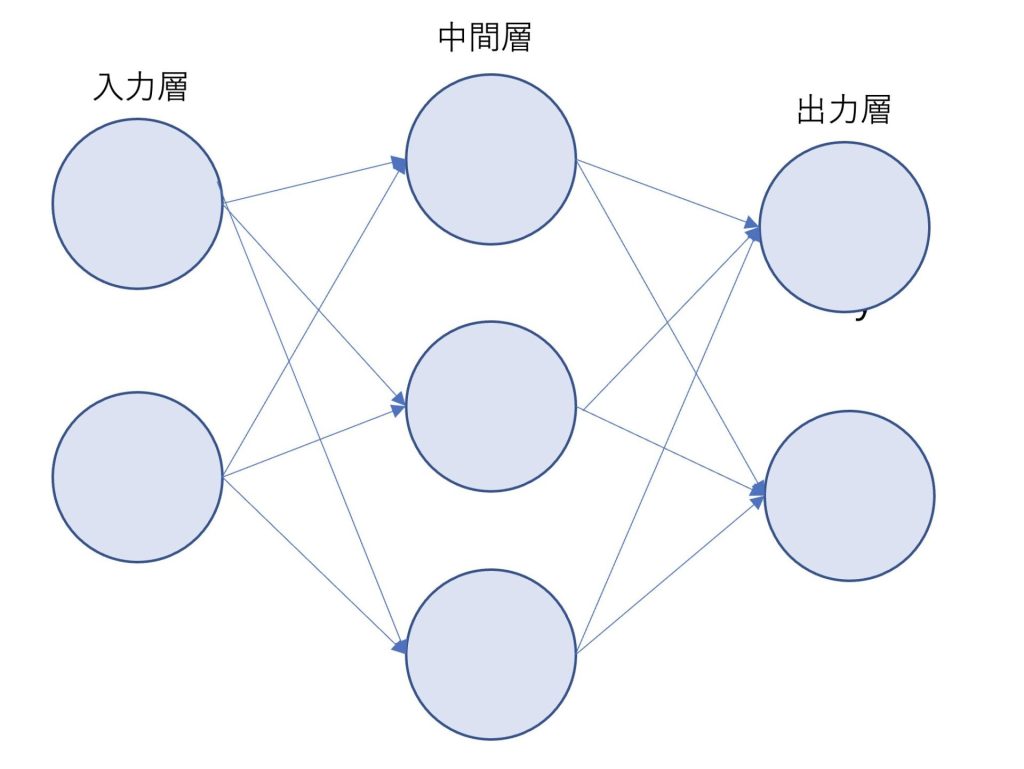
ニューラルネットワークと前回紹介したパーセプトロンでは、重みを自動で学習できるか、できないかといった違いがありました。
パーセプトロンは手作業で重みを決めなければならない
ニューラルネットワークは重みを自動で学習できる
どのように学習していくのかというと、数値微分を行い、重みの値を適切な値に少しずつ近づけていきます。
そのような方法を勾配降下法といいます。
勾配降下法については、また別の記事でまとめていきたいと思います。
今回まとめる損失関数は、勾配降下法で重みパラメータを更新するために使われます。
損失関数は、勾配降下法で重みパラメータを更新するときに使われるもの
イメージとしては誤差が小さくなるように重みを調整していくといった感じです。
二乗和誤差
モデルの学習を行う際の正解データをy、予想データをtとします。
二乗和誤差はその名の通り、データの誤差の二乗和をとったものです。
\(E=\frac{1}{2}\sum_{k}(y_k-t_k)^2\)
yとt以下のように設定して、二乗和誤差を求めます。
y = [0,0,1,0]
t = [0.05,0.2,0.7,0.05]def sum_squared_error(y,t):
return (np.sum(y-t)**2)/2print(sum_squared_error(np.array(y),np.array(t)))二乗和誤差は以下のようになりました。
0.06750000000000002当たり前ですが、誤差は必ず正の値を取ります。
交差エントロピー誤差
\(E=-\sum_{k}t_klogy_k\)
マイナス無限大の値が発生してしまうと、プログラミングできなくなってしまうので、deltaを導入しています。
def cross_entropy(y,t):
delta = 1e-10
return -np.sum(t * np.log(y + delta))print(cross_entropy(np.array(y),np.array(t)))6.907755278912138交差エントロピー誤差は二乗和誤差と比べて、正解yと予測tの値が離れるほど、誤差の値が大きくなる傾向があります。
訓練データとテストデータについて

機械学習では、訓練データとテストデータに分けて学習と検証を行うのが主流となっています。
データが100あったとしたら70のデータを訓練データとし、30のデータをテストデータとするようなことです。
訓練データを使ってニューラルネットワークの学習を行い、テストデータを使ってモデルの精度がどのくらいなのか検証します。
機械学習ではデータを二つに分ける必要がある
訓練データを使ってモデルの学習を行い、テストデータを使ってモデルの精度を検証する
まとめ
パーセプトロンは手作業で重みを決めなければならない
ニューラルネットワークは重みを自動で学習できる
損失関数は、勾配降下法で重みパラメータを更新するときに使われるもの
機械学習ではデータを二つに分ける必要がある
訓練データを使ってモデルの学習を行い、テストデータを使ってモデルの精度を検証する
今回はニューラルネットワークの勾配降下法に用いられる損失関数についてまとめました。
機械学習、ディープラーニングを学びたい方におすすめの入門書籍です。
ディープラーニングの理論が分かりやすくまとめられていて、力が身につくと思います。

最後まで読んでいただきありがとうございました。

他にもいろんな記事があるにゃ。


コメント