目次
はじめに
こんにちは。将棋と筋トレが好きな、情報系大学生のゆうき(@engieerblog_Yu)です。
今回はニューラルネットワークの最適化問題を解く手法である、AdaGradについてまとめていきたいと思います。
AdaGradとは?
AdaGradとは、勾配降下法に学習率の減衰を取り入れたものです。
ニューラルネットワークの学習では学習率が大きすぎると、振動が起こったり、発散してしまいます。
反対に学習率が小さすぎると学習までに多くの時間がかかってしまいます。
そのどちらも防ぐために有効な手段が学習率の減衰です。

AdaGradは以下の式で表されます。
\(h_{next} = h_{initial} + \frac{∂L}{∂x}・\frac{∂L}{∂x}\)
\(x_{next} = x_{initial} – η\frac{1}{\sqrt{h}}\frac{∂L}{∂x}\)
前回の記事でも解説しましたが、勾配降下法は以下の式でパラメータの更新を行なっていきます。
\(x_{next} = x_{initial} – η\frac{∂L}{∂x}\)
式からも、AdaGradは勾配降下法に学習率の減衰を取り入れていることがわかります。
AdaGradは勾配降下法に学習率の減衰を取り入れたもの

それではAdaGradをPythonで実装していきたいと思います。
ライブラリのインポート
import numpy as np
import matplotlib.pyplot as plt
import mathAdaGradクラス
update関数でAdaGradの式を実装していきます。
\(h_{next} = h_{initial} + \frac{∂L}{∂x}・\frac{∂L}{∂x}\)
\(x_{next} = x_{initial} – η\frac{1}{\sqrt{h}}\frac{∂L}{∂x}\)
class AdaGrad:
def __init__(self,lr):
self.lr = lr
self.h = None
# パラメータの更新
def update(self,grad,x_initial):
if self.h is None:
self.h = 0
self.h = self.h + grad**2
x_next = x_initial - self.lr * grad / (math.sqrt(self.h)+1e-7)
return x_next損失関数の設定
今回の損失関数は以下のように設定します。
\(f(x)=5x^2+3x\)
\(\frac{df}{dx}=10x+3\)
# 損失関数の設定
def loss_function(x):
L = 5*x**2 + 3*x
return L# 勾配の計算
def calc_gradient(x):
grad = 10*x + 3
return grad初期状態
xの初期位置は-5とします。
# xの初期値
x_initial = -5
# 損失値
L = loss_function(x_initial)
# 損失関数をプロットする
x_line = np.linspace(-10, 20)
L_line = loss_function(x_line)
plt.figure(figsize=(6,6))
plt.plot(x_line, L_line)
plt.xlabel('parameter x')
plt.ylabel('loss function L')
# 現在の x と損失値をプロット
plt.scatter(x_initial, L, color='r')
plt.xlim([-10, 10])
plt.ylim([-5, 300])
plt.show()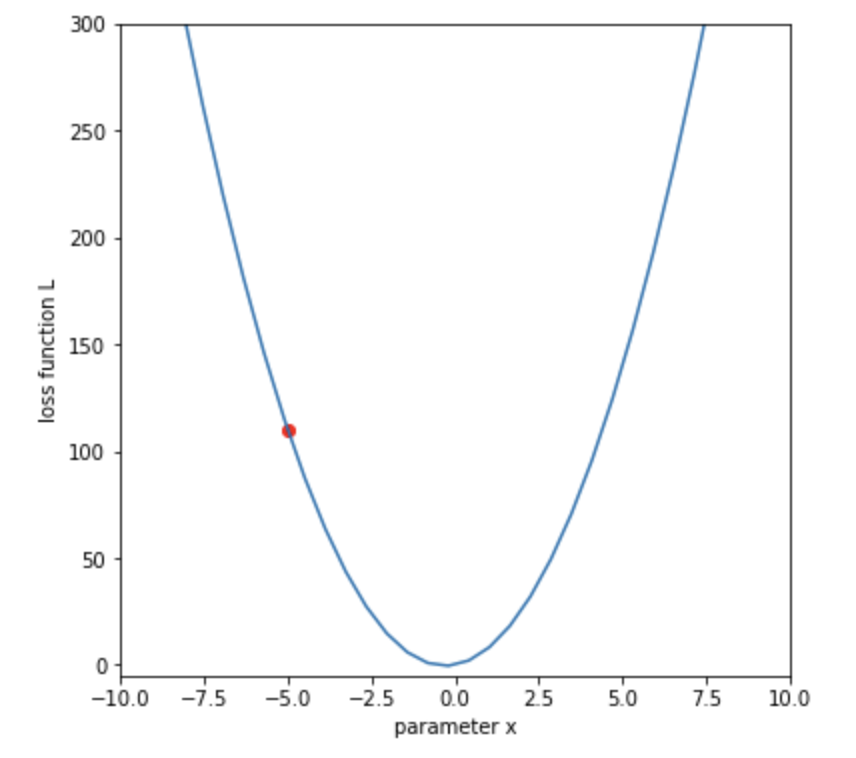
損失関数を最小とするのが目標です。
今回は-0.5くらいの値になりそうです。
AdaGradを使った損失関数の最小化
AdaGradの学習率は後に小さくなってしまうので最初は大きめにしておくことがポイントです。
from matplotlib import animation, rc
from IPython.display import HTML
# 学習率(lr = learning rate)
lr = 2
# AddGradオブジェクトの宣言
adagrad = AdaGrad(lr)
# 更新回数
num_iterations = 50
# 初期値をコピー
x = x_initial
# 描画
fig = plt.figure(figsize=(6,6))
plt.plot(x_line, L_line)
images = []
for n in range(num_iterations):
# 損失値を計算
L = loss_function(x)
# 勾配を計算
grad = calc_gradient(x)
print("%d-th iteration, x=%.3f, loss: %.3f, grad: %.3f" % (n, x, L, grad))
# 更新前の状態を描画
tangent = grad * (x_line - x) + L
img = plt.plot(x_line, tangent, color='r')
img.append(plt.scatter(x, L, color='r'))
img.append(plt.text(-8, 300, 'iteration: '+str(n), size='x-large'))
images.append(img)
# 更新
x = adagrad.update(grad,x)
plt.xlim([-10, 10])
plt.ylim([-5, 400])
plt.xlabel('parameter x')
plt.ylabel('loss function L')
# アニメーション作成
anim = animation.ArtistAnimation(fig, images, interval=100)
# Google Colaboratoryの場合必要
rc('animation', html='jshtml')
plt.close()
display(anim)最初はパラメータが大きく更新されて、徐々に更新の幅が小さくなっていくことがわかります。
損失関数が最小となっていることがわかります。
補足ですがAdaGradは学習率の減衰を取り入れることで最初は大きくパラメータを更新し、徐々に小さくすることができます。
しかしその反面、時間が経つと学習がほとんど全く進まなくなってしまうので、その点に気を付けることが大切です。
【補足】Adamについて
前回のMomentumとAdaGradを組み合わせたような手法としてAdamがあります。
Adamは最近使われることが多くなってきている手法で、学習率の減衰と物理的な法則を組み合わせた手法です。
以下参考文献です。
Adam: A Method for Stochastic Optimization
https://arxiv.org/abs/1412.6980
まとめ
AdaGradとは勾配降下法に学習率の減衰を取り入れたもの
AdaGradの学習率は、小さくなっていくので学習が進まなくなることもある
今回はニューラルネットワークのAdaGradについてまとめました。
機械学習、ディープラーニングを学びたい方におすすめの入門書籍です。
ディープラーニングの理論が分かりやすくまとめられていて、力を身につけたい方におすすめです。

最後まで読んでいただきありがとうございました。

他の記事もおすすめにゃ。


コメント