初めに
こんにちは。将棋と筋トレが好きな、情報系大学生のゆうき(@engieerblog_Yu)です。
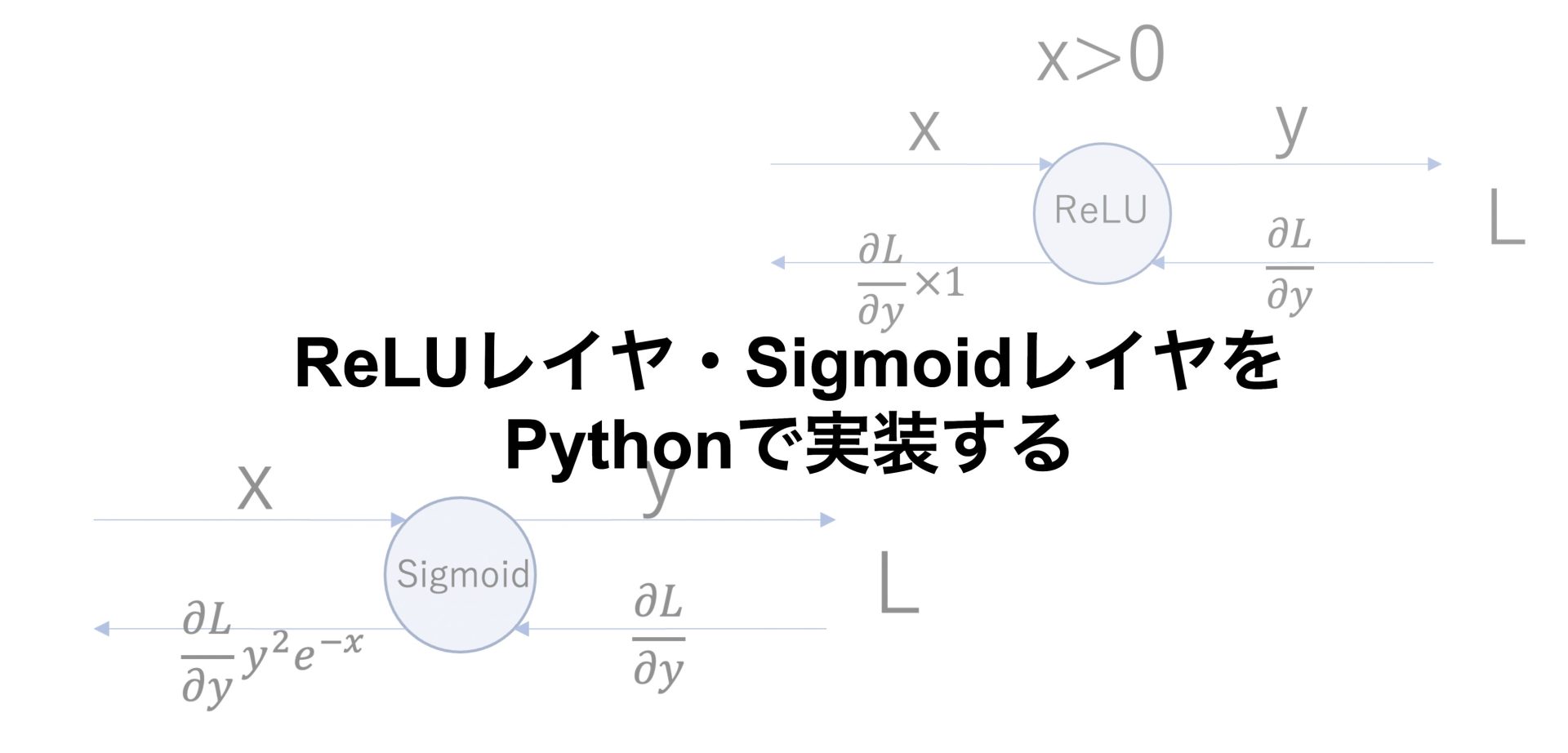
今回はニューラルネットワークの勾配の計算に用いられる誤差逆伝播法のReLUレイヤ・Sigmoidレイヤについてまとめていきたいと思います。
誤差逆伝播法について

前回までの記事で勾配降下法を紹介しました。
勾配降下法は損失関数の値が小さくなる方向の勾配に、解を降下させていくといったものでした。
勾配を計算する方法は二つあり、数値微分と誤差逆伝播法です。
数値微分を用いると正確である反面、パラメータが大量になった場合、計算に時間がかかってしまうというデメリットがあります。
そこで使われるのが誤差逆伝播法で、実装が複雑という欠点はありますが、計算が早いので数値微分の代わりに用いられることがほとんどです。
誤差逆伝播法で実装し、数値微分で実装があっているか確認するという流れがどうやら主流であるようです。
誤差逆伝播法で用いられる計算グラフや逆伝播の法則については、こちらの記事で解説しているので合わせてどうぞ。
ReLUレイヤ
ReLU関数、シグモイド関数については以下の記事でまとめてあります。
ReLUレイヤは以下の条件で表すことができます。
\( y= \begin{cases} x & \text{if $x>0$} \\ 0 & \text{if $x<=0$} \end{cases}\)
\( \frac{∂y}{∂x}= \begin{cases} 1 & \text{if $x>0$} \\ 0 & \text{if $x<=0$} \end{cases}\)
計算グラフで表すと以下のようになります。
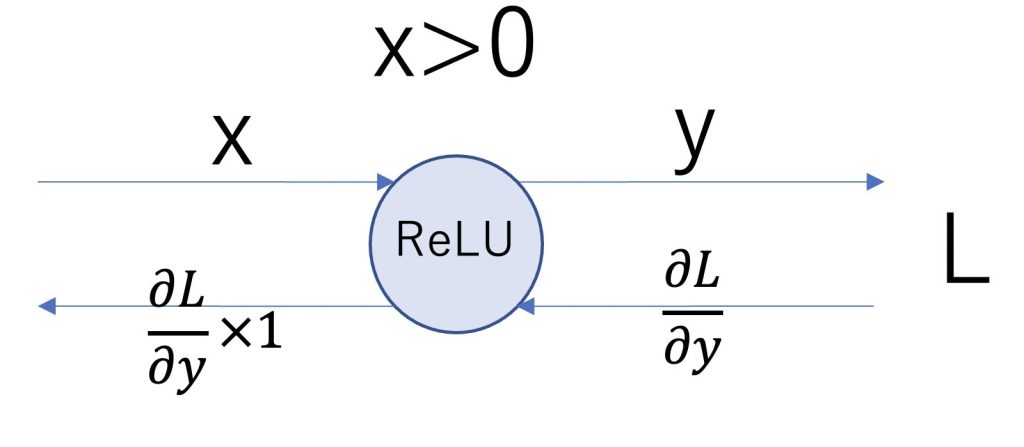
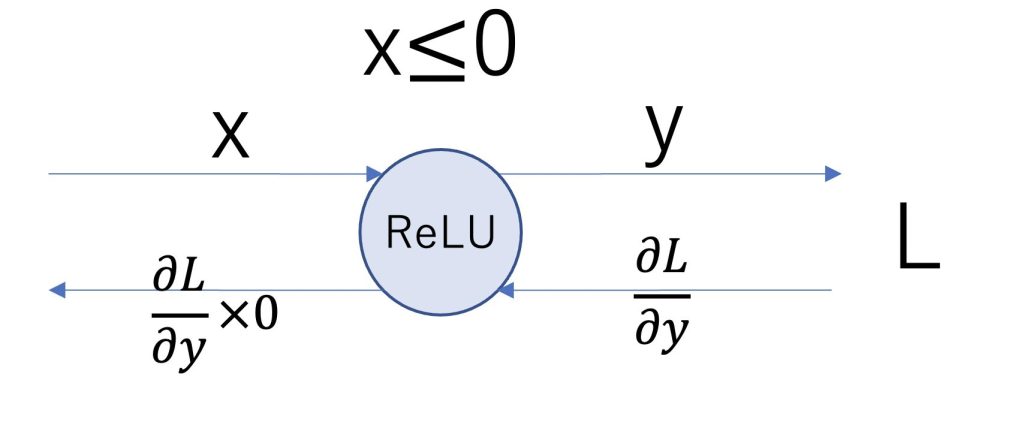
以下がPythonで実装した例です。
class Relu:
def __init__(self):
self.mask = None
def forward(self,x):
if x > 0:
self.mask == None
out = x
else:
self.mask = True
out = 0
return out
def backward(self,dout):
if self.mask == None:
dx = dout * 1
else:
dx = dout * 0
return dxmaskを設定して、逆伝搬を行うときに0になるかならないかを設定しました。
relu1 = Relu()
relu2 = Relu()
print(relu1.forward(10))
print(relu1.backward(1))
print(relu2.forward(-5))
print(relu2.backward(1))正の数をreluレイヤに通した場合はそのまま通り、負の数をreluに通したときは0になっていることが確認できます。
10
1
0
0Sigmoidレイヤ
Sigmoidレイヤは以下の条件で表されます。
\(y=\frac{1}{1+e^{-x}}\)
シグモイドレイヤは、指数関数や分数を含んだ式から構成されるので少し大変です。
結論から言うと以下のような計算グラフになります。
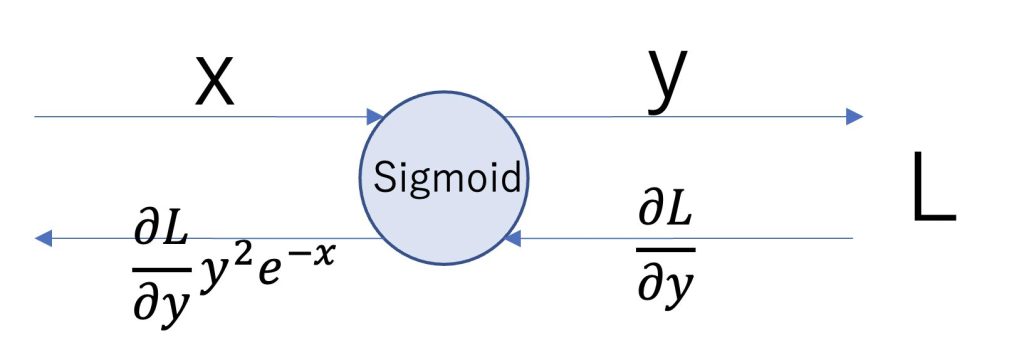
何故上記のようになったのか説明していきます。
Sigmoidレイヤを細かく分割してみると、以下のような計算グラフになります。
expは指数関数、/は分数を表しています。
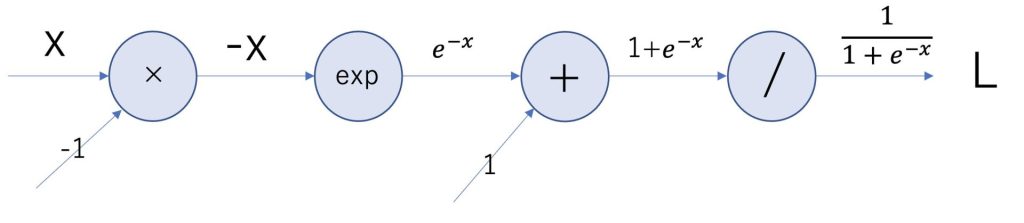
上記のような計算グラフの逆伝播を求めていきます。
分数と指数関数のレイヤは、以下の式で表されます。
\(/:y = \frac{1}{x} ,\frac{∂y}{∂x}=-y^2\)
\(exp:y=e^x,\frac{∂y}{∂x}=e^x\)
すると逆伝播は以下のように計算グラフにすることができます。
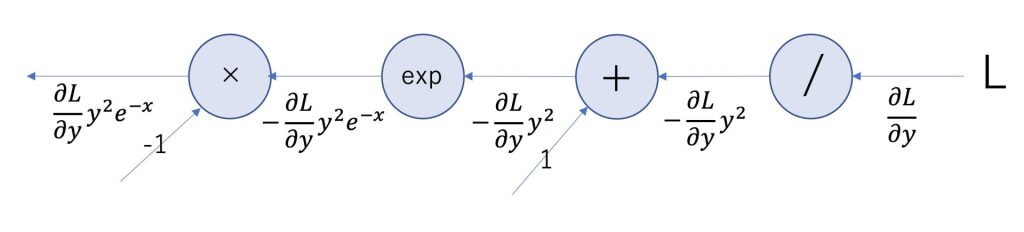
このようにして簡略化したSigmoidレイヤが正しいことがわかります。

それではSigmoidレイヤをPythonで実装してみます。
import numpy as np
class Sigmoid:
def __init__(self):
self.out = None
def forward(self,x):
out = 1 / (1 + np.exp(-x))
self.out = out
return out
def backward(self,dout):
dx = dout * (1.0 - self.out) * self.out
return dxsigmoid = Sigmoid()
print(sigmoid.forward(10))
print(sigmoid.backward(1))0.9999546021312976
4.5395807735907655e-05まとめ
今回はニューラルネットワークの勾配降下法に用いられる誤差逆伝播法のReLUレイヤ・Sigmoidレイヤについてまとめました。
機械学習、ディープラーニングを学びたい方におすすめの入門書籍です。
ディープラーニングの理論が分かりやすくまとめられていて、コーディングしながら力を身につけたい方におすすめです。

最後まで読んでいただきありがとうございました。

他にもいろんな投稿があるにゃ。





コメント