初めに
どーも、将棋と筋トレが好きな学生エンジニアのゆうき(@engieerblog_Yu)です。
今回はデータサイエンスに必要な統計編4回目にして、前回の正規分布の記事の続きとして標準正規分布についてまとめていきたいと思います!
前回の記事を読んでいない方は合わせてどうぞ。
分布の変換について
前回紹介した正規分布を標準正規分布にするためには、標準化という操作が必要です。
標準化について理解するためには、分布の変換について理解する必要があります。
例えば、平均μの正規分布が以下のようにあったとします。
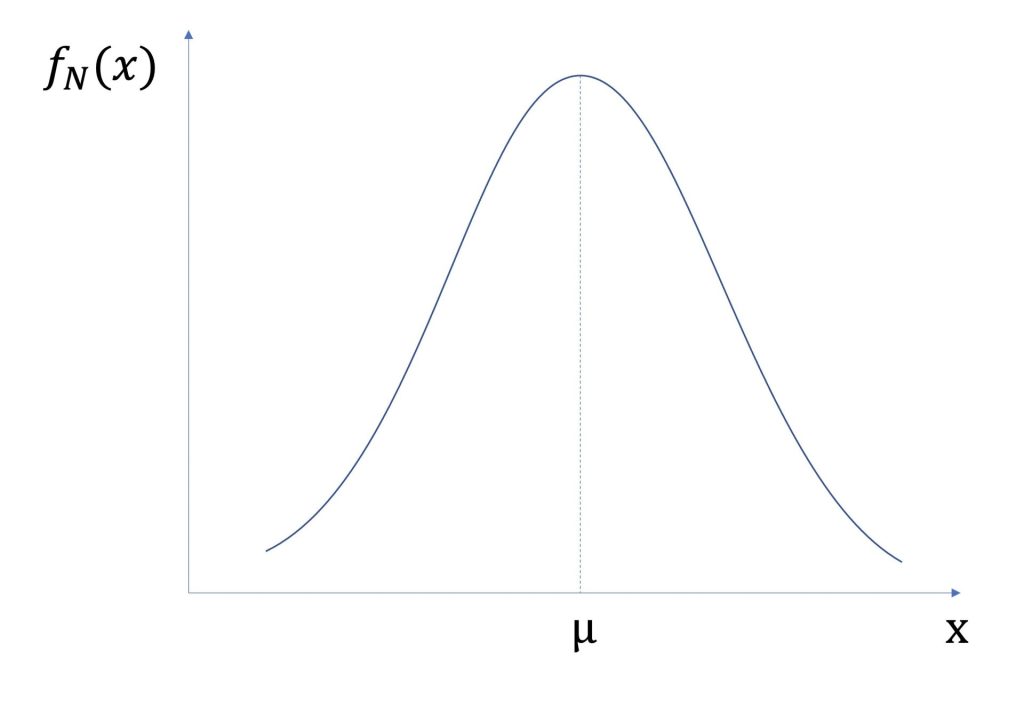
変換するためには、四則演算を行います。
具体的には以下のようになります。
足す→負の方向に平行移動
引く→正の方向に平行移動
掛ける→縮む(掛ける数が0から1の場合は伸びる)
割る→伸びる(割る数が0から1の場合は縮む)
一つずつ見ていきましょう。
以下は、先ほどの正規分布に+3した時の図です。
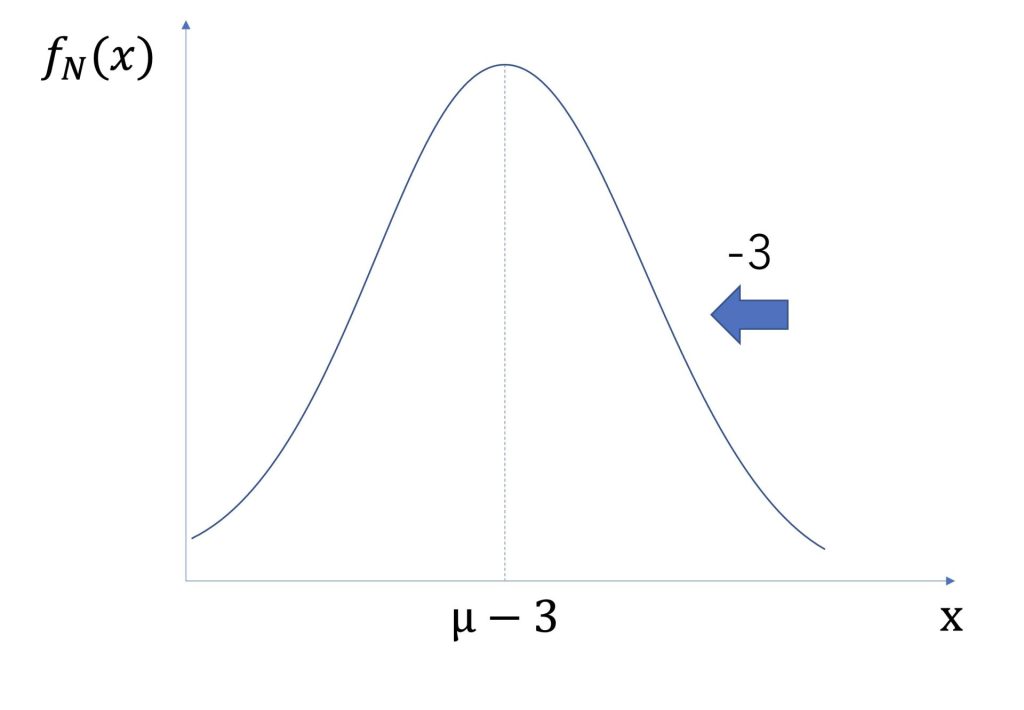
負の方向に-3平行移動していることが分かります。
−3した場合も同様です。
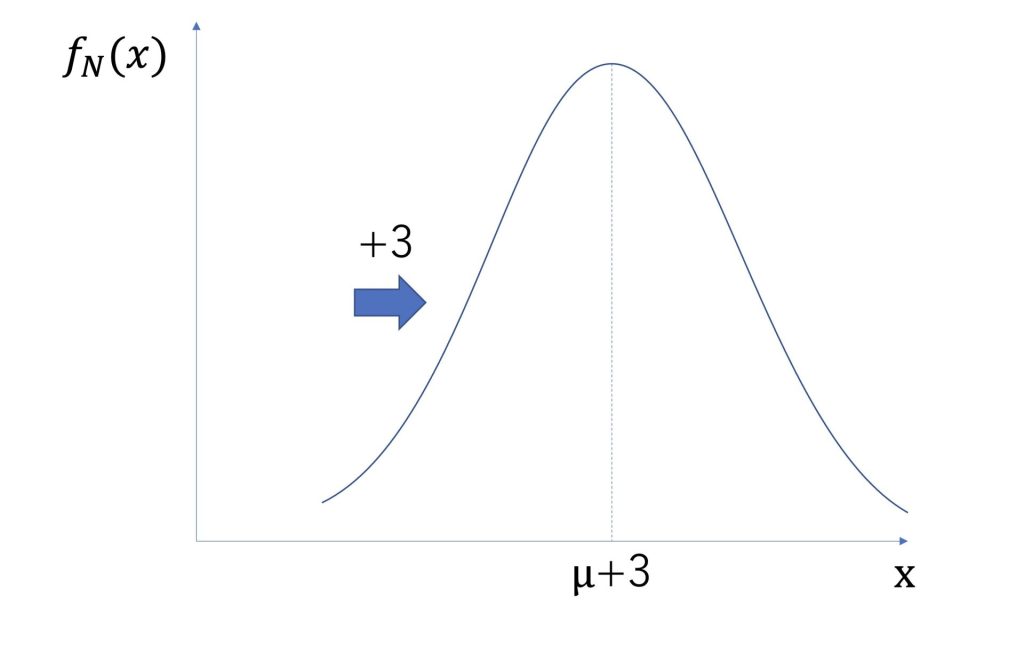
引いた場合は正の方向に+3平行移動します。
次に掛けた場合です。
掛けた場合は平均は変わらず、分散が変わります。
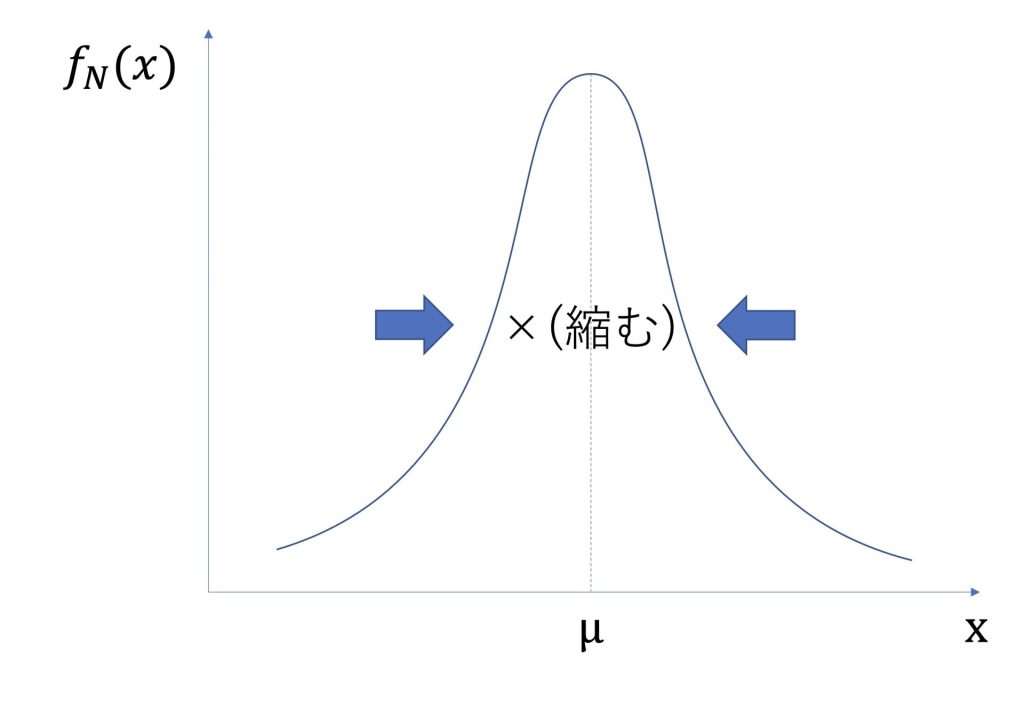
掛けた値が1以上であった場合、その倍率の分だけ分布は縮みます。
反対に掛けた値が0から1の場合は分布は伸びます。
最後に割った場合です。
掛けた場合とは反対に、割った値の分だけ、分布が伸びます。(値が1以上の場合)
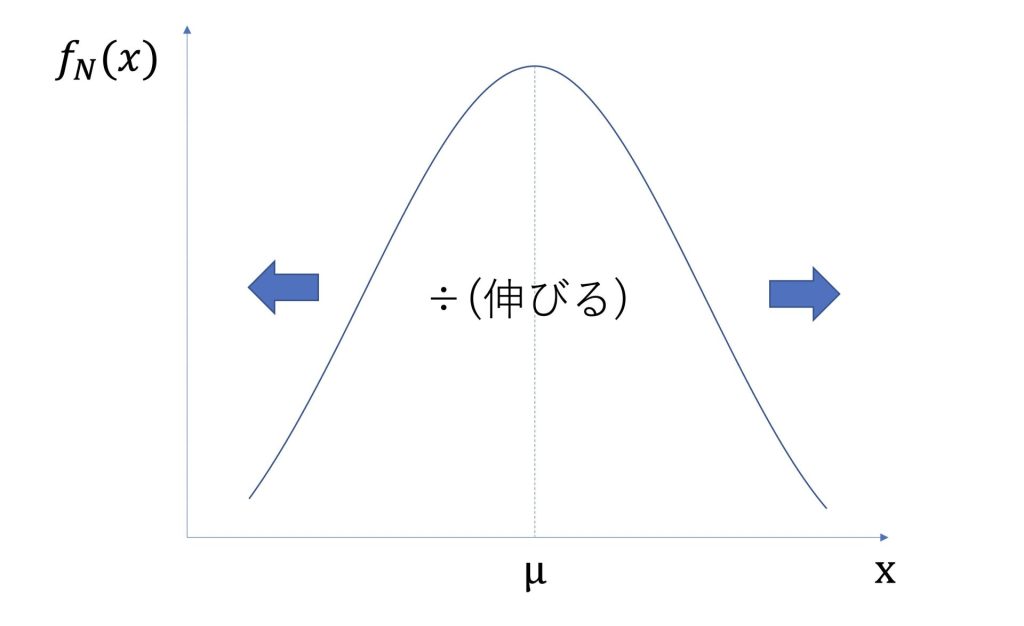
値が0から1の場合は、その分だけ分布が縮みます。
分布に四則演算を行うと分布の平均や分散の値を変えることができるということが分かりました。
それでは次に標準化についてです。
標準化について
標準化とは、分布の種類を変えずに平均0、分散1にする操作のことを言います。
つまり標準正規分布とは、正規分布を変換して平均0、分散1にしたものということです。
平均がμで分散がσの正規分布を、標準正規分布にするためには二つのステップが必要です。
①σを掛けて分散を1にする
②+μをして平均を0にする
以下の分布に①と②を行うことで平均0、分散1に変換できることがわかると思います。

正規分布から標準正規分布を導出する
それでは式で実際に導出していきましょう。
正規分布は、以下の式で表されます。
\(f_N(x)=\frac{1}{\sqrt{2π}σ}e^{\frac{(x-μ)^{2}}{2σ^2}}\)
以下標準正規分布を\(f_S(z)\)と表します。
先ほどの①を行うと、x→σzになります。
その後②を行うとx→σz+μとなるので、x=σz+μとなります。
また両辺を微分することで\(dx=σdz\)-①となります。
全ての確率を足すと必ず1になることから導かれる、\(\int_{∞}^{∞}f(x)dx=1\)-②という公式を用います。
①②より、\(\int_{∞}^{∞}f_S(z)dz=\int_{∞}^{∞}f_N(x)dx=\int_{∞}^{∞}f_N(σz+μ)σdz\)
よって\(f_S(z)dz=f_N(σz+μ)σdz\)より
\(f_S(z)dz=\frac{1}{\sqrt{2π}}e^{-\frac{z^2}{2}}\)
よって標準正規分布は以下の式で表されます。
\(f_S(z)dz=\frac{1}{\sqrt{2π}}e^{-\frac{z^2}{2}}\)
正規分布の問題点
最後に、標準正規分布を含めた正規分布の問題点についてです。
正規分布の問題点は以下です。
データの量が少ない場合は、外れ値の影響を大きく受けるため正規分布に従いづらい
正規分布は主にデータが多い場合に用いられ、少ない場合はあまり当てはまりが良いとはされません。
データが少ない場合は、データは違った分布になるので、次回以降でそちらについてまとめていきたいと思います。
まとめ
標準正規分布は、正規分布を標準化したもので以下で表される
\(f_S(z)dz=\frac{1}{\sqrt{2π}}e^{-\frac{z^2}{2}}\)
正規分布には、データの量が少ない場合は、外れ値の影響を大きく受けるため正規分布に従いづらいという問題点がある
今回はデータサイエンスに用いる統計4回目として、標準正規分布についてまとめました。
次回は、データの量が少ない場合にも用いることができるt分布についてまとめていきたいと思います!

最後まで読んでいただきありがとうございました。

他にもいろんな記事があるにゃ。



コメント