はじめに
どーも、将棋と筋トレが好きな学生エンジニアのゆうき(@engieerblog_Yu)です。
今回はデータサイエンスに必要な統計編3回目にして、最も重要となる正規分布について解説していきたいと思います!
過去の二項分布についても併せてどうぞ。
正規分布について
正規分布は、統計学の中で最も重要な働きをする連続型の確率分布です。
以下の式で表されます。
\(f_N(x)=\frac{1}{\sqrt{2π}σ}e^{\frac{(x-μ)^{2}}{2σ^2}}\)
意味が分からない式が出てきたな、、と思った方も多いと思います。
なぜこのような式が出てきたのかは、後ほど解説します。
グラフで表すと以下のようになります。
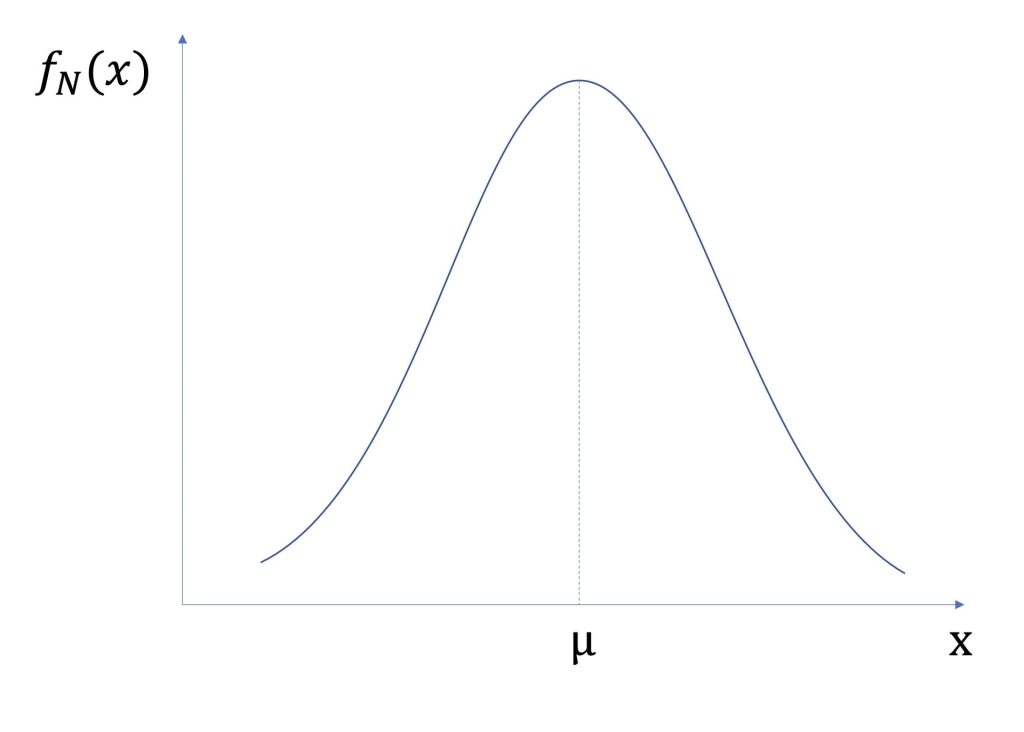
xが平均値μの時に極大値をとり、xが平均値μ周辺にある確率が高いことがわかると思います。
わかりにくいと思うので、一例として人間の体重で考えます。
20歳の男性の体重が正規分布に従うとして、平均値を50とすると、ほとんどの人が50kg付近に位置しています。
20kgや90kgの人の数は50kgの人と比べて、数が少ないということです。
(一例ですので数字はあてにしないでください。)
それでは次に、正規分布の導出についてまとめていきたいと思います。
正規分布は、最も重要な働きをする連続型の確率分布で、以下の式で表される
\(f_N(x)=\frac{1}{\sqrt{2π}σ}e^{\frac{(x-μ)^{2}}{2σ^2}}\)
(μとσは既に得られている値)
二項分布の試行回数nを無限大にしたものが正規分布となる
正規分布は、前回の記事でまとめた二項分布から導出することができます。
具体的にいうと二項分布の試行回数はnでしたが、n→∞にすることで正規分布になります。
実際にp=0.25として、二項分布が試行回数nを増やすとどうなるのか見ていきましょう。
n=10の時です。
2回成功する確率が0.28程度で最も高くなっていることがわかります。
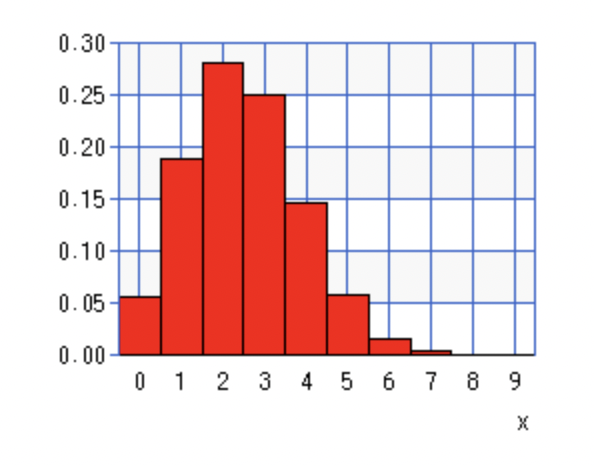
n=30の時です。7回成功する確率が0.17あたりになっています。
先ほどと比べて縦軸の値が小さくなっていて、より滑らかになっていることがわかります。
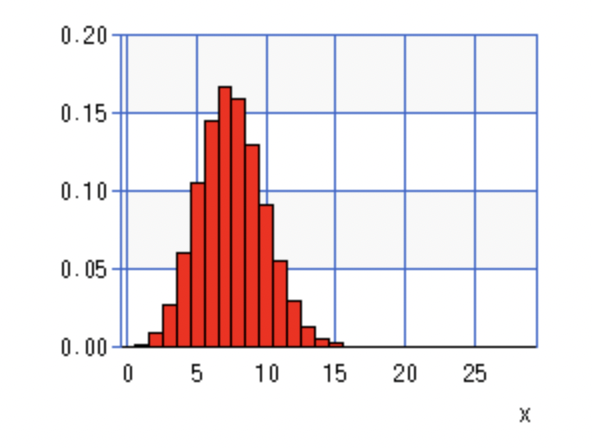
n=100の時です。
n=10の時と比べると、綺麗なすり鉢型に近づいていることがわかります。
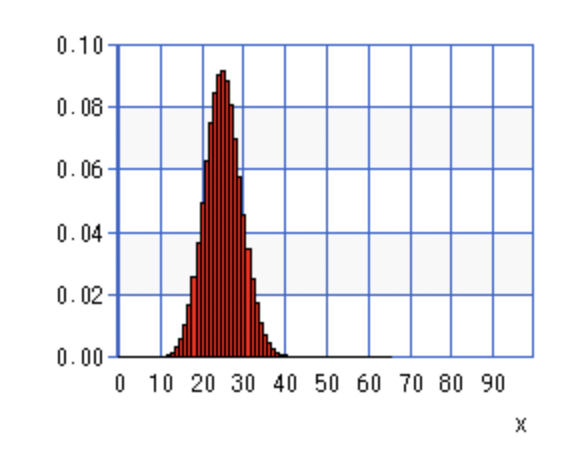
またこの時、n→∞だけでなくμ=np=一定でn→∞かつp→0とすると、ポアソン分布となります。
式での導出
ここからは具体的に式で導出していきたいと思います。
ざっくり理論だけ理解したい方は、読み飛ばしていただいても大丈夫だと思います。
二項分布は以下のように表されました。
\(P_b(x)={}_n C_x(p)^{x}(1-p)^{n-x}\)
これに対数をとったものをg(x)として、展開すると以下のようになります。
\(g(x)=log\frac{n!}{x!(n-x)!}p^x(1-p)^(n-x)\)
\(g(x)=logn!-logx!-log(n-x)!+xlogp+(n-x)log(1-p)\)
ここで、logx!の微分値はlogxに近似できることから、g'(x)は
\(g'(x)=-logx+log(n-x)+logp-log(1-p)\)
\(=log\frac{p(n-x)}{(1-p)x}\)
となります。
g'(x)=0となるxを計算すると、x=npとなります。
すなわちx=μに極大値をとるということが分かります。
(二項分布のμ=npを用いた。)
\(g'(μ)=0ー①\)
次にg”(x)を考えます。g”(x)は
\(g”(x)=-\frac{1}{x}-\frac{1}{n-x}=-\frac{n}{x(n-x)}\)
となり、x=μ=npを代入すると、
\(g”(μ)=-\frac{1}{np(1-p)}=-\frac{1}{σ^2}-②\)
となります。
ここで、g(x)をx=μでテイラー展開すると
\(g(x)=g(μ)+\frac{g'(μ)}{1!}(x-μ)+\frac{g”(μ)}{2!}(x-μ)^2+\frac{g^(3)(μ)}{3!}(x-μ)^3+・・\)
となります。
ここで、x≒μより、k=3,4・・の時、\((x-μ)^k=0\)とすると、3つの項だけを考えることができます。
\(g(x)≒g(μ)+\frac{g'(μ)}{1!}(x-μ)+\frac{g”(μ)}{2!}(x-μ)^2\)
ここで①②より
\(g(x)=g(μ)-\frac{1}{2σ^2}(x-μ)^2ー③\)
となり、③は以下のように表すことができます。
\(logP_b(x)≒logP_b(μ)+loge^{-\frac{1}{2σ^2}(x-μ)^2}\)
\(logP_b(μ)\)は定数ですのでcと表すと、
\(=logce^{-\frac{1}{2σ^2}(x-μ)^2}\)
となり、二項分布のnを大きくすると、以下のような確率分布に近づくことが分かります。
\(f_N(x)=ce^{-\frac{1}{2σ^2}(x-μ)^2}\)
最後に定数cを求めていきます。
全ての確率を足すと必ず1になることから導かれる、\(\int_{∞}^{∞}f_N(x)dx=1\)という公式を用います。
\(\int_{∞}^{∞}f_N(x)dx=1\)より
\(c\int_{∞}^{∞}e^{-\frac{1}{2σ^2}(x-μ)^2}dx=1\)
となります。
ここで\(z=\frac{x-μ}{σ}\)と\(\int_{∞}^{∞}e^{-\frac{z^2}{2}}dz=\sqrt{2π}\)を使ってあげると
\(c=\frac{1}{\sqrt{2π}σ}\)
となって
\(f_N(x)=\frac{1}{\sqrt{2π}σ}e^{\frac{(x-μ)^{2}}{2σ^2}}\)
を導出することができました。
なかなか大変でしたが、最後まで読んでいただけた方はお疲れ様です。
正規分布は重要な確率分布ですので、理解しておいて損はないと思います。
最後に正規分布で重要な68,95,99.7ルールについて、紹介していきます。
68,95,99.7ルール
正規分布には重要な68,95,99.7ルールというものがあります。
具体的には以下のようになります。
μ-σ < x < μ+σの範囲に68%のデータが入る
μ-2σ < x < μ+2σの範囲に95%のデータが入る
μ-3σ < x < μ+3σの範囲に99.7%のデータが入る
68%の場合をグラフにしたものが以下になります。
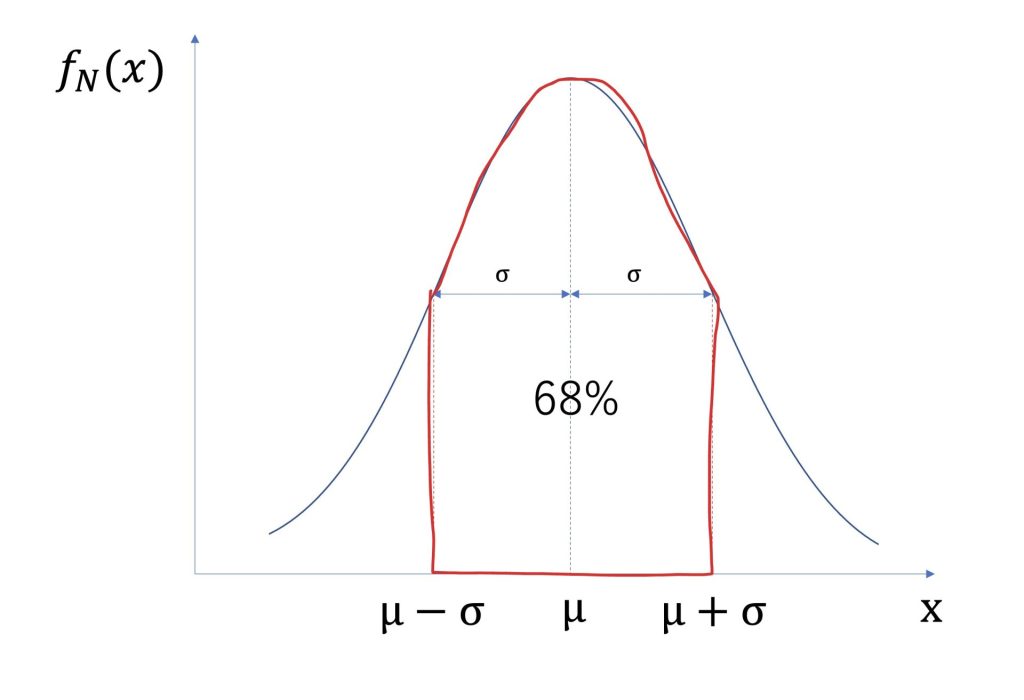
赤い線で囲った部分に全体の68%のデータが存在しています。
μ-3σ < x < μ+3σの範囲には、ほとんど全てのデータがあると言えます。
まとめ
正規分布は、最も重要な働きをする連続型の確率分布で、以下の式で表される
\(f_N(x)=\frac{1}{\sqrt{2π}σ}e^{\frac{(x-μ)^{2}}{2σ^2}}\)
正規分布は、二項分布の試行回数nを∞に近づけることで導出される
正規分布には、重要な68,95,99.7ルールがある
今回はデータサイエンスに用いる統計3回目として、最も重要な分布と言っても過言ではない正規分布についてまとめました。
次回は、正規分布を標準化した標準正規分布についてまとめていきたいと思います!

最後まで読んでいただきありがとうございました。

他にもいろんな記事があるにゃ。





コメント