どーも、情報系大学生のゆうき(@engieerblog_Yu)です。
今回は以下のような配列を昇順に並び替えていくことを考えていきます。
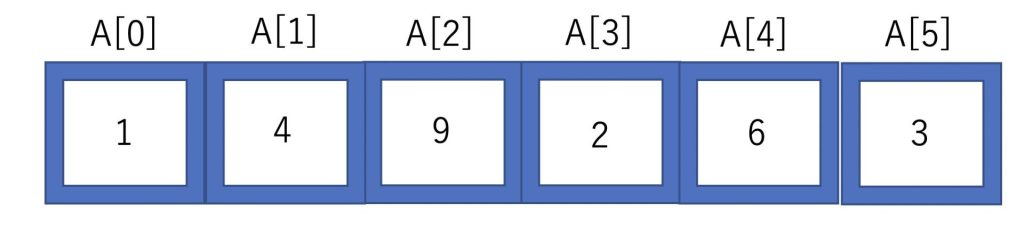
みなさんはどのように整列しようと考えるでしょうか?
整列の方法はいろいろありますが、どのような整列アルゴリズムを選ぶかで計算時間・計算量が変わってきます。
今回は色々な整列の方法をまとめましたので、ご参考にしていただけたら幸いです。
計算量のオーダー記法について怪しい方は、以下の記事を併せてどうぞ。
バブルソート・挿入ソート・シェルソート
まずはバブルソート・挿入ソート・シェルソートです。
バブルソートの計算量は最良O(n)、最悪O(n^2)、平均計算量O(n^2)
挿入ソートの計算量は最良O(n)、最悪O(n^2)、平均計算量O(n^2)
シェルソートの計算量はギャップ列に依存し、挿入ソートよりも小さくなることが多い
それぞれのアルゴリズムについては以下の記事で解説しています。
クイックソート・マージソート

次にクイックソートとマージソートについてです。
クイックソートの平均計算量はO(nlogn)、最悪計算量はO(n^2)
マージソートは平均計算量O(nlogn)、最悪計算量O(nlogn)
計算量がマージソートの方が小さいのでマージソートの方が良いアルゴリズムに思われがちですが、実際にはクイックソートの方が使われていることが多いです。
詳しくは以下の記事で解説しています。
ヒープソート

最後にヒープソートについてです。
ヒープソートはヒープの構築・最大値の削除の二つの段階に分けられる
ヒープの構築の計算量は、O(n)
最大値の削除は、O(nlogn)
ヒープソートの平均計算量はO(n)+O(nlogn)=O(nlogn)となる
具体的なアルゴリズムについては以下の記事で解説しています。
木構造について怪しい方は以下の記事をどうぞ。
整列アルゴリズムの平均計算量はO(nlogn)より小さくなることはない
整列アルゴリズムの平均計算量は、O(nlogn)より小さくすることができないことが証明されています。
よって平均計算量がO(nlogn)である、クイックソート、マージソート、ヒープソートは極めて優秀な整列アルゴリズムだと言えます。
終わりに

今回は整列アルゴリズムについて、まとめ記事を作成しました。
良いアルゴリズムを作成するという意識を持つだけでも、他の人と差をつけることができると思います。
私自身もアルゴリズムについては勉強中ですので、一緒に頑張っていきましょう。

最後まで読んでいただきありがとうございました。

他にもいろんな記事があるにゃ。








コメント