初めに
こんにちは。将棋と筋トレが好きな、情報系大学生のゆうき(@engieerblog_Yu)です。
今回は3種類の数値微分の手法を実装して比較していきたいと思います。
微分の定義(前方差分・中心差分・後方差分)
微分は一般的に以下の式で表されます。
\(\frac{df(x)}{dx}=\lim_{h→0}\frac{f(x+h)-f(x)}{h}\)
上記の式は、xの前方からx+hをxに近づけているので前方差分と呼ばれます。
図で表すと以下のようになります。
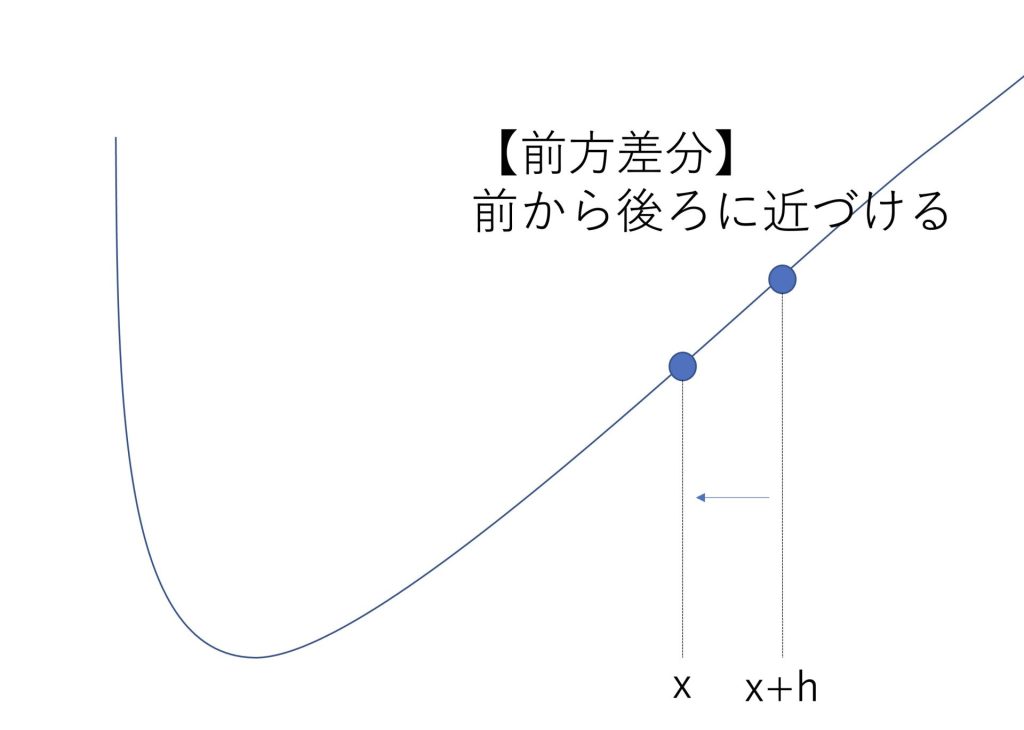
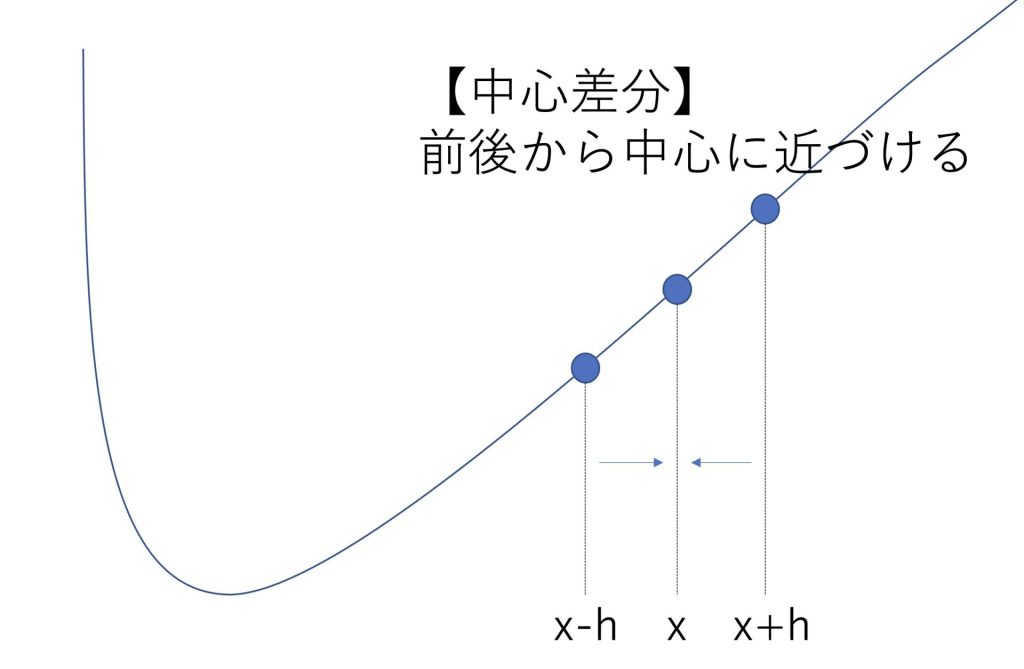
前方差分に対して、中心差分、後方差分もあります。
中心差分は以下の式で表されます。
\(\frac{df(x)}{dx}=\lim_{h→0}\frac{f(x+h)-f(x-h)}{2h}\)
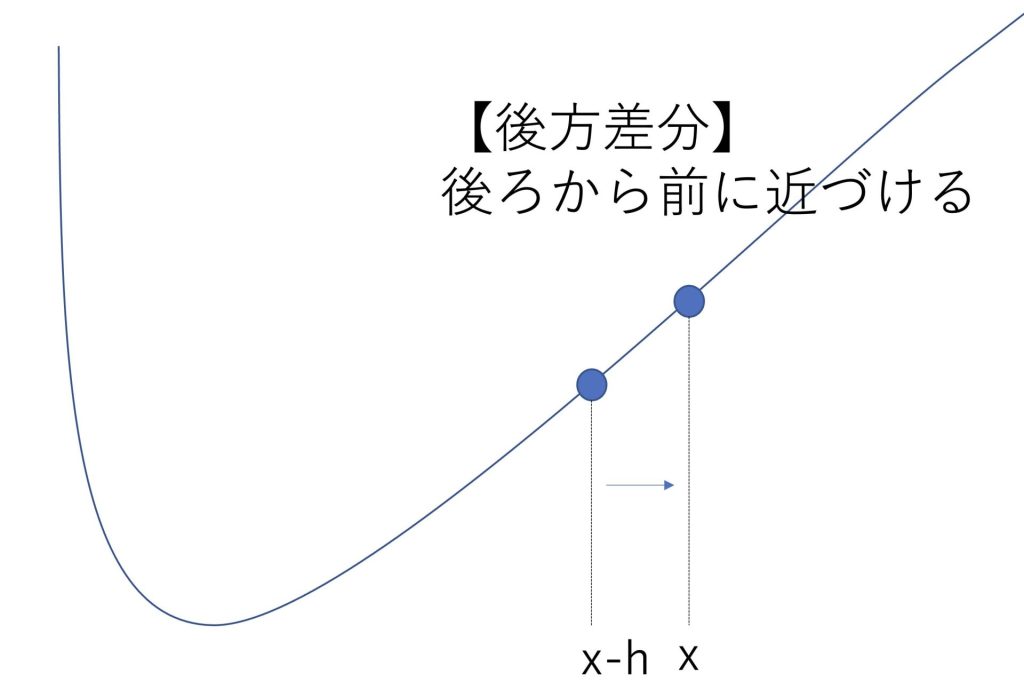
後方差分は以下の式で表されます。
\(\frac{df(x)}{dx}=\lim_{h→0}\frac{f(x)-f(x-h)}{h}\)
さてここである問題があります。
前方差分、中心差分、後方差分で求めた微分の値は同じであるのか?
ということです。
もちろん同じに決まってるじゃん!って思う方が多いと思います。
半分正解です。
確かに数学的に考えるのならば同じです。
しかしコンピュータで扱う上では、無限大、もしくは限りなく0に近い、という値を表現できないため誤差が発生します。
今回は前方差分、中心差分、後方差分、どれが最も誤差が小さくなるのかということについて調べたいと思います。
前方差分
\(\frac{df(x)}{dx}=\lim_{h→0}\frac{f(x+h)-f(x)}{h}\)
中心差分
\(\frac{df(x)}{dx}=\lim_{h→0}\frac{f(x+h)-f(x-h)}{2h}\)
後方差分
\(\frac{df(x)}{dx}=\lim_{h→0}\frac{f(x)-f(x-h)}{h}\)
微分をコンピュータで計算する場合は、限りなく0に近い値を使わなければいけないので、誤差が発生する
今回の関数
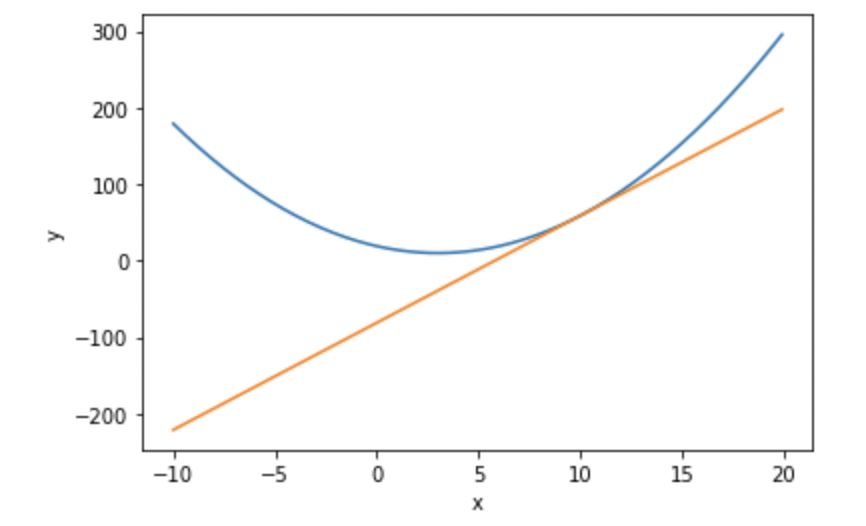
今回は\((x-3)^2+10\)という関数を用いて数値微分をおこなっていきます。
まずはどのような関数であるのかプロットしてみます。
def function(x):
return (x-3)**2 + 10import numpy as np
import matplotlib.pyplot as plt
x = np.arange(-10.0,20.0,0.1)
y = function(x)
plt.xlabel("x")
plt.ylabel("y")
plt.plot(x,y)
plt.show()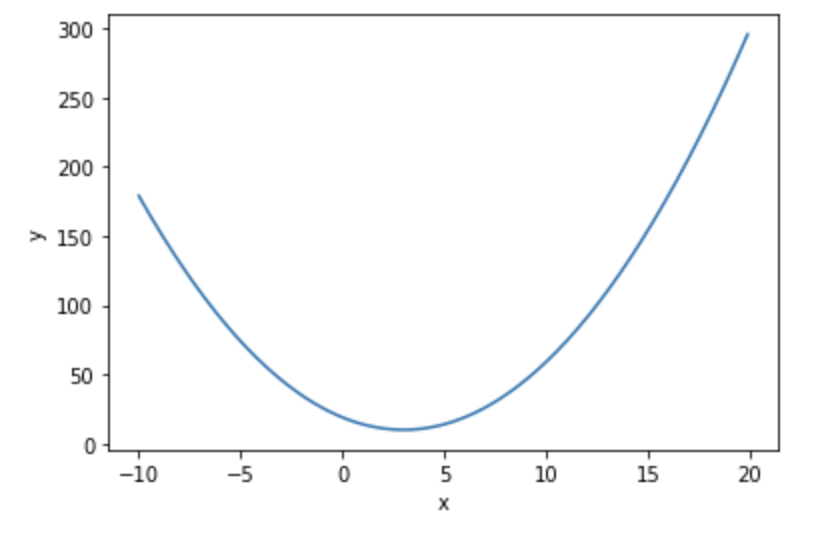
接線のプロット
今回はxが10の場合の微分の値を計算していきたいと思います。
\(\frac{∂f}{∂x}=2(x-3)\)となるのでx=10の微分値は14となるはずです。
以下は傾き14でx=10を通る接線をプロットした図です。
前方差分による数値微分
それでは数値微分をPythonで実装していきたいと思います。
hの値は小さすぎると、丸め誤差が発生してしまうので\(10^{-4}\)ぐらいの値がいいそうです。
# 前方差分
def numerical_diff(f,x):
h = 1e-4
return (f(x+h) - f(x)) / hprint(numerical_diff(function,10))微分値は以下のようになりました。
14.000099999975646# 誤差を出力
e = 14.0 - numerical_diff(function,10)
print(e)誤差は以下になります。
-9.999997564591467e-05中心差分による数値微分
次に中心差分を行なってみます。
# 中心差分
def numerical_diff(f,x):
h = 1e-4
return (f(x+h) - f(x-h)) / (2*h)print(numerical_diff(function,10))微分値は以下のようになりました。
13.999999999967372# 誤差を出力
e = 14.0 - numerical_diff(function,10)
print(e)前方差分よりも誤差が小さいことがわかります。
3.26281224261038e-11後方差分による数値微分
最後に後方差分で数値微分をおこなっていきます。
# 後方差分
def numerical_diff(f,x):
h = 1e-4
return (f(x) - f(x-h)) / hprint(numerical_diff(function,10))13.999899999959098# 誤差を出力
e = 14.0 - numerical_diff(function,10)
print(e)後方差分が最も大きい誤差になりました。
0.00010000004090215953今回実際に実装した結果中心差分が最も良い結果になりましたが、一般的にどのような関数でも中心差分が最も良い値になることがわかっています。
結果とまとめ
前方差分と中心差分と後方差分をコンピュータで実装すると、中心差分が最もいい結果になる
微分をコンピュータ上で行うと、限りなく0に近い値を使わなければならないので誤差が発生する
今回は数値微分の前方差分、中心差分、後方差分についてまとめました。
機械学習、ディープラーニングを学びたい方におすすめの入門書籍です。
ディープラーニングの理論が分かりやすくまとめられていて、力が身につけたい方におすすめです。

最後まで読んでいただきありがとうございました。

他にもいろんな投稿があるにゃ。


コメント