初めに
どーも、将棋と筋トレが好きな学生エンジニアのゆうき(@engieerblog_Yu)です。
今回から、データサイエンスに必要な確率統計の記事を書いていきたいと思います。
確率統計の基本から実践的な内容まで盛りだくさんの内容にするつもりですので、ぜひ見て頂けたら嬉しいです!
今回は、全ての分布の基本となる二項分布についてまとめていきたいと思います。
ベルヌーイ試行について
二項分布を導出するためにはベルヌーイ試行について理解する必要があります。
ベルヌーイ試行とは、一回の試行で二つの結果が起こりうる試行のことです。
例えば、
コインを投げて裏か表かを見る
サイコロを振って偶数が出るか奇数が出るか
投票結果が民主党か共産党か
といったようなものです。
一般に、確率が既知であるものや統計的に分かっているものに対してになります。
ベルヌーイ試行をグラフで表すと以下のようになります。
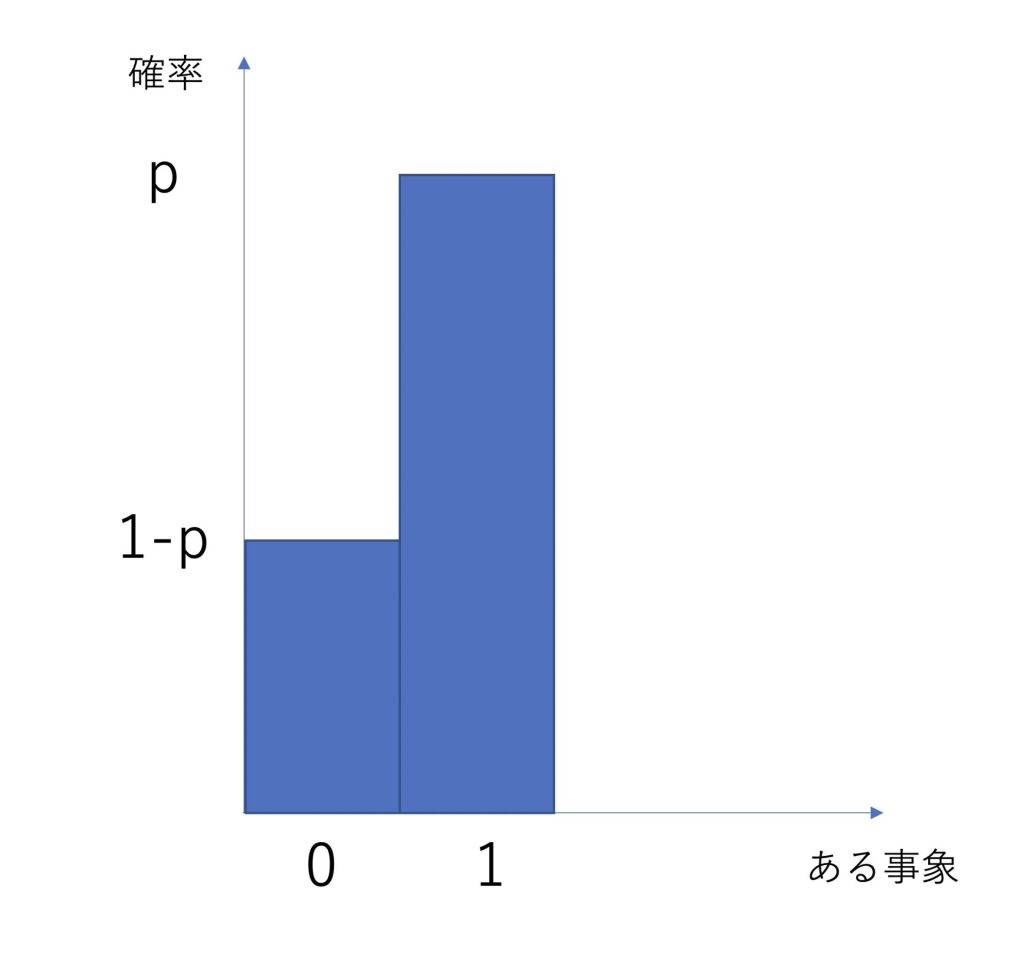
いびつなコインを使って、表が出る確率がpで、裏が出る確率が1-pになったとします。
表を1、裏を0とした場合に上記のようなグラフになります。
一般的に、発生する確率が高い方がp、事象は1にする決まりがあります。
今回は表の方が確率が高いとすると、表が1とpに対応します。
それでは、このようなベルヌーイ試行から、全ての分布の基本となる二項分布を導いていこうと思います。
二項分布(ベルヌーイ分布)について
二項分布は、ある結果を得るための確率を分布で表したものです。
例えばくじが入っていて、4回くじを引くことを考えます。
4回くじを引いて何回当たるかをグラフにしたものが以下になります。
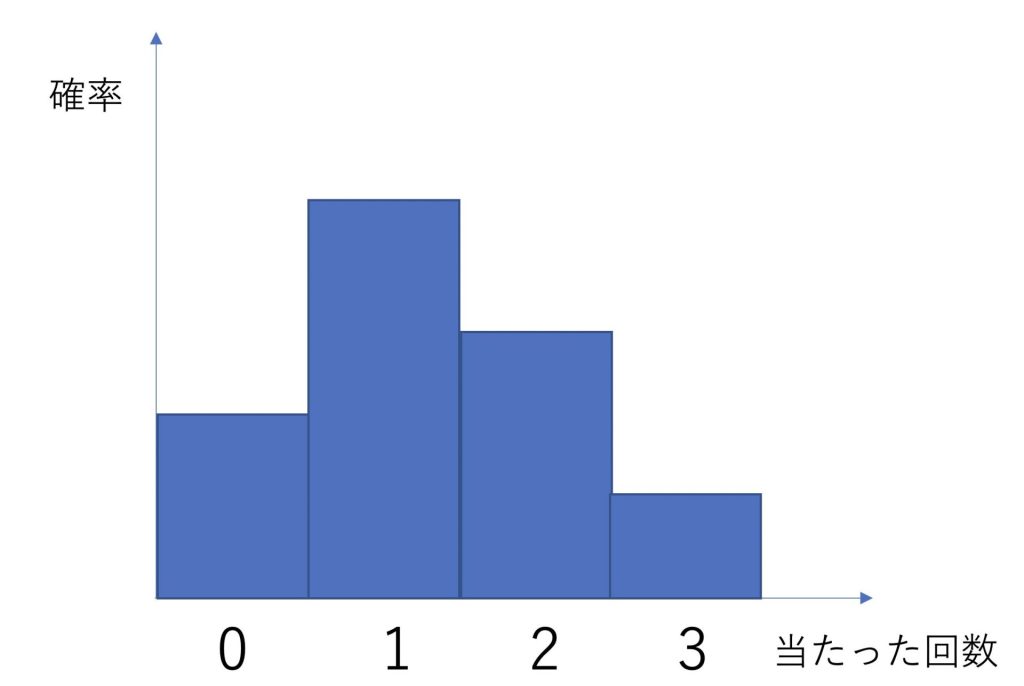
ベルヌーイ試行の場合は試行回数が1回でしたが、今回は試行回数が4回になっていることがポイントです。
一般にベルヌーイ試行を繰り返して、試行回数がn回の時を考えたものを二項分布と言います。
式で表すと、n回試行して、k回事象が起こる確率は
\(P_k={}_n C_k(p)^{k}(1-p)^{n-k}\)
となります。
先ほどの例だと、4回試行して、当たった数をkとすると
\(P_k={}_4 C_k(p)^{k}(1-p)^{4-k}\)
で表されるPの値が、先ほどのグラフの確率となります。
今回はヒストグラムのように凸凹している分布を扱いました。
これは横軸が離散的ですので、離散型確率分布と言われます。
補足ですが、二項分布の期待値はpn、分散はnp(1-p)で表されます。
まとめ
二項分布はベルヌーイ試行をn回繰り返したもので、以下の式で表される
\(P_k={}_n C_k(p)^{k}(1-p)^{n-k}\)
今回はデータサイエンスに用いる確率統計一回目として、二項分布を解説しました。
次回以降で、二項分布を基とした色々な確率分布についてまとめていきたいと思います!

最後まで読んでいただきありがとうございました。

他にもいろんな記事があるにゃ。





コメント