はじめに
こんにちは。将棋と筋トレが好きな、学生エンジニアのゆうき(@engieerblog_Yu)です。
今回はニューラルネットワークの隠的正則化についてまとめていきたいと思います。
隠的正則化とは?
ニューラルネットワークには、対象とする問題の複雑さに合わせてモデルの複雑さを制御するという性質があります。
そのような性質のことを隠的正則化と言います。
隠的正則化に対して、人為的に過学習を防ぐために正則化を行うことを明示的な正則化と呼びましょう。
隠的正則化と明示的な正則化を組み合わせることで、モデルの表現力を小さくし、過学習を防ぎ、汎化誤差を小さくすることができます。
今回はニューラルネットワークではどのような隠的正則化が行われているのかを3種類まとめていきたいと思います。
確率的勾配降下法によるノルム最小化
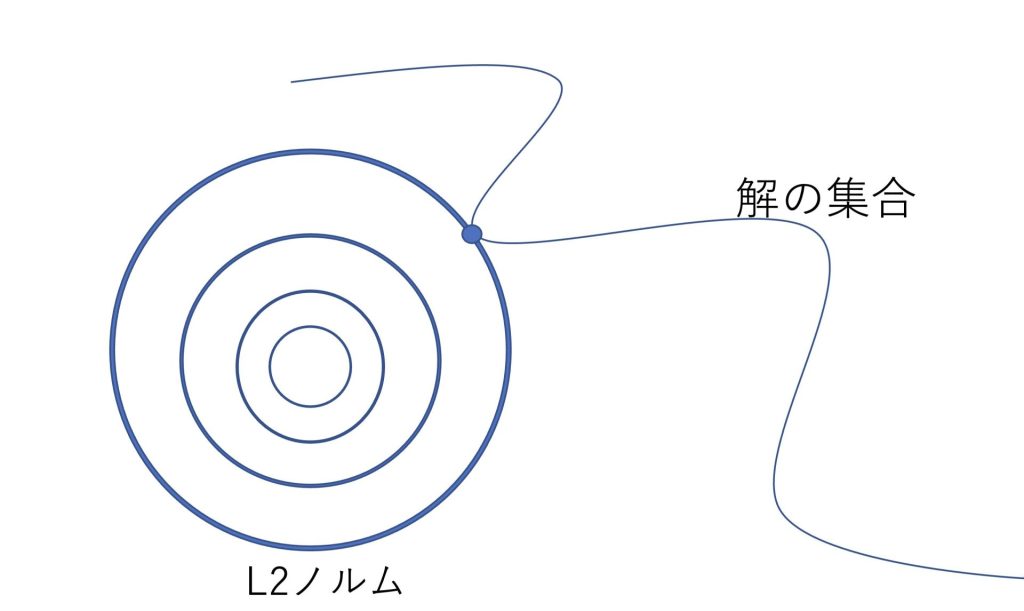
全てのデータではなく、一部のデータのみを使って勾配降下法を行うことを確率的勾配降下法(SGD)といいます。
確率的勾配降下法によって見つかる解は、L2ノルムが最小であり、低ランクであることが知られています。
以下参考文献です。
Surprises in High-Dimensional Ridgeless Least Squares Interpolation
https://arxiv.org/abs/1903.08560
ノルムが最小になることで、モデルの表現力が小さくなり、汎化性能が向上します。
また低ランクになることは、ニューラルネットワークの各層の行列演算が軽量化することを意味しているのでモデルの表現力が小さくなり、汎化性能も向上します。
確率的勾配降下法によって見つかる解は、L2ノルムが最小であり、低ランクである
解のノルムが最小で低ランクであることで、モデルの表現力が小さくなり、汎化性能が向上する
幅の広いニューラルネットワークで見つかる解がフラットであること
確率的勾配降下法で幅の広いニューラルネットワークを用いると、フラットな解を見つけることができるという性質があります。
フラットな解とは、損失関数を最小化した点付近の、損失関数の値も小さくなっている解のことをいいます。
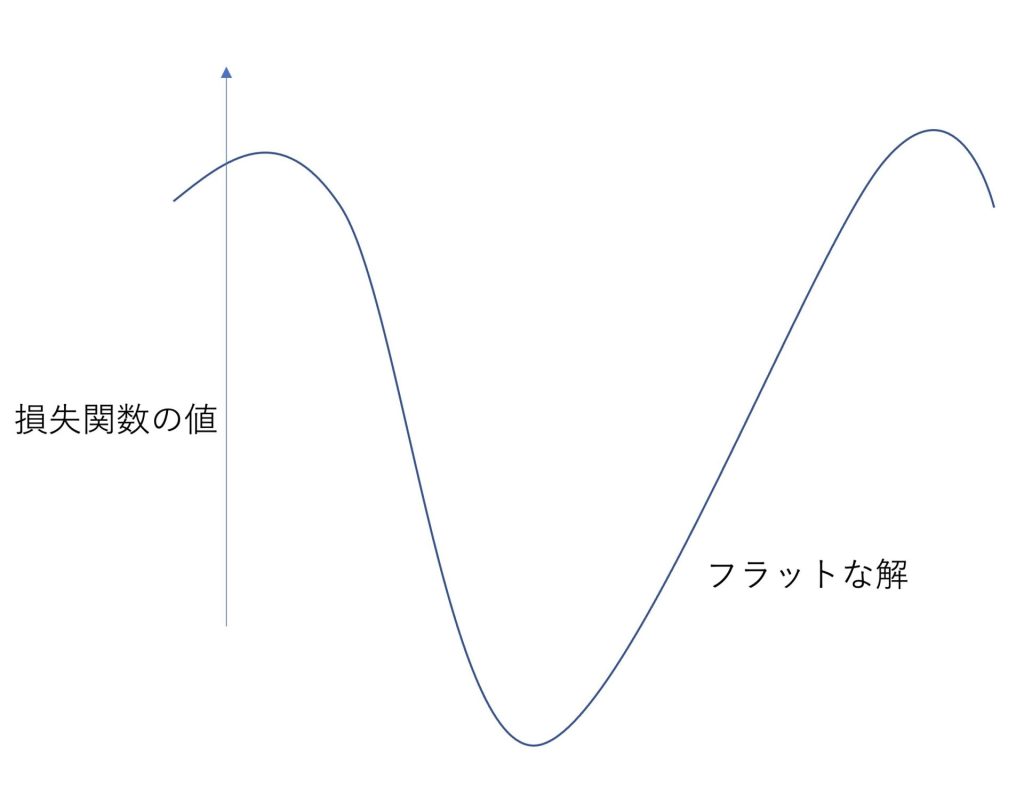
反対にシャープな解とは損失関数の値が、その付近で比較的に小さくなっていないもののことをいいます。
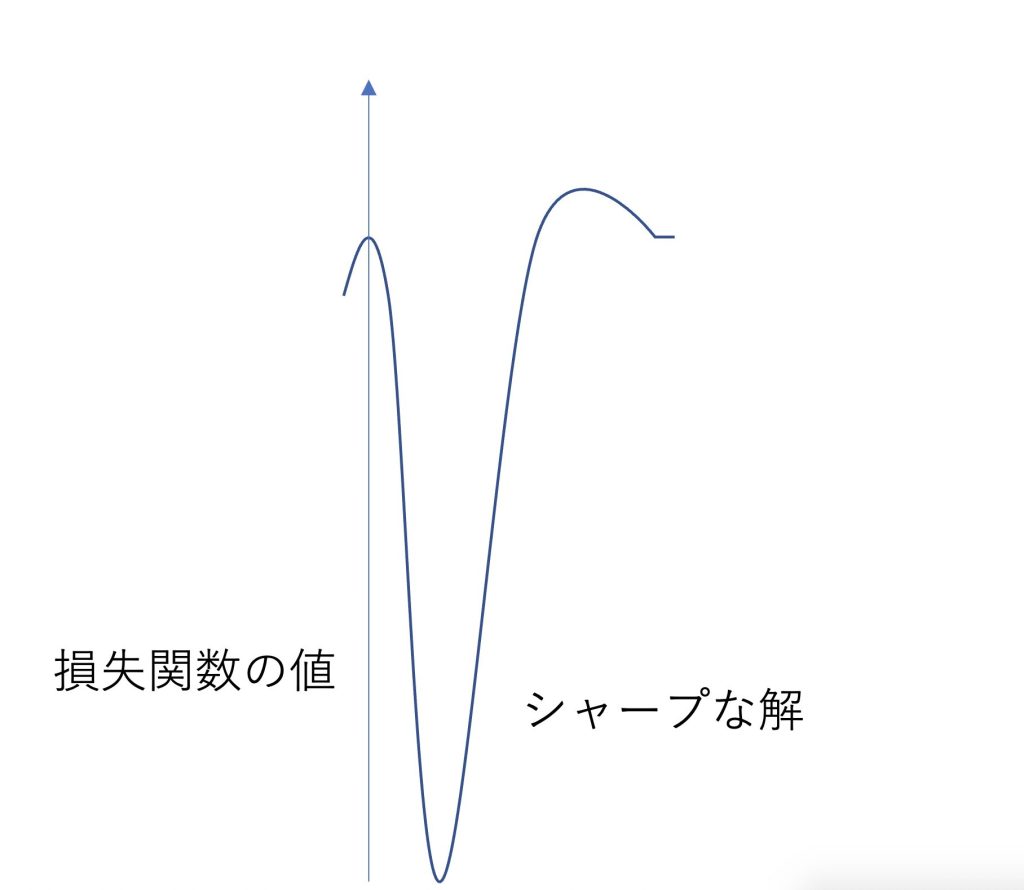
フラットな解であるほど、モデルが単純になり、シャープな解であるほどモデルが複雑になります。
シャープさを表すにはフラットな場合より、細かい部分を見なければいけないので、モデルもより複雑になるためです。
またフラットな解はノイズに強く、シャープな解はノイズに弱いといった性質があります。
これらのことから、フラットな解は汎化性能が高く、シャープな解は汎化性能が低いといえます。
フラットな解はモデルの表現力が小さく、ノイズに強く、汎化性能が高い
シャープな解はモデルの表現力が大きく、ノイズに弱く、汎化性能が低い
幅の広いニューラルネットワークで見つかる解は、フラットな解であることが知られている
宝くじ仮説
宝くじ仮説とは、ニューラルネットワークにはランダムに初期化されたネットワークと同じ学習精度を誇るサブネットワークを含まれているというものです。
例えば、以下のようなランダムに初期化されたニューラルネットワークがあったとします。
この中に、たまたま良い初期値の組み合わせを含んだサブネットワークがあったとします。
良い初期値の組み合わせのノードをオレンジ色で表しています。
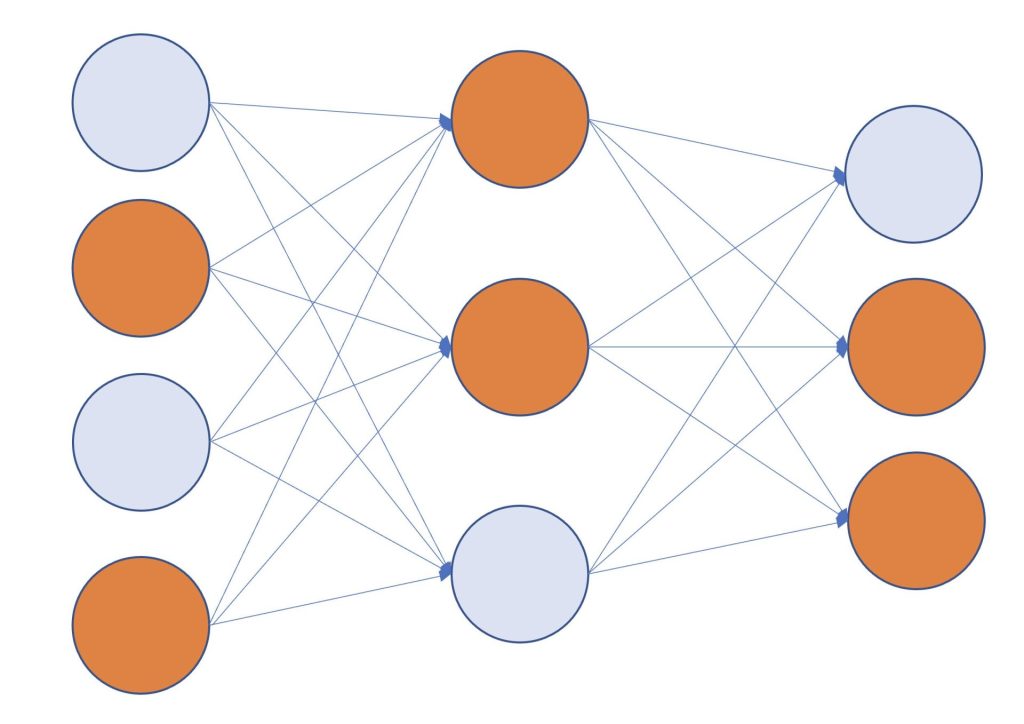
すると、最初のニューラルネットワークと、以下のようなサブネットワークの学習精度はほとんど同じになる、といったものが宝くじ仮説です。
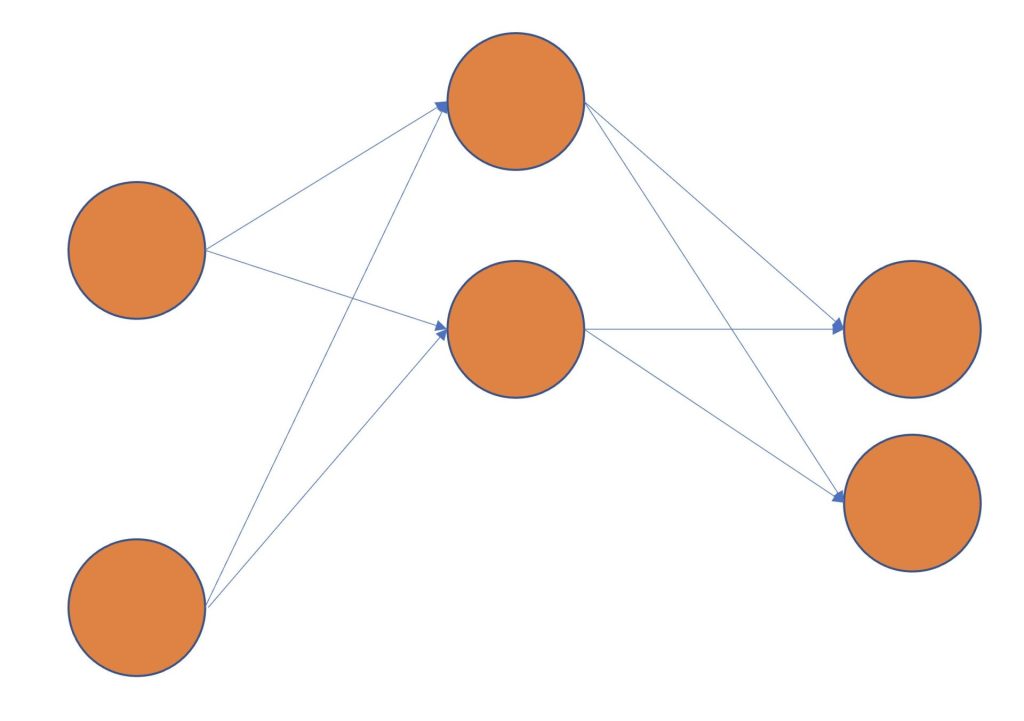
つまり宝くじ仮説は、ニューラルネットワークに偶然、当たりのサブネットワークが存在していた場合、サブネットワークのみの学習が進み、その他のネットワークは削られていくことが示唆されています。
つまり、ネットワークを大きくすると、過学習を起こしやすくなり汎化性能が低くなるのではなく、正解のサブネットワークが見つかりやすくなるといったことがいえます。
反対に、小さいネットワークでは、精度があまり良くないサブネットワークがたくさん見つかるため、汎化性能が低くなってしまいます。
以下宝くじ仮説が理論的に実証されている論文です。
The Lottery Ticket Hypothesis: Finding Sparse, Trainable Neural Networks
https://arxiv.org/abs/1803.03635
宝くじ仮説とは、ニューラルネットワークには、ランダムに初期化されたネットワークと同じ学習精度を誇るサブネットワークを含まれているという仮説
ネットワークを大きくすればするほど、過学習を起こしやすくなるのではなく、正解のサブネットワークが見つかりやすくなる
宝くじ仮説は理論的に実証されてきている
まとめ
ニューラルネットワークには自動でモデルの複雑さを制御する隠的正則化が備わっている
隠的正則化にはノルム最小化、解がフラットである性質、宝くじ仮説の三つがある
今回はニューラルネットワークの隠的正則化についてまとめました。
機械学習、ディープラーニングを学びたい方におすすめの入門書籍です。
ディープラーニングの理論が分かりやすくまとめられていて、コーディングしながら力を身につけたい方におすすめです。

最後まで読んでいただきありがとうございました。

他にもいろんな投稿があるにゃ。





コメント