目次
はじめに
どーも、将棋と筋トレが好きな学生エンジニアのゆうき(@engieerblog_Yu)です。
今回は簡単にサロゲートモデルを構築することができる、Surrogate Modeling Toolbox(SMT)というライブラリがあったので、そちらについて紹介していきたいと思います!
上記のURLのGitHubのコードを参考にさせていただきました。
ラテン超方格サンプリング(LHS)について
まずはサロゲートモデルを作成するためのデータセットについてです。
どうやら今回は、LHSというアルゴリズムでランダムサンプリングしているようです。
LHSの主なアルゴリズムは以下になります。
サンプリング点数に合わせた格子を生成してから、その格子を行と列が一致しないように選び、その中でランダムサンプリングする
例えば、三個の点をサンプリングしたい場合、以下のように領域を3×3に分割します。
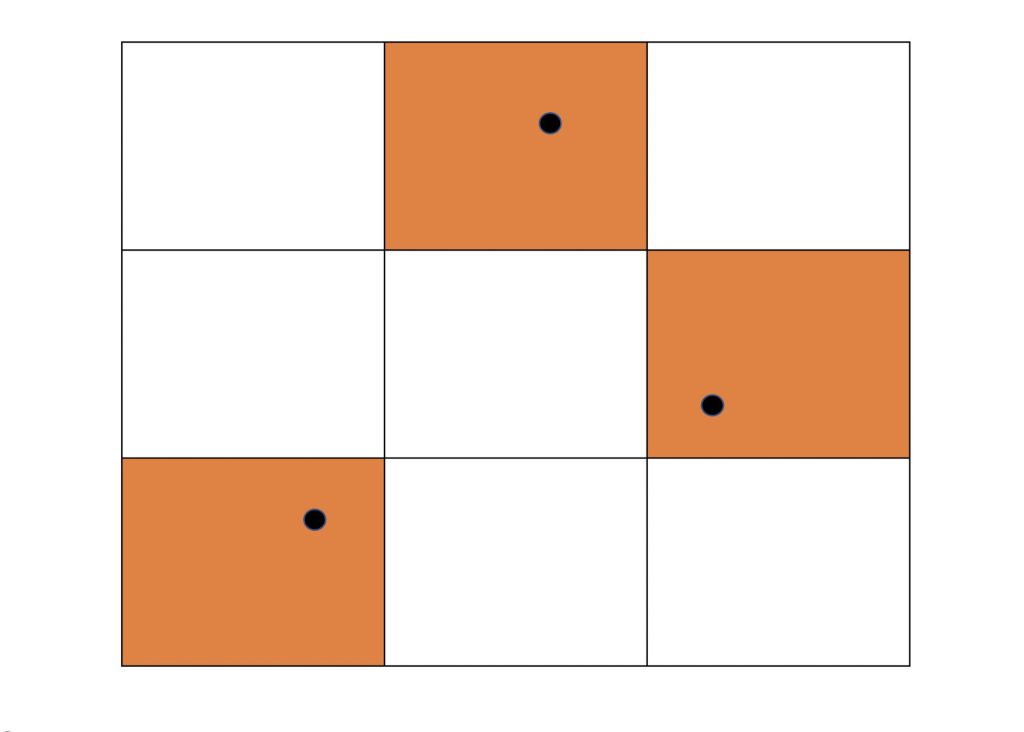
その時分割した格子は行と列が一致しないように選択しなければなりません。
そのように選ばれた格子領域の中から、ランダムで点をサンプリングします。
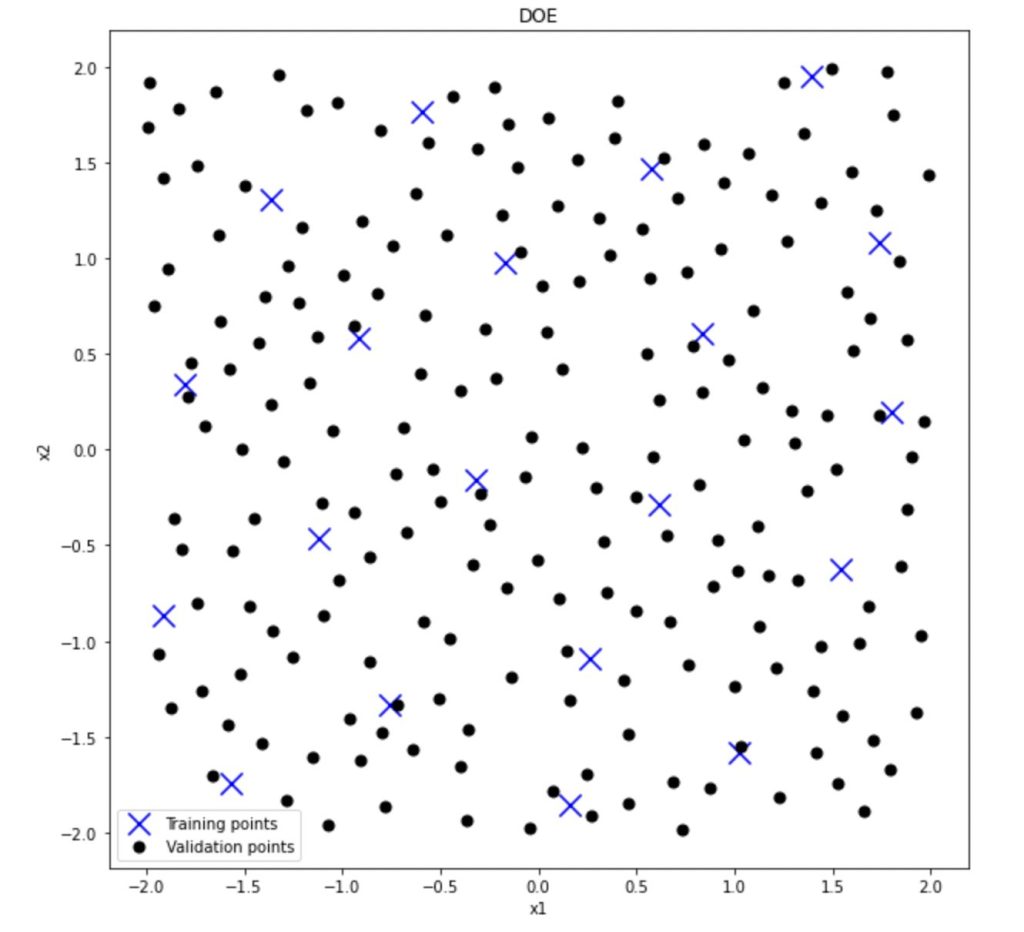
以下の画像のように、今回サロゲートモデルの訓練に用いるTraining dataは20点、学習済みのサロゲートモデルの評価に使うValidation dataは200点でサンプリングしているようです。
Rosenbrock Function in dimension Nについて
今回は非線形関数の最適化問題によく使われるRosenbrock関数を用いていきます。
Rosenbrock functionは、N次元で以下のように表されます。
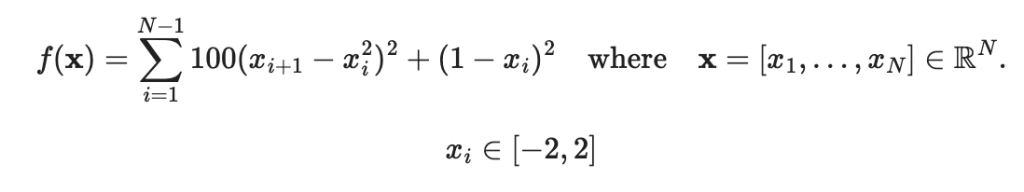
今回は二次元ですので、以下の式になります。
\(f(x)=100(x_2-x_1)^2+(1-x_1)^2\)
先ほどのLHSアルゴリズムによって生成された、二次元平面上の点それぞれに対してRosenbrock Functionを計算したものをz軸として、プロットしたものが以下です。
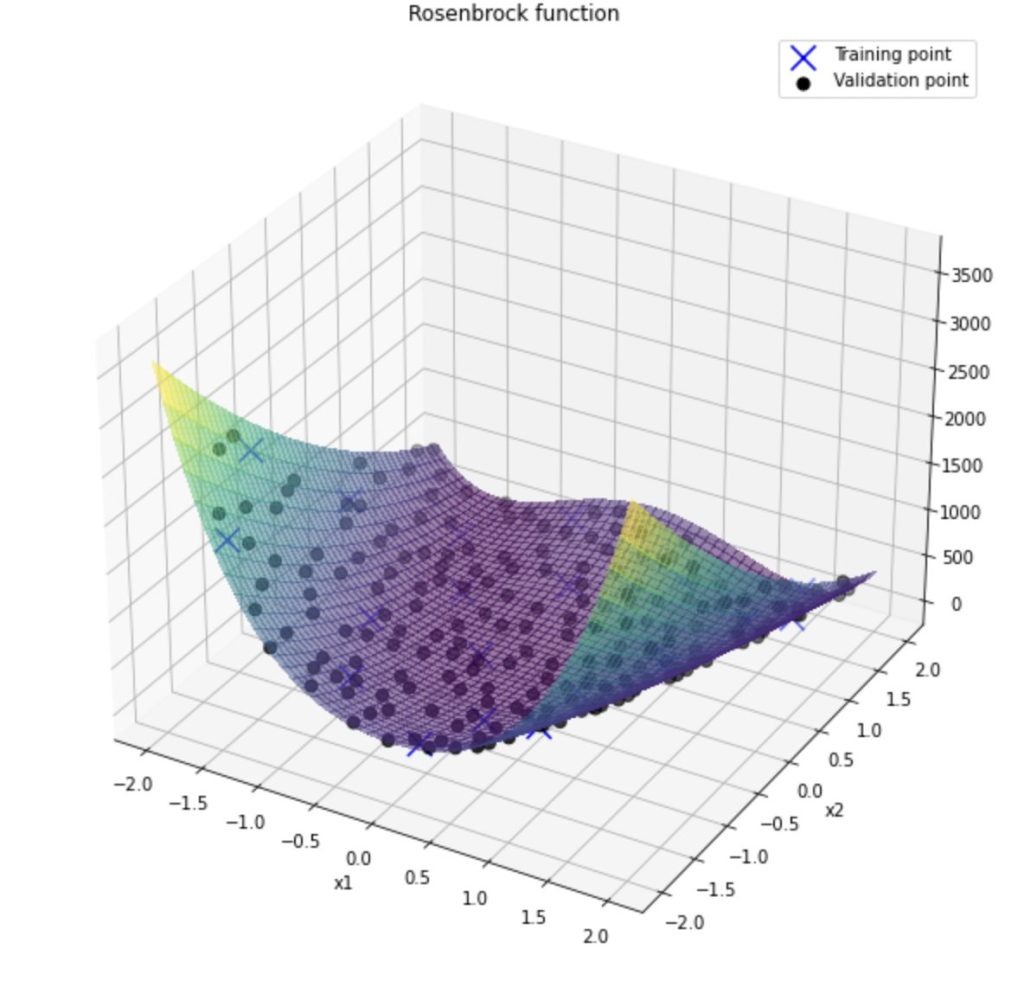
今回は青点のTraining pointだけを用いて、上記の曲面に近いものを表現できるサロゲートモデルを作成していきます。
今回は、以下の三つの回帰アルゴリズムを選択したサロゲートモデルを構築していきます。
Linear Model(線形回帰モデル)
Quadratic Model(二次回帰モデル)
Kriging Model(ガウス過程回帰モデル)
Linear Model(線形回帰モデル)
まずは線形モデルを学習します。
3次元の線形モデルですので、板のような形をしたモデルを作成しているというイメージです。
結果は以下のようになります。
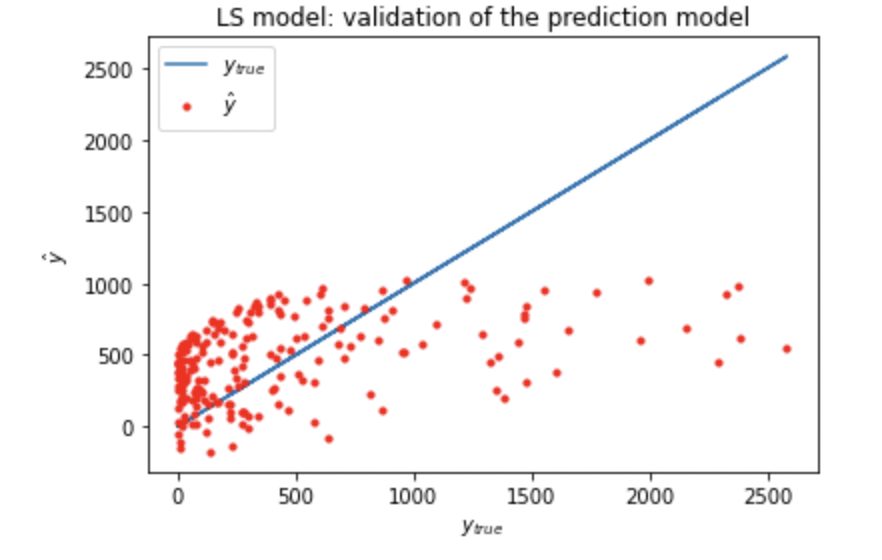
\(\hat{y}\)はyの予測値となります。
\(\hat{y}=y_{true}\)となった時、モデルの精度が100%になるということになります。
線形モデルはかなりの誤差があることが見てとれます。(曲面を板で表現しようとしているので当たり前ですが)
Quadratic Model(二次回帰モデル)
次は二次モデルを学習します。
先ほどは板でしたが、次は瓦のような形をしたモデルです。
結果は以下のようになります。
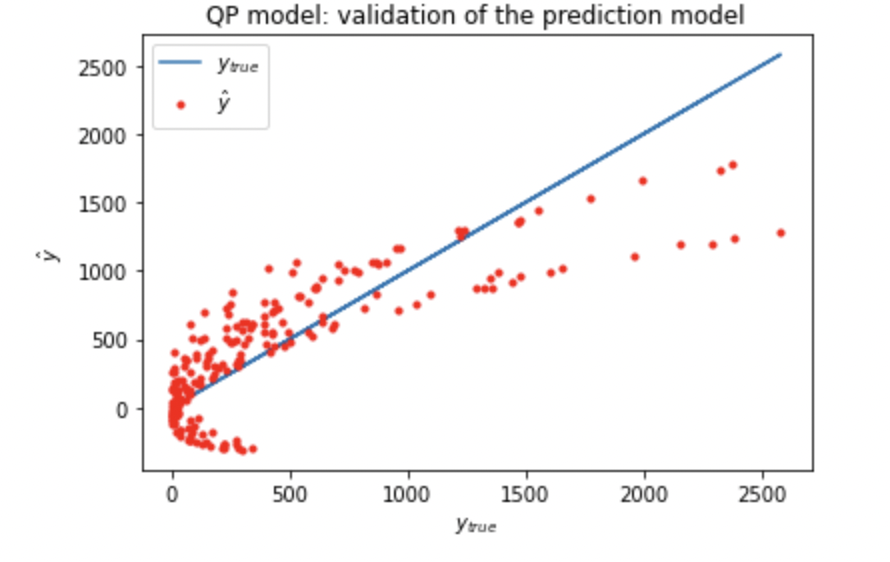
先ほどよりはいい感じですが、まだまだ正解には程遠いといったような感じですね。
Kriging model(ガウス過程回帰モデル)
ガウス過程回帰とは線形回帰モデルを、カーネルトリックというテクニックを用いて非線形の回帰モデルに変換する手法です。
ガウス過程回帰を、とても分かりやすくまとめてくれていたサイトがあるのでそちらも合わせてどうぞ。
ガウス過程回帰(Gaussian Process Regression, GPR)~予測値だけでなく予測値のばらつきも計算できる!~
結果は以下のようになります。
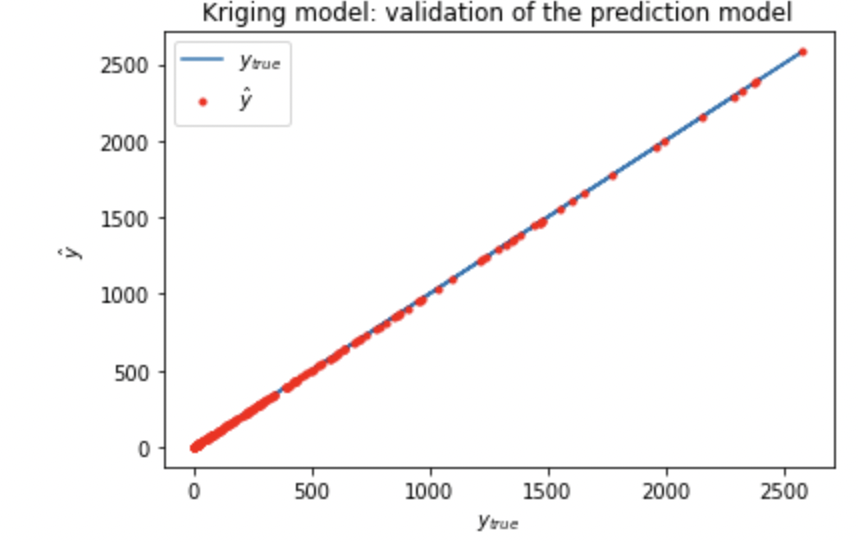
かなり高い精度のサロゲートモデルを作成することができていることが分かります。
三次元空間に、ガウス過程回帰ベースのサロゲートモデルをプロットしてみると以下のようになります。
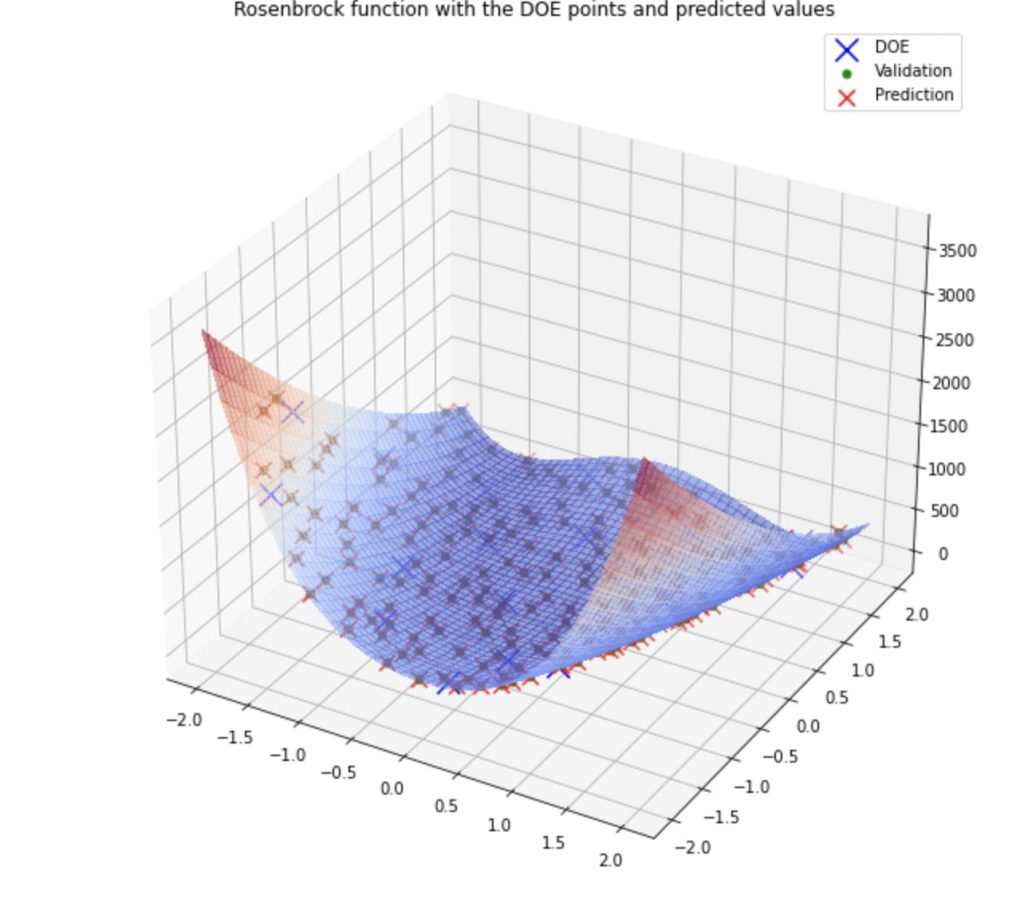
青の正解データと赤の予測値が似た形になっていることが分かります。
今回の内容のコードは、SMT_Tutorial.ipynbから実行することができるのでぜひ実行してみてください!
今回紹介した回帰アルゴリズム以外で学習した、サロゲートモデルも紹介されています。
終わりに
今回はSMTライブラリを使って、簡単なサロゲートモデルを構築する方法についてまとめました。
研究や仕事などでサロゲートモデルを使う方にとって、有益な情報となれば幸いです。

最後まで読んでいただきありがとうございました。



コメント