目次
はじめに


こんにちは。学生エンジニアのゆうき(@engieerblog_Yu)です。
今回はscikit-learnというデータ分析のライブラリのランダムフォレストを用いてタイタニック号の生存者予測を行っていこうと思います。
今回の記事をお勧めする方は
データ分析に興味がある
scikit-learnを使ってみたい
機械学習を使って分類問題を解いてみたい
kaggleに挑戦したい
と思っている人です。

気が向いたら頑張るにゃ。
ランダムフォレストとは?

ランダムフォレストとは教師あり学習の分類問題に使われるアルゴリズムです。
教師あり学習は以下の二つに分けられます。
教師あり学習
・回帰問題
・分類問題←今回
教師あり学習につきましては過去にも記事を出しています。
教師なし学習につきましても以下の二つに分けられます。
教師なし学習
・クラスタリング
・次元削減
こちらも過去に記事を出しています。
次にランダムフォレストのアルゴリズムを理解するための決定木のアルゴリズムについて説明していきたいと思います。
決定木のアルゴリズム

ランダムフォレストを理解するには決定木についての理解が不可欠です。
例えば生存確率に年齢と体重が関係あったとします。(不快に思われる方がいたら申し訳ありません、、、。)
例えば以下のような図です。
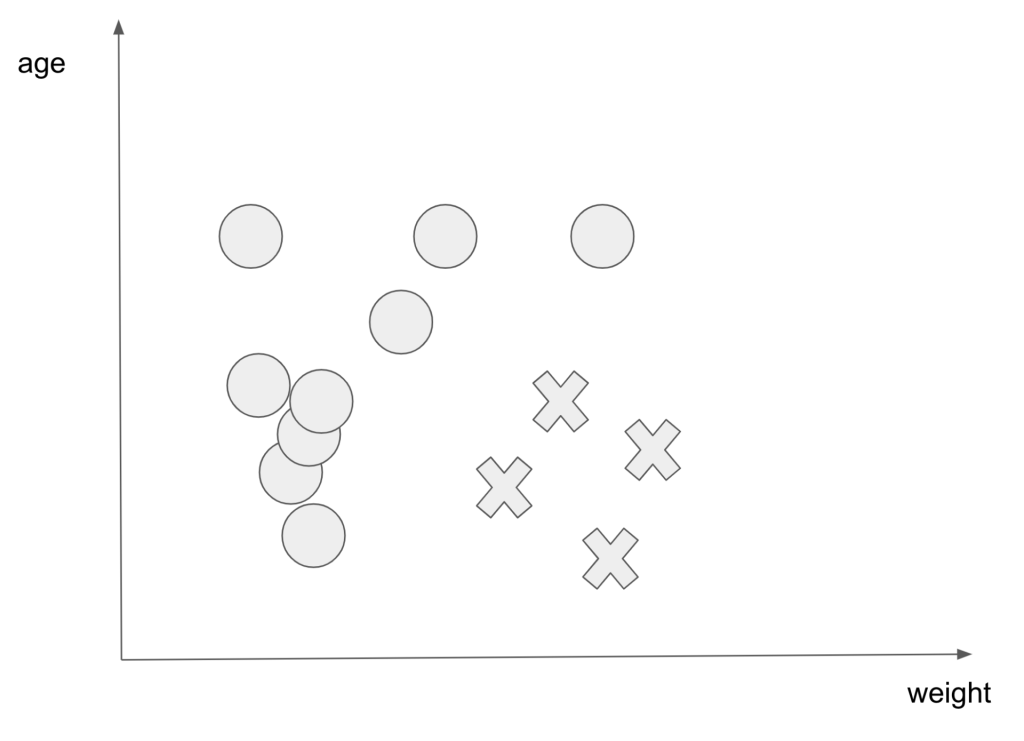
○が生存者で×が死亡者を表しています。
上記の図を見ると体重と年齢で生存確率が変わってきそうだということが直感的にわかると思います。
次に直感ではなく数値的に表してみます。
以下の図を見ると年齢が50以下で体重が80以上の範囲の人が死亡していることがわかります。
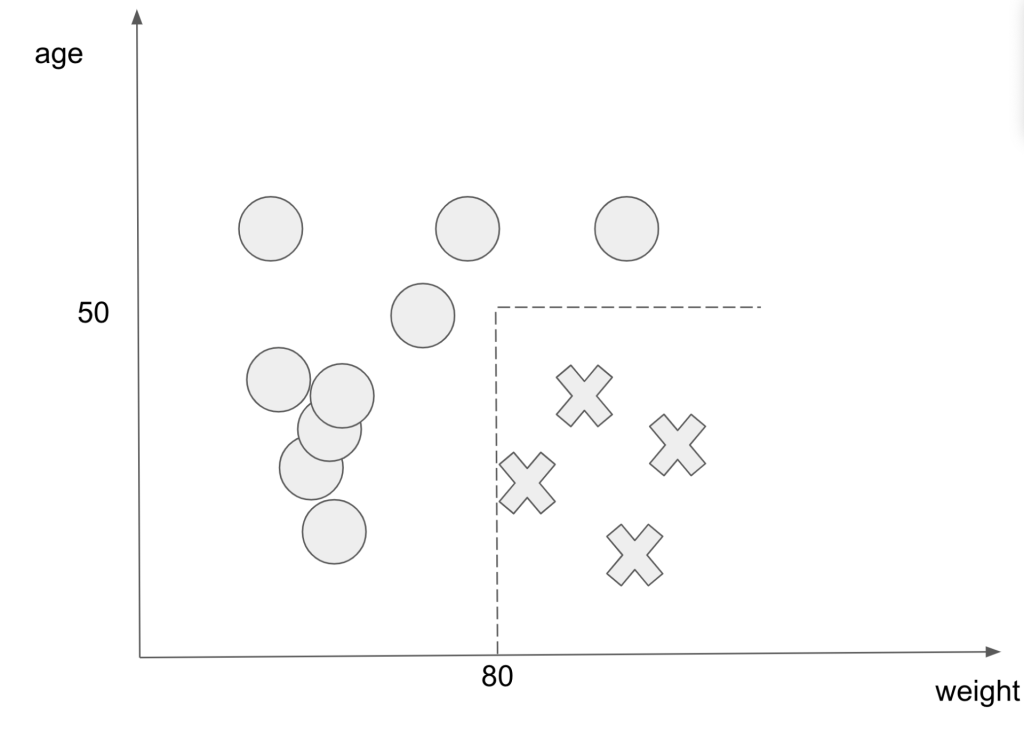

点線の範囲はどうやって決めるのにゃ?
最適な点線の範囲を決めるためにはジル係数やエントロピーなどの指標が用いられます。
これらの指標はデータの不純度を定量化することができます。

データの不純度とは同じ区間に○と×が入っている割合のことです。
ジル係数の場合はジル係数の値が0になった場合、データの不純度が最小になり、決定木の作成が完了します。
上記の作業を決定木で表したものが以下の図です。
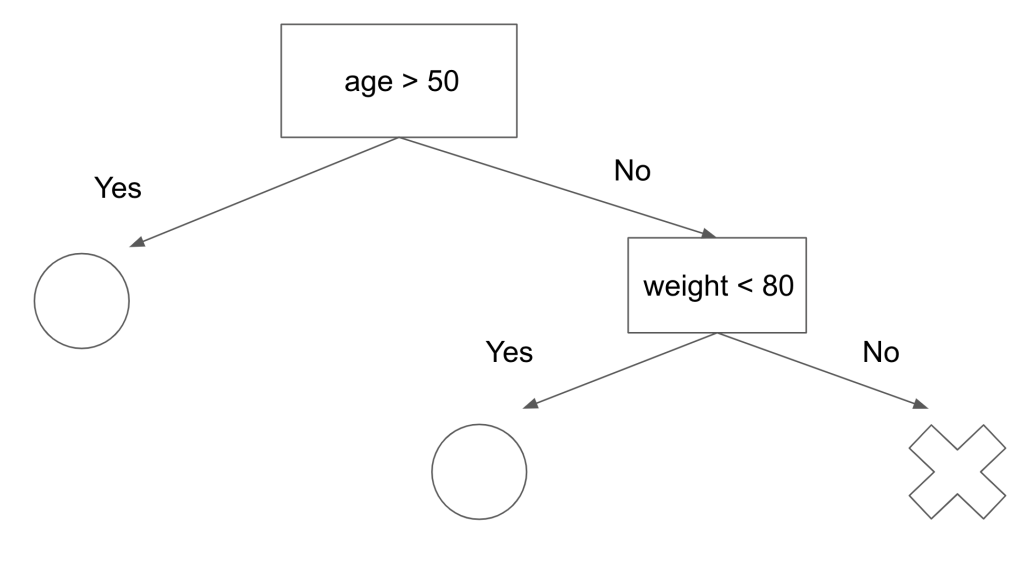
決定木はこのように作成されるモデルです。
決定木はジル係数やエントロピーによって定量化された後に最適な区切り方を学習したモデル

しかし決定木には問題があります。
決定木は最適な区切り方を学習することで過学習を起こすことがあります。
よって訓練データに当てはまりが良いモデルを作成できても、テストデータに当てはまりが良いモデルだとは言えないことがあります。
そのような過学習を防ぐためにランダムフォレストを使います。
ランダムフォレストについて

それでは今回用いるランダムフォレストについてです。
ランダムフォレストは先ほどのような決定木を大量に作成して多数決をとる方法です。
大量の決定木を作成する際に、同じデータを用いては意味がないので、データサンプルを水増ししたり、特徴量をランダムに選択したりします。
データサンプルを重複ありで抽出するなどして水増しすることはブートストラップと呼ばれています。
ランダムフォレストとはブートストラップ や特徴量をランダムに選択したりして決定木を大量に作成して多数決をとる手法

それでは実際にタイタニック号の生存者予測を行っていきましょう!
使用するライブラリ

今回使用するライブラリは以下です。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import RandomForestClassifier使用するデータセット

今回はkaggleというデータ分析コンペで配布されているデータセットを使います。
以下のリンクからダウンロードしたtrain.csvとtest.csvを実行ファイルと同じディレクトリにおきます。
Titanic – Machine Learning from Disaster
train = pd.read_csv('./train.csv')
test = pd.read_csv('./test.csv')trainデータを見てみるとしっかりデータが読み込まれていることがわかります。
| pclass | 客室のグレード |
| survival | 生存しているか |
| name | 名前 |
| sex | 性別 |
| age | 年齢 |
| sibsp | 乗客の兄弟姉妹と配偶者 |
| parch | 乗客の親と子供 |
| ticket | チケット |
| fare | 運賃 |
| cabin | 船室 |
| embarked | 乗船した港 |
| boat | ボート番号 |
| body | 識別ナンバー |
| home.dest | 目的地 |
欠損値の確認と補完

次にデータの欠損を確認します。
def MissVal_table(df):
null_val = df.isnull().sum()
percent = 100 * df.isnull().sum()/len(df)
MissVal_table = pd.concat([null_val, percent], axis=1)
MissVal_table_ren_columns = kesson_table.rename(
columns = {0 : '欠損数', 1 : '%'})
return MissVal_table_ren_columns上記で定義した関数を使って訓練データ、テストデータの欠損を確認してみます。
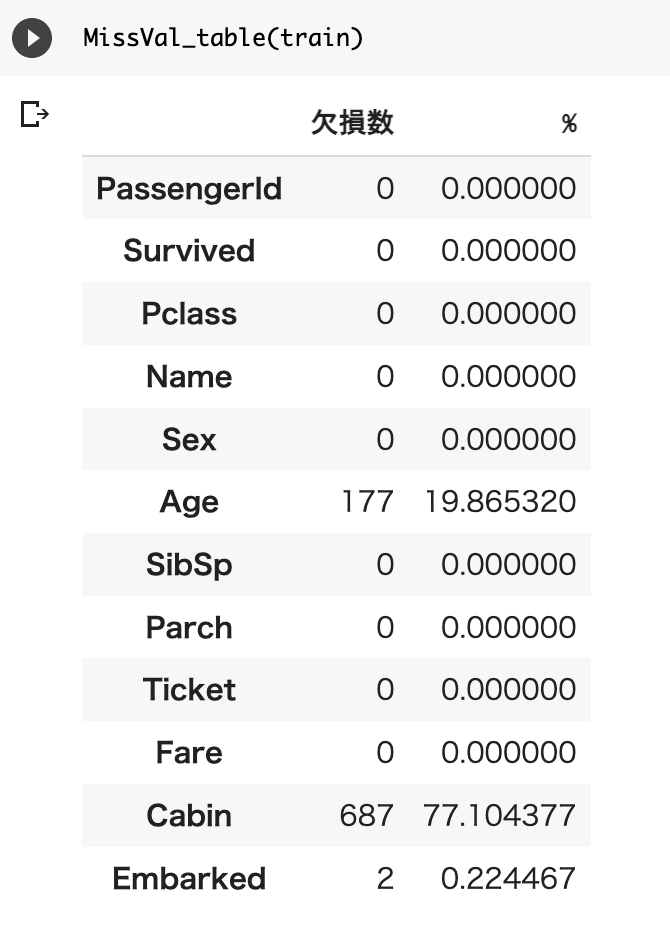
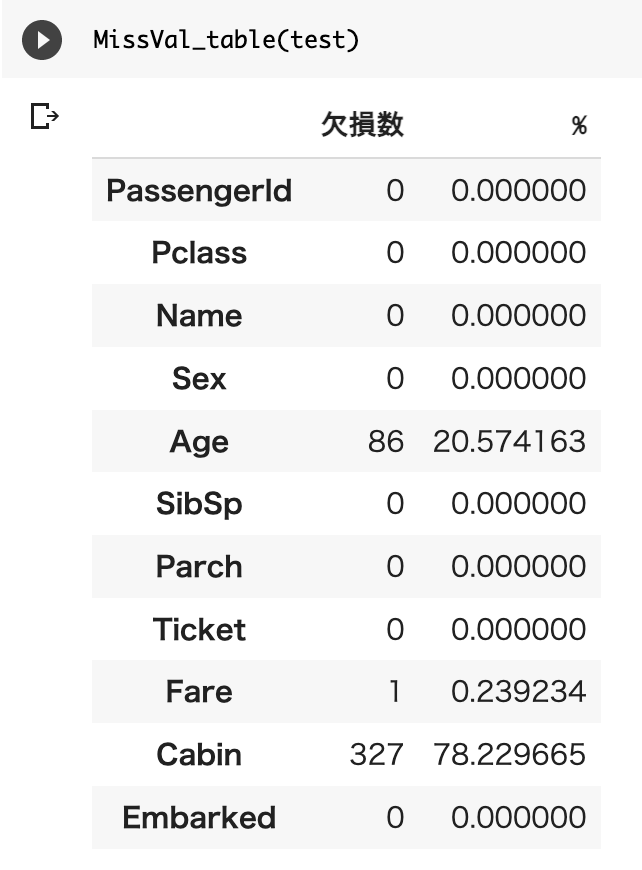

AgeとCabinとFareに欠損があるのがわかります。
ここから欠損値の補完を行っていきます。
欠損値の補完はモデルの精度を分ける大事な作業です。
今回は簡単のために年齢と運賃は中央値、乗船地は一番多かったSを用いました。

欠損値の補完は多くの議論がなされています。
train["Age"] = train["Age"].fillna(train["Age"].median())
train["Embarked"] = train["Embarked"].fillna("S")
test["Age"] = test["Age"].fillna(test["Age"].median())
test.Fare[152] = test.Fare.median()欠損値を確認し、ある場合は補完する(どのように補完するかが重要)
ダミー変数への変換

次にダミー変数への変換を行います。
文字列をモデルに用いることはできないので男→0、女→1などのようにして数値におき変えたものをダミー変数と言います。
train["Sex"][train["Sex"] == "male"] = 0
train["Sex"][train["Sex"] == "female"] = 1
train["Embarked"][train["Embarked"] == "S" ] = 0
train["Embarked"][train["Embarked"] == "C" ] = 1
train["Embarked"][train["Embarked"] == "Q"] = 2test["Sex"][test["Sex"] == "male"] = 0
test["Sex"][test["Sex"] == "female"] = 1
test["Embarked"][test["Embarked"] == "S"] = 0
test["Embarked"][test["Embarked"] == "C"] = 1
test["Embarked"][test["Embarked"] == "Q"] = 2文字列をダミー変数に置き換える
訓練用データとテストデータの作成

それでは訓練用データとテストデータを作成します。
今回は特徴量として使えそうな値を7つピックアップしました。
# 訓練用データ
X_train = train[["Pclass", "Sex", "Age","SibSp","Parch", "Fare","Embarked"]].values
X_test = test[["Pclass", "Sex", "Age","SibSp","Parch", "Fare","Embarked"]].values
# テスト用データ
y_train = train["Survived"].valuesランダムフォレストモデルの作成

それではランダムフォレストのモデルを作成していきましょう。
#ランダムフォレストモデルの作成
model = RandomForestClassifier(bootstrap=True,n_estimators=10,criterion='gini',max_depth=None,random_state=1)
model.fit(X_train,y_train)| bootstrap | ブートストラップの有無 |
| n_estimators | 決定木の数 |
| criterion | ジニ係数、エントロピーなど不純度の指標 |
| max_depth | 決定木の深さ |
| random_state | 乱数のシード数 |
#テストデータの生存者を予測する
y_test_pred = model.predict(X_test)特徴量の重要度をグラフで表示する(スキップOK)

ランダムフォレストモデルでは特徴量の重要度を求めることができます。

せっかくなら見たいにゃ。
#特徴量の重要度をグラフ表示する
importances = model.feature_importances_
indices = np.argsort(importances)[::-1]
titanic = ["Pclass", "Sex", "Age","SibSp","Parch", "Fare","Embarked"]
names = [titanic[i] for i in indices]
plt.figure()
plt.bar(range(X_train.shape[1]),importances[indices])
plt.xticks(range(X_train.shape[1]),names,rotation=90)
plt.show()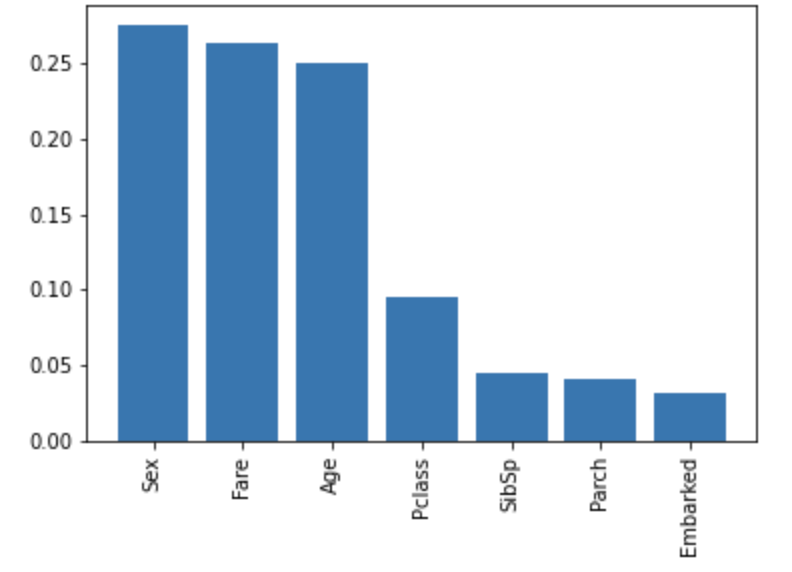
モデルの評価

出来上がった「y_test_pred」を提出してみたところ0.73ほどの正解率でした。

今回はランダムフォレストを用いましたが分類問題と解くのに他にもたくさんの手法があるので色々なモデルを比べてみて精度を確かめるのも面白そうです。
おわりに

今回はランダムフォレストモデルを使ってタイタニック号の生存者予測を行いました。
データサイエンスを楽しんでいただけたら嬉しいです。

他にもいろんな記事があるにゃ。


コメント