初めに
どーも、将棋と筋トレが好きな学生エンジニアのゆうき(@engieerblog_Yu)です。
今回はデータサイエンスに必要な統計編6回目にして、t分布についてまとめていきたいと思います!
前回までの記事です。
t分布の特徴
スチューデント分布と呼ばれるt分布は、自由度nを用いて\(t_n(x)\)と表されます。
t分布は、以下のような形をしています。
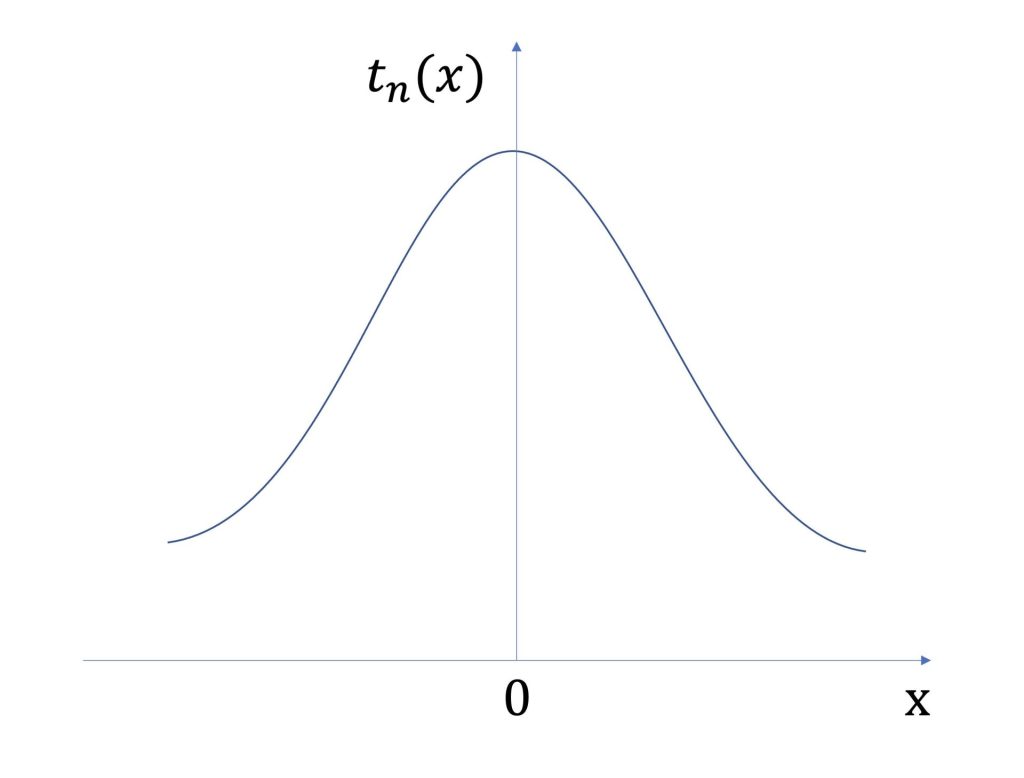
平均が0で左右対称のグラフになっていますね。
t分布の特徴としては、以下のようになります。
標準正規分布と似たような形をしている
標本が少ない場合に用いられる
標準正規分布よりも外れ値の確率が大きい
例えば、日本に住んでいる人の体重の分布は正規分布に従うのに対して、◯◯町に住んでいる人の体重の分布はt分布に従います。
このように標本数が大きい場合は、正規分布に従うのに対して、標本が少ない場合はt分布にを使うのが一般的です。
t分布を使う場合には、標本が少ないため、平均から離れた値が出る確率が高くなります。
よって外れ値の確率が標準正規分布よりも大きくなっている特徴があります。
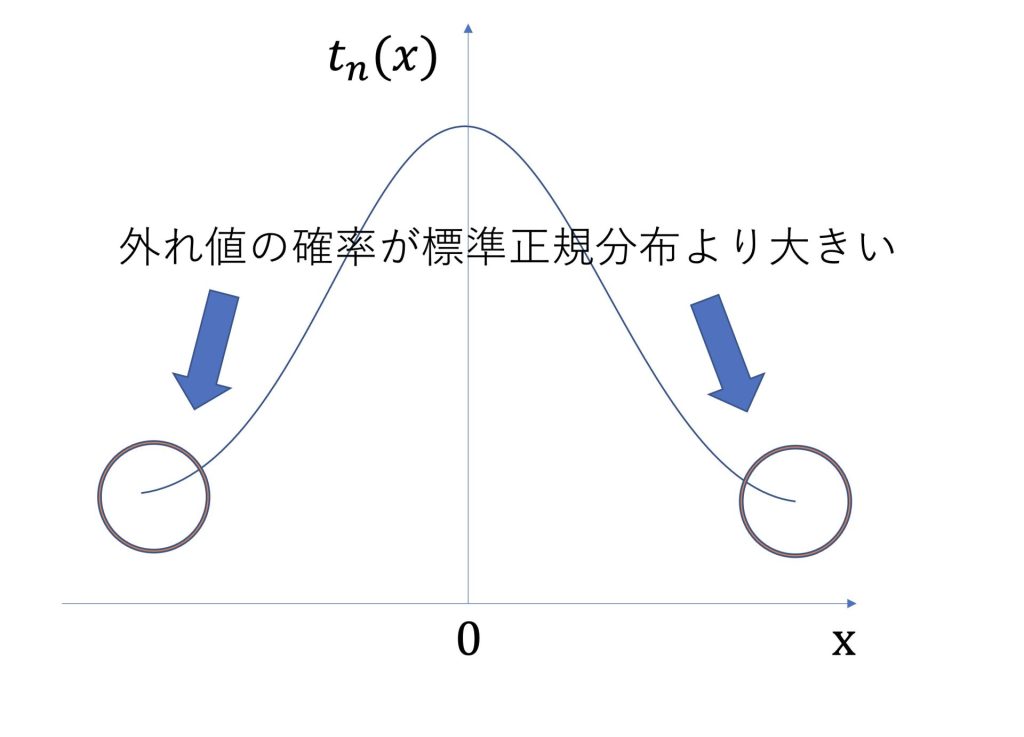
例えば、1億人の体重を調べてみると平均あたりの数が最も多く、100kg以上や30kg以下の人はかなり少なくなるはずです。
しかし10人の体重を調べてみると、たまたま100kg以上の人が二人いたりなどして、分布が平均から離れた値に大きく影響を受けてしまう可能性があります。
よって標本数が少ないt分布では、外れ値の確率密度が大きくなります。
t分布の式
t分布の式にも軽く触れておきたいと思います。
標準正規分布に従う変数をY、自由度nのカイ二乗分布に従う変数をZとする。
\(X=\frac{Y}{\sqrt{\frac{Z}{n}}}\)とおくと、Xは自由度nのt分布に従う。
\(t_n(x)=\frac{1}{\sqrt{n}B(\frac{n}{2},\frac{1}{2})}(\frac{x^2}{n}+1)^{-\frac{n+1}{2}}\)
B(p,q)は以下で定義されます。
\(B(p,q)=\int_0^1x^{p-1}(1-x)^{q-1}dx\)
\(sub.to:p>0,q>0)\)
上記からわかるt分布の性質として、カイ二乗分布の変数の平方根をとるとt分布になるという特徴があります。
まとめ
t分布は標準正規分布と似たような形をしていて、標本が少ない場合に用いられる
t分布は、標準正規分布よりも外れ値の確率が大きい
カイ二乗分布の変数の平方根をとるとt分布になる
今回はデータサイエンスに用いる統計6回目にして、t分布についてまとめました!
6回目まで読んでいただけた人は、データサイエンスで用いる分布を理解することができてきたことと思います!
次回から区間推定や検定に入っていきたいと思います!

最後まで読んでいただきありがとうございました。

他にもいろんな記事があるにゃ。


コメント