目次
はじめに

こんにちは。学生エンジニアのゆうき(@engieerblog_Yu)です。
今回はscikit-learnというデータ分析のライブラリを使って単回帰分析を行っていこうと思います。
今回の記事をお勧めする方は
データ分析に興味がある
scikit-learnを使ってみたい
回帰分析について理解しているか自信がない
に当てはまる人です。
単回帰分析とは?
まずは単回帰分析とは何なんかということについてです。
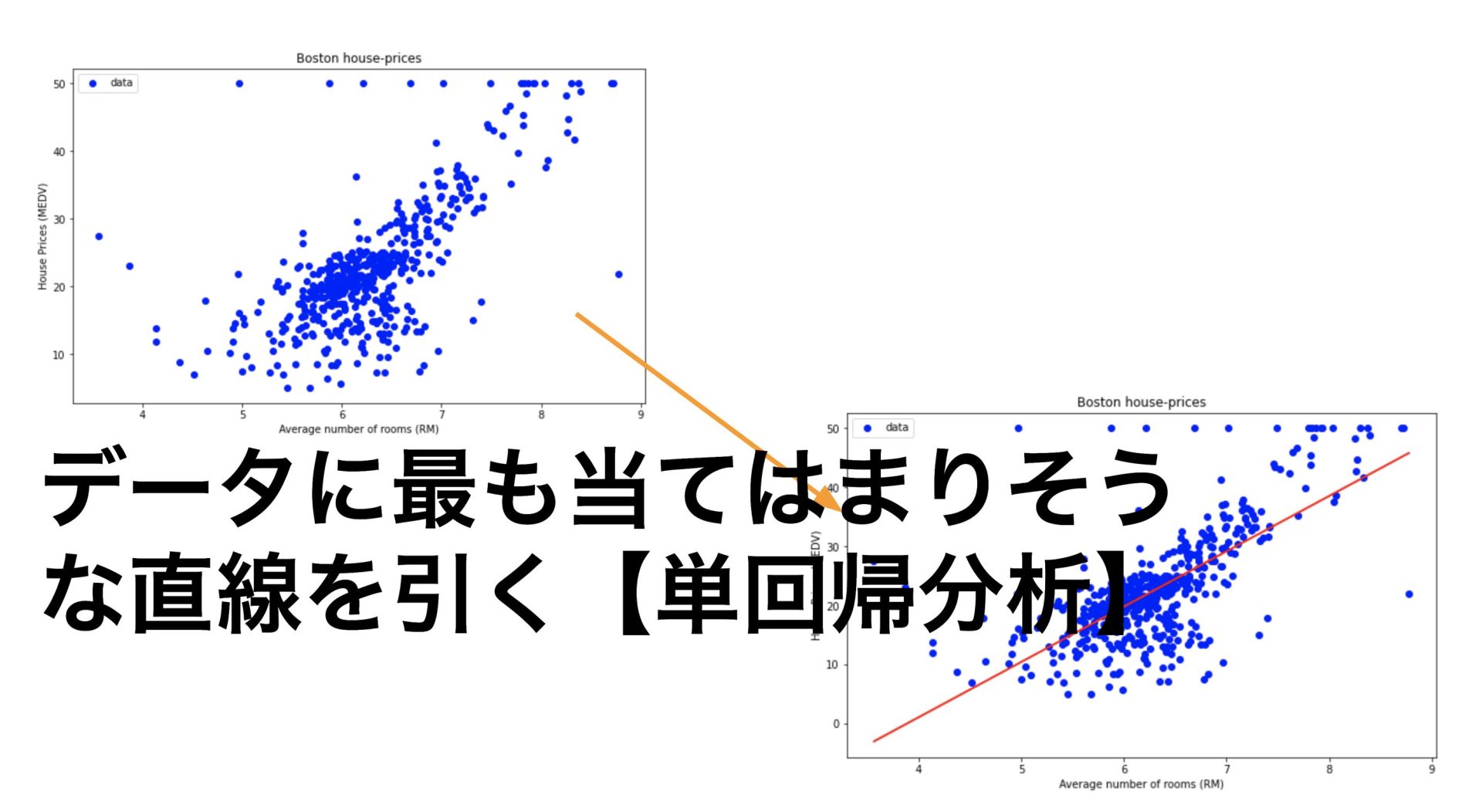
一言で簡単に表そうとするならばデータに最も当てはまりそうな直線をひくということです。
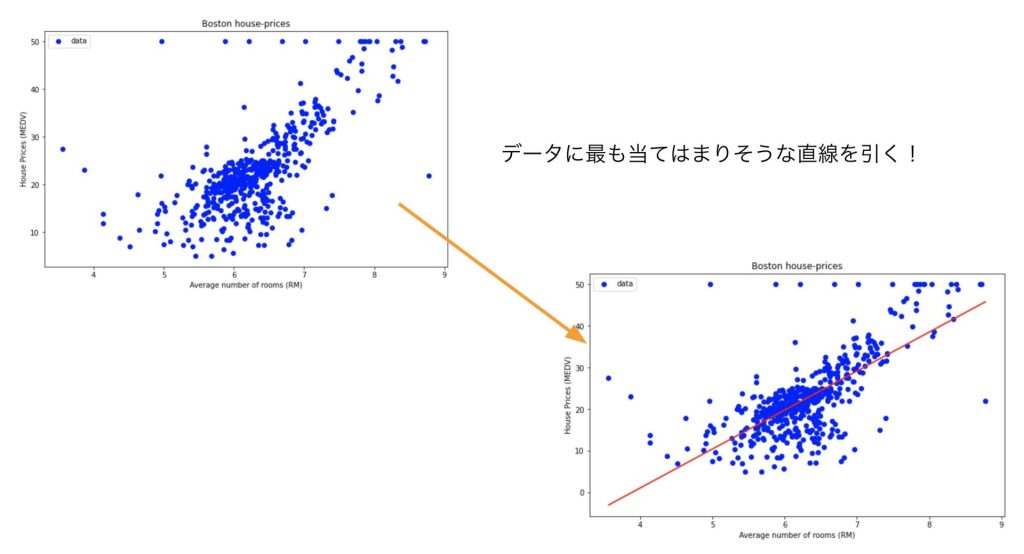
つまり
$$y = ax + b$$
と表される最適なaとbの値を探すということです。
また今回は単回帰分析を行いますが回帰分析にも色々な種類があります。
線形回帰
非線形回帰
の二つです。

何やら難しそうにゃ。
いきなり難しい言葉になったように思えるかもしれませんが線形は直線、非線形は曲線という意味です。
また線形回帰と非線形回帰では以下のように分析の手法が異なります。
線形回帰
・単回帰分析
・重回帰分析
非線形回帰
・多項式分析
今回は線形回帰の単回帰分析についてやっているということを理解していただけたらと思います。
ただし先ほどの単回帰分析についてこんな疑問を持った方もいると思います。

線を引くって言ってもどんな線を引けばいいにゃ?
こう思った方は鋭いです。
最も当てはまる線を引くためには線とデータの誤差を最小にするという操作が必要です。
今回は最小二乗法と言った手法を使って単回帰分析を行っていきます。
最小二乗法について(難しい方は後回しでもOKです)
最小二乗法とは一つ一つのデータのy座標と直線の距離の差(残差)の二乗が最も小さくなるような直線を引くという手法です。

????????。
ごめんなさい。わかりづらいですよね。図で表すと残差とは以下のようなものになります。
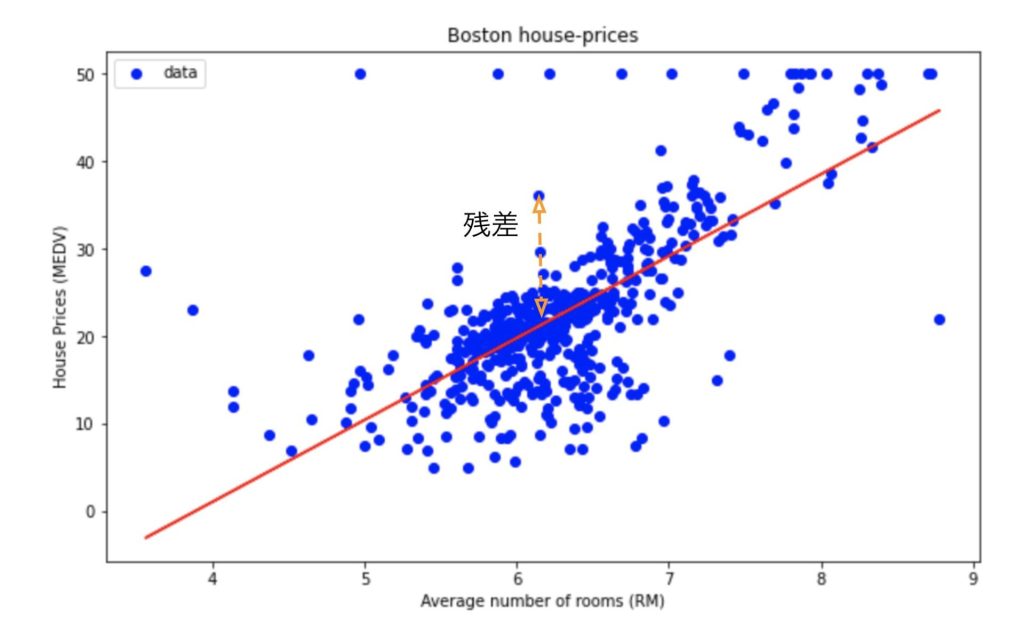
数式は以下のようになります。
$$J=\sum ^{n}_{i=1}(\left( y_{i}-f\left( x_{i}\right) \right) ^{2}$$
平均二乗誤差では各々の点と、直線の誤差の二乗誤差を考えます。
二乗誤差の和である、Jの値が最も小さくなる時に誤差が最も少なくなるということです。
二乗する理由としては直線よりデータのy座標が上か下かは関係なしに距離の差を考えたいからです。

それでは実際に単回帰分析をやっていきましょう!
ライブラリのインポート
今回用いるのは以下のライブラリです。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_errorデータの取得と確認
今回はボストン住宅価格データセットについてデータ分析を行っていこうと思います。
まずは説明変数に関しての説明です。
| カラム | 説明 |
| CRIM | 町ごとの一人当たりの犯罪率 |
| ZN | 宅地の比率が25000平方フィートを超える敷地に区画されている |
| INDUS | 町あたりの非小売業エーカーの割合 |
| CHAS | チャーリーズ川ダミー変数(川の境界にある場合は1,それ以外の場合は0 |
| NOX | 一酸化窒素濃度(1000万分の1) |
| RM | 1住戸あたりの平均部屋数 |
| AGE | 1940年以前に建設された所有専有ユニットの年齢比率 |
| DIS | 5つのボストンの雇用センターまでの加重距離 |
| RAD | ラジアルハイウェイへのアクセス可能性の指標 |
| TAX | 10000ドルあたりの税全額固定資産税率 |
| PTRATIO | 生徒教師の比率 |
| B | 町における黒人の割合 |
| LSTAT | 人口当たり地位が低い率 |
| MEDV | 1000ドルでの所有者居住住宅の中央値 |
今回は単回帰分析ですのでMEDVの値をRMのみを使って予測していきたいと思います。
まずはデータを読み込みます。
df = pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/housing/housing.data',header=None,sep='\s+')
df.columns = ['CRIM','ZN','INDUS','CHAS','NOX','RM','AGE','DIS','RAD','TAX','PTRTIO','B','LSTAT','MEDV']
df.head()しっかりデータが読み込めていることがわかります。
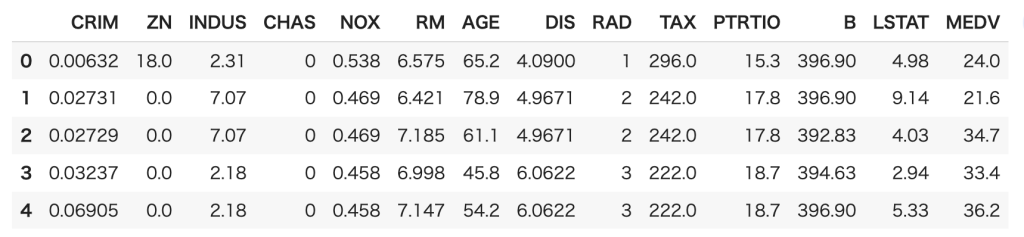
次にデータのサイズを確認します。
506行16列のデータがあることがわかります。

それでは単回帰分析のX(説明変数)、y(目的変数)を代入していきましょう。
X = df[:506][['RM']].values
y = df[:506]['MEDV'].values
しっかり代入できていることがわかります。
訓練データとテストデータの分割

次に訓練データとテストデータの分割を行います。
訓練データとはモデルの訓練に用いるデータです。
テストデータとはモデルの評価に用いるデータです。
慣例的に訓練データ:テストデータの比率は7:3か8:2が良いとされています。
今回は8:2で分割していこうと思います。
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.2,random_state=0)訓練データ:テストデータは7:3か8:3
モデルの訓練

それではモデルの訓練を行っていきましょう。
今回は線形回帰ですのでLInearRegression()を用います。
訓練用データでモデルの訓練を行います。
model = LinearRegression()
model.fit(X_train,y_train)モデルの評価
それでは訓練が完了しましたのでモデルの評価を行っていきます。
訓練用のデータの評価をするためのy_train_predとテストデータの評価をするためのy_test_predをそれぞれ定義します。
y_train_pred = model.predict(X_train)
y_test_pred = model.predict(X_test)どのような回帰分析ができているのか実際にプロットしてみます。
plt.figure(figsize=(10,6))
plt.scatter(X,y,color='b',label='data')
plt.plot(X_train,y_train_pred,color='r',linestyle='-')
plt.xlabel('Average number of rooms (RM)')
plt.ylabel('House Prices (MEDV)')
plt.title('Boston house-prices')
plt.legend()
plt.show()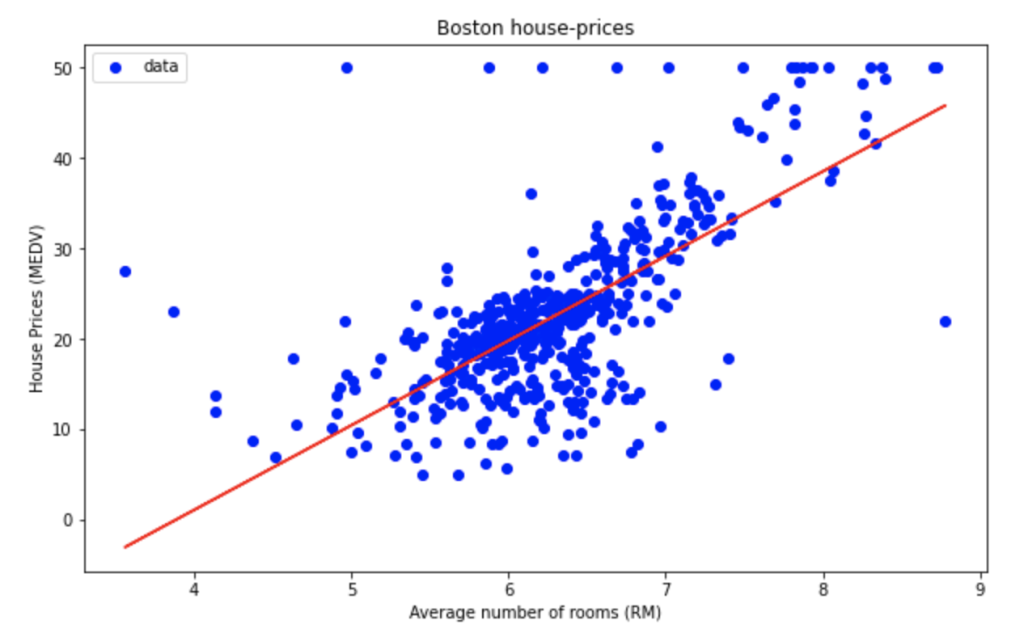
それでは最後に二乗誤差を求めてみます。
訓練用データの誤差とテスト用データの誤差が近い値になっていることがわかります。

おわりに

今回はscikit-learnというデータ分析のライブラリを使って単回帰分析を行っていきました。
scikit-learnはデータ分析の入門的なライブラリですので機械学習の概観を知るという意味でとてもお勧めです。
続きとして重回帰分析についての記事も出しているのでそちらも合わせてどうぞ。

他にもいろんな記事があるにゃ。


コメント