初めに
こんにちは!シミュレーション技法研究室に所属しているゆうき(@engieerblog_Yu)です。
今回はシミュレーションの面白さを伝えたいと思います!
意外とシミュレーションという言葉はわかるけれど、実際何かわからないという方は多いのではないでしょうか?
今回は簡単にシミュレーションとは何かということについて解説していきたいと思います!
熱シミュレーションの例
今回は、簡単な熱シミュレーションを紹介していきたいと思います。
ここに、ある金属板が一つあったとします。
この金属板の左下端を火で炙っていきます。
すると、熱はどうやって金属板を伝わっていくのかについて知りたいとします。
しかし実際に実験するのはとても大変です。
金属板を用意しなければならない
温度を測らなければならない
火で火傷する可能性がある…….etc
など多くのコストがかかります。
この時に使われるのがシミュレーションです。
シミュレーションでは、コンピュータ上で熱が移っていくのかを計算します。
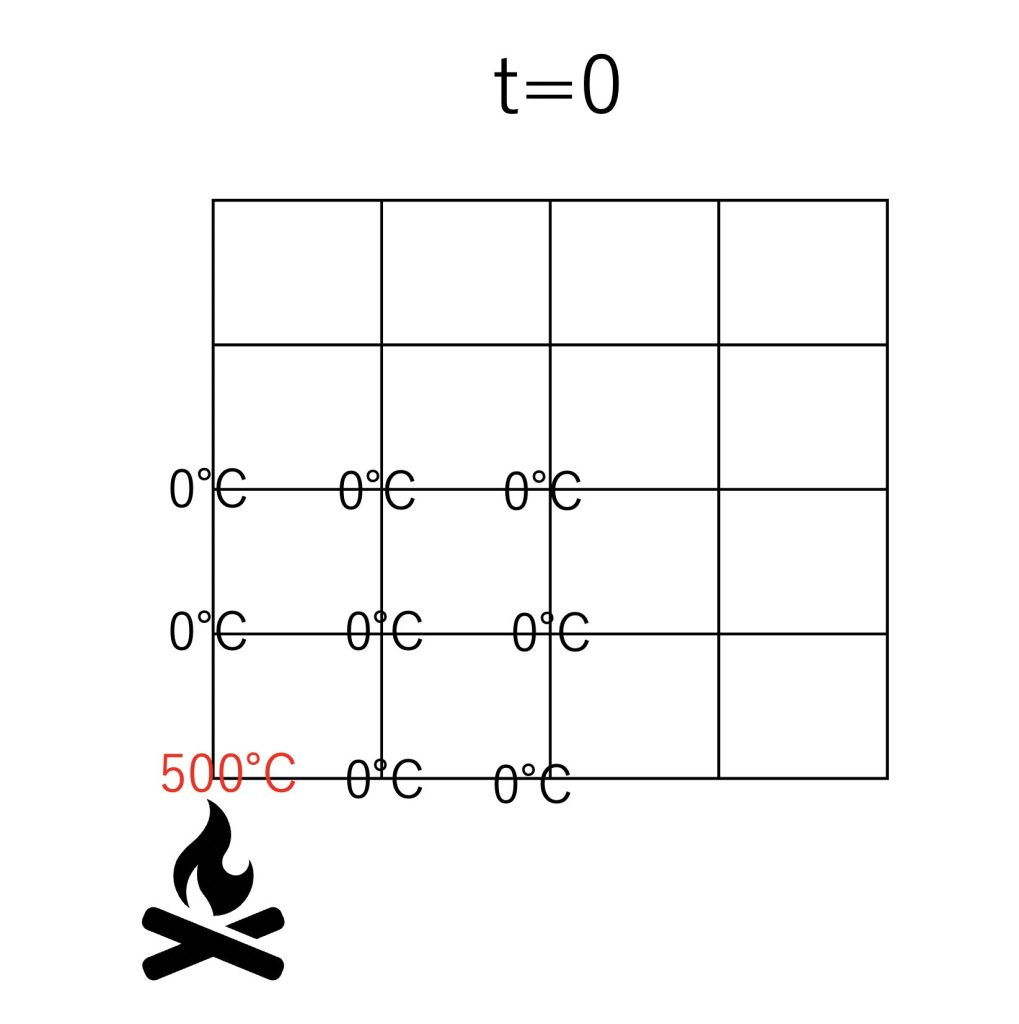
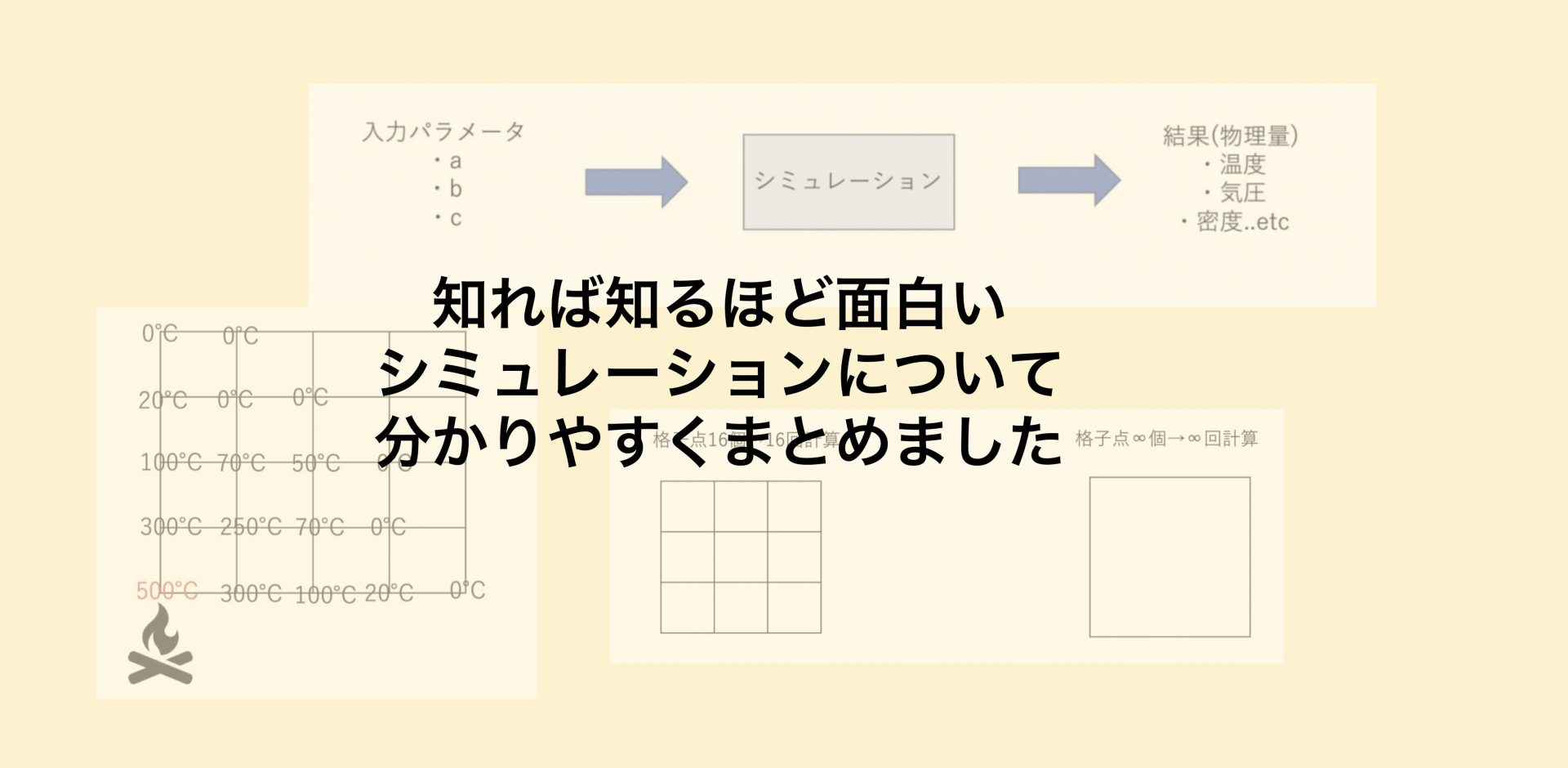
具体的には、以下のように金属板を格子状にしたものを考えます。
以下は時刻が0の初期状態と言われる状態です。
シミュレーションでは格子点ごとに、ある物理量(今回は温度)が計算されます。
次にちょっと時間が経ったときのシミュレーション結果です。
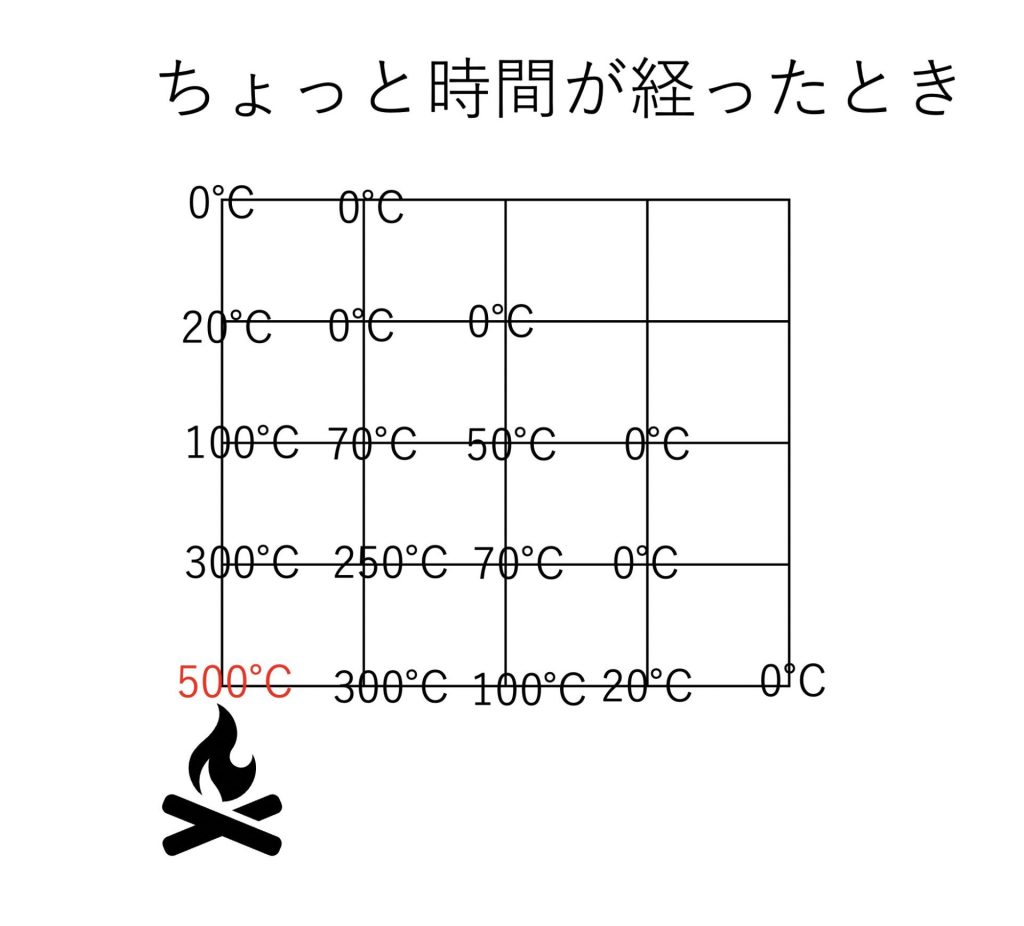
格子点ごとに温度が計算されています。

時間が経つと上記のような熱分布になりました。
なんとなくイメージは湧いたでしょうか?
ここで色々な疑問が生じると思います。
どうやって温度を計算しているの?
なんで格子に区切る必要があるの?
それぞれについて解説していきます。
どうやって温度を計算しているのか?
先ほどの図で説明すると、何やら魔法のようなもので温度が計算されているように思えるかもしれません。
しかし実際にはなんらかの方程式によって、温度が計算されています。
そのようなシミュレーションでの場を支配している方程式のことを支配方程式といいます。
イメージとしては以下のようになります。

入力パラメータとして、金属板の情報を熱の支配方程式に渡すことで温度が計算されます。
ざっくり式で表すと(温度)=F(熱伝導率)ですね。(Fは支配方程式)
入力パラメータと結果は、複数ある場合ももちろんあります。
シミュレーションを一般的に表した図が以下のようなものになります。

(温度,気圧,密度…etc)=F(a,b,c)で表されるという訳です。
どうして格子に区切る必要があるのか?
格子に区切る理由は主に以下です。
コンピュータのメモリが有限だから
先ほど説明した物理量の計算は格子点ごとに行われます。
つまり格子点の数だけ計算する必要があるということです。
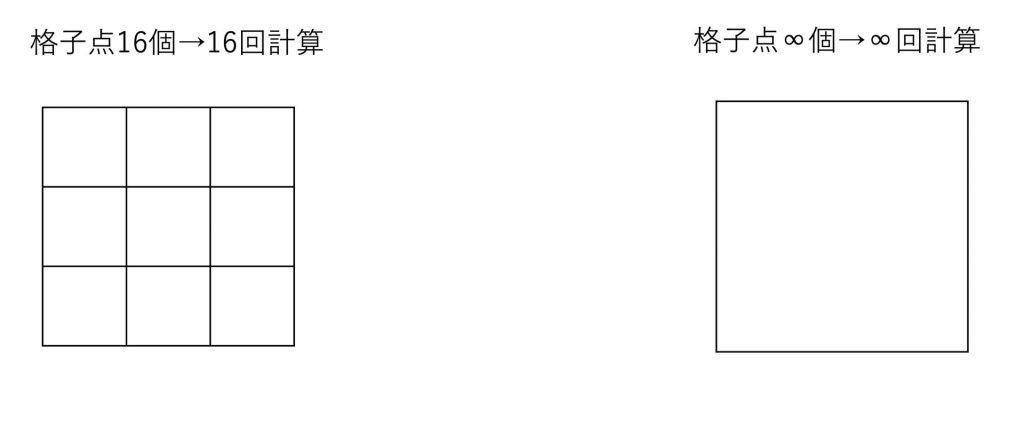
現実世界のような連続した場(格子点が無い状態)を考えるためには、∞個の格子点を考える必要があります。
これはメモリが有限なコンピュータは処理することができません。
よって近似的に格子点に区切って解像度を落とすことで、計算できるようにするのが一般的です。
シミュレーションの問題点
何やら万能そうに思えるシミュレーションにも問題点があります。
大規模なシミュレーションになると膨大な実行時間がかかってしまう
ということです。
先ほどは二次元のデータを考えていましたが、三次元、四次元(三次元に時間を考慮したデータ)にすると計算量が指数関数的に爆発します。
一回のシミュレーションの実行に100h以上かかってしまうこともザラにあります。
私はシミュレーションを機械学習で代替することで、実行時間を短縮しちゃおうというような研究をしているので興味があればそちらも併せてどうぞ。
終わりに
今回はシミュレーションについて簡単に解説してみました!
シミュレーションについてなんとなく興味を持っていただけたら嬉しいです。

最後まで読んでいただきありがとうございました。
他にも研究関係の記事を書いているのでそちらも併せてどうぞ。





コメント