目次
はじめに
こんにちは。将棋と筋トレが好きな、情報系大学生のゆうき(@engieerblog_Yu)です。
今回はニューラルネットワークの勾配の計算に用いられる、誤差逆伝播法のAffineレイヤ・Softmaxレイヤについてまとめていきたいと思います。
誤差逆伝播法について
前回までの記事で勾配降下法を紹介しました。
勾配降下法は損失関数の値が小さくなる方向の勾配に、解を降下させていくといったものでした。
勾配を計算する方法は二つあり、数値微分と誤差逆伝播法です。
数値微分を用いると正確である反面、パラメータが大量になった場合、計算に時間がかかってしまうというデメリットがあります。
そこで使われるのが誤差逆伝播法で、実装が複雑という欠点はありますが、計算が早いので数値微分の代わりに用いられることがほとんどです。
誤差逆伝播法で実装し、数値微分で実装があっているか確認するという流れがどうやら主流であるようです。
誤差逆伝播法で用いられる計算グラフや逆伝播の法則については、前回までの記事で解説しているので合わせてどうぞ。
逆伝搬の法則
逆伝搬の法則については以下の図のようになります。
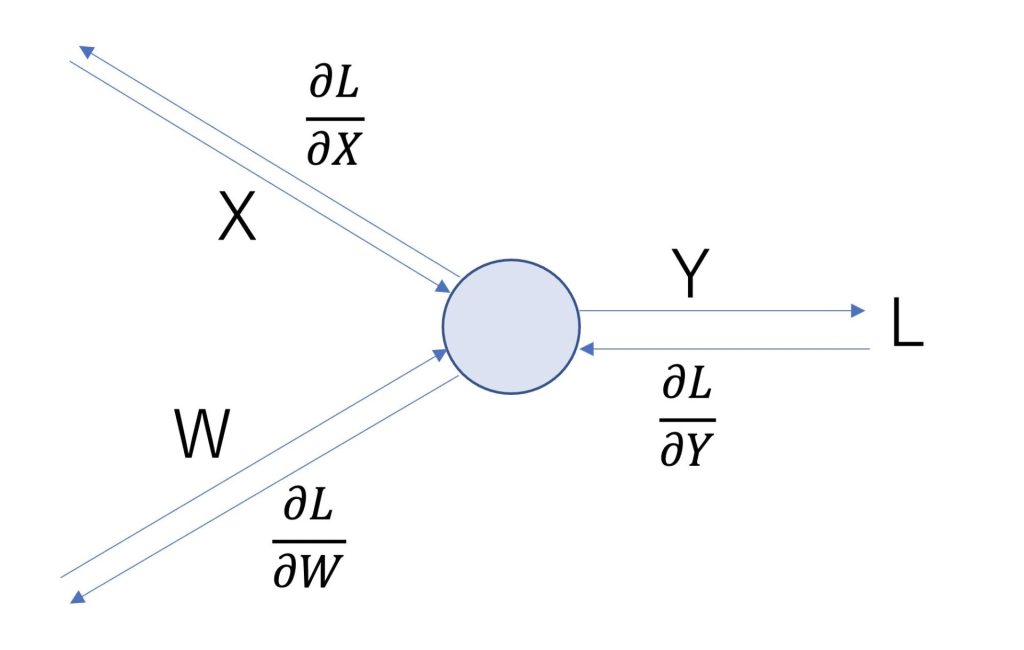
レイヤの種類に関わらず、一つ前の偏微分に偏微分をかけることで計算できます。
レイヤに何を使うかによって偏微分の値が変化します。
Affineレイヤ
Affineレイヤは入力が行列である時の、ドット積を計算する際に用いられます。
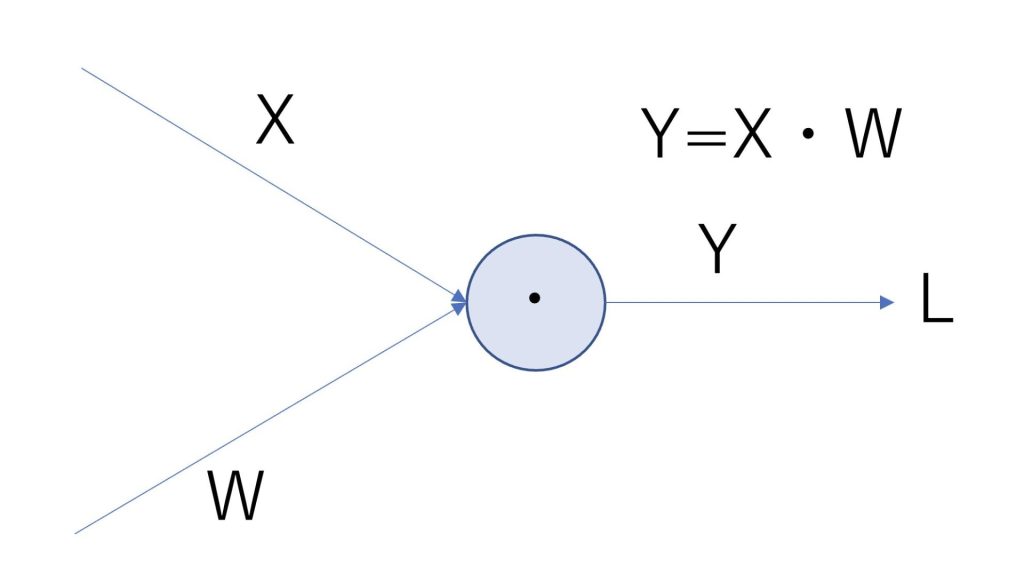
逆伝搬はドット積の場合も以下のようになります。
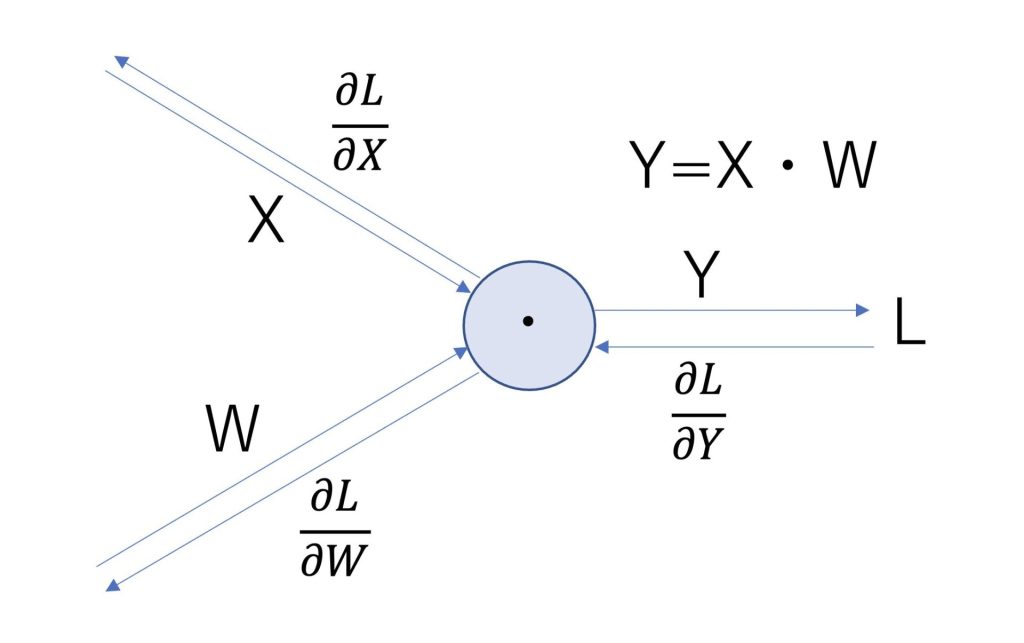
計算すると、偏微分は以下のようになります。
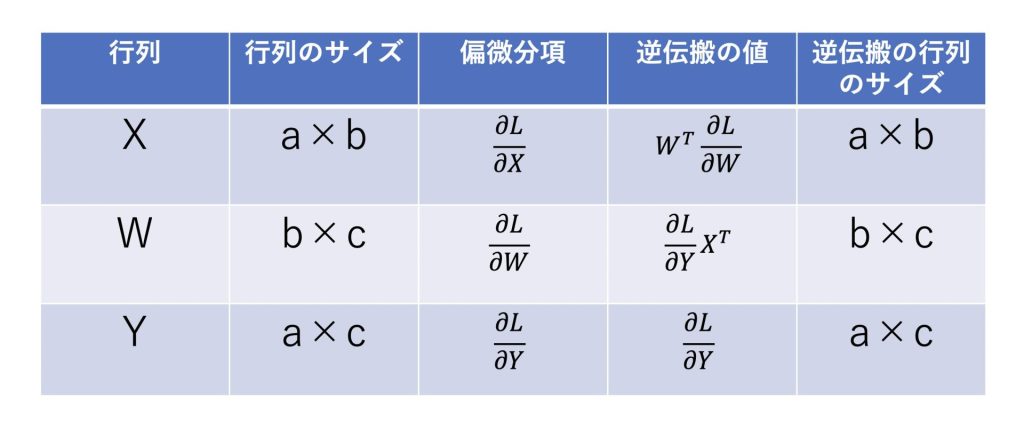
\(\frac{∂L}{∂X}=\frac{∂L}{∂Y}W^T\)
\(\frac{∂L}{∂W}=X^T\frac{∂L}{∂Y}\)
また行列の掛け算は行と列が一致している必要があります。
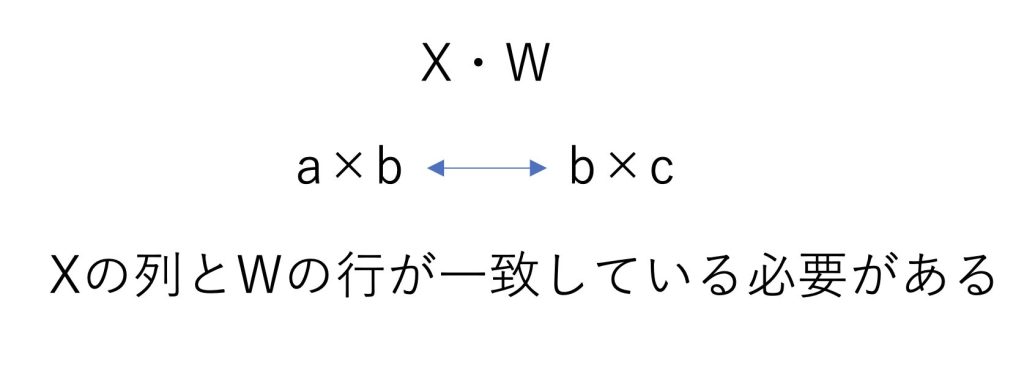
よって表でまとめると、行列サイズは以下の条件を満たしていないと掛け算をすることができません。
AffineレイヤをPythonで実装
それでは上記のAffineレイヤをPythonで実装してみます。
重み行列だけでなくバイアスも考慮しています。
class Affine:
def __init__(self,W,b):
self.W = W
self.b = b
self.x = None
self.dW = None
self.db = None
def forward(self,x):
self.x = x
out = np.dot(x,self.W) + self.b
return out
def backward(self,dout):
dx = np.dot(dout,self.W.T)
self.dW = np.dot(self.x.T,dout)
self.db = np.sum(dout,axis=0)
return dx適当な値を設定します。
W = np.array([[1,2,3],[1,4,6]])
b = 2
X = np.array([[2,4],[2,1],[4,3]])
affine = Affine(W,b)
Y = affine.forward(X)
print(Y)
dx = affine.backward(1)
print(dx)行列Yと\(\frac{∂L}{∂x}\)の値が出力できました。
[[ 8 22 32]
[ 5 10 14]
[ 9 22 32]]
[[1 1]
[2 4]
[3 6]]Softmaxレイヤ
Softmaxレイヤは、出力層に用いられます。
Softmaxレイヤは、分類問題でのそれぞれのスコアを正規化して出力します。
ハムスター、カンガルー、馬の画像のどれかひとつが与えられて、その画像がどれであるか分類したいとします。
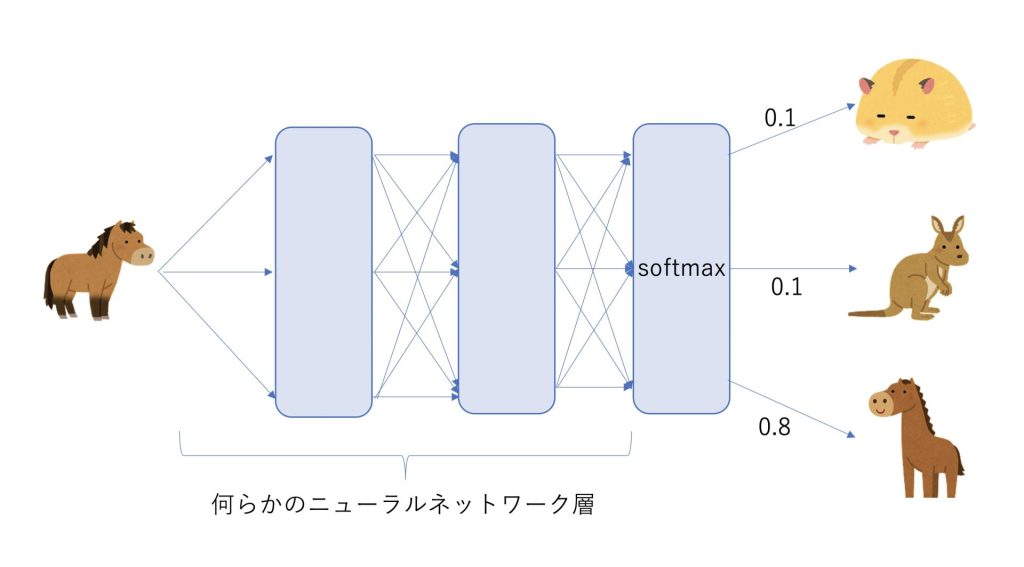
ニューラルネットワーク層を通して出てきた値が、[0.1,0.1,0.8]という値であった場合、それぞれが確率に相当します。
ハムスターの確率が10%、カンガルーの確率が10%、馬の確率が80%になります。
今回の正解は馬なので、訓練誤差が最も小さくなるのは[0,0,1]となる場合となります。
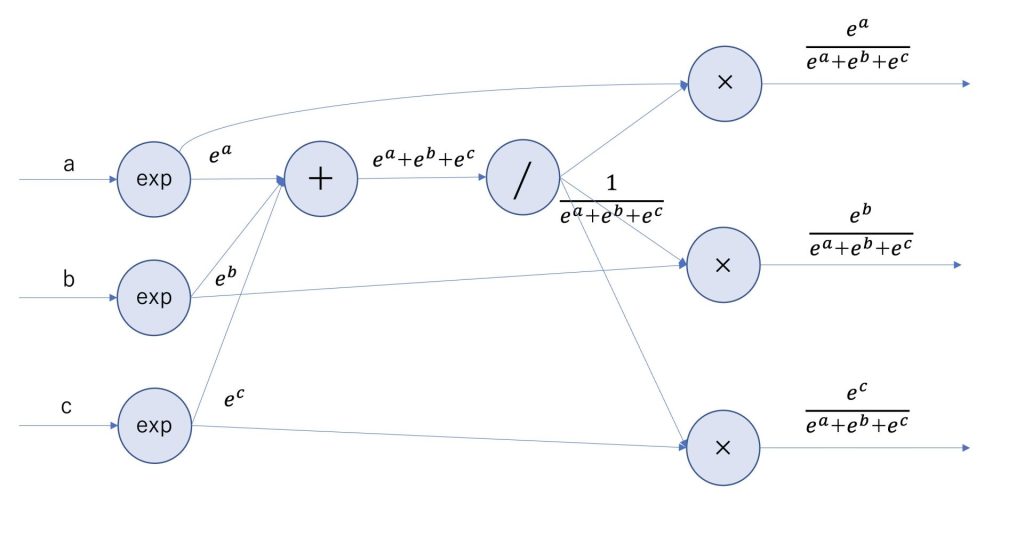
Softmaxレイヤは以下で定義されます。
\(y_k=\frac{e^x}{\sum_{i=1}^{n}e^x}\)
Softmaxレイヤはaとbとcの3入力の場合、以下のような計算グラフになります。
Softmax-with-lossレイヤ
分類問題の誤差を計算するために、交差エントロピー誤差が用いられます。
交差エントロピー誤差は以下で計算されます。
\(E=-\sum_{k}t_klogy_k\)
先ほどの動物の分類問題の例で交差エントロピー誤差を計算してみます。
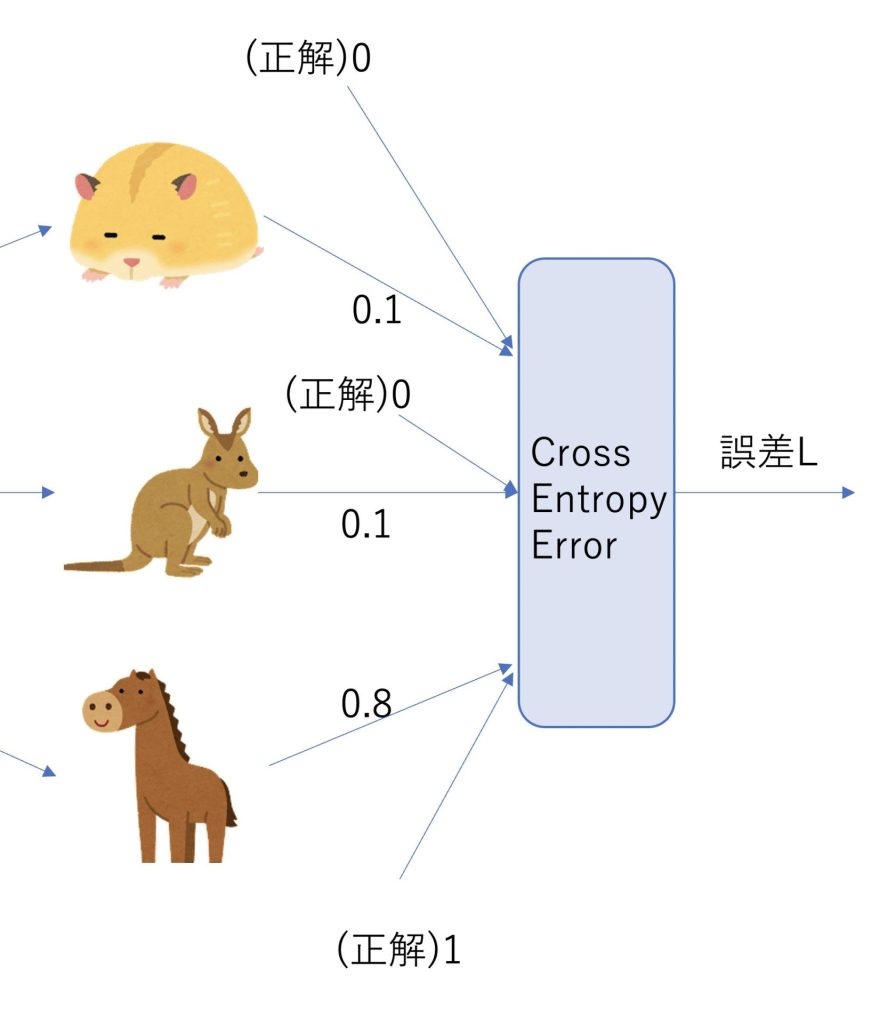
誤差LをPythonで計算してみましょう。
def cross_entropy(y,t):
delta = 1e-10
return -np.sum(t * np.log(y + delta))import numpy as np
y = np.array([0.1,0.1,0.8])
t = np.array([0,0,1])
print(cross_entropy(np.array(y),np.array(t)))交差エントロピー誤差は以下のようになりました。
0.2231435511892097交差エントロピー誤差は、正解と予測の値が遠いと急激に大きくなる傾向があります。
誤差逆伝播法におけるSoftmaxレイヤの有用性について
Softmaxレイヤを逆伝播すると、\(y_k-t_k\)の値が返ります。
\(y_k-t_k\)は偏微分項を計算することで導くことができます。
今回は[0-0.1,0-0.1,1-0.8]=[-0.1,-0.1,0.2]となります。
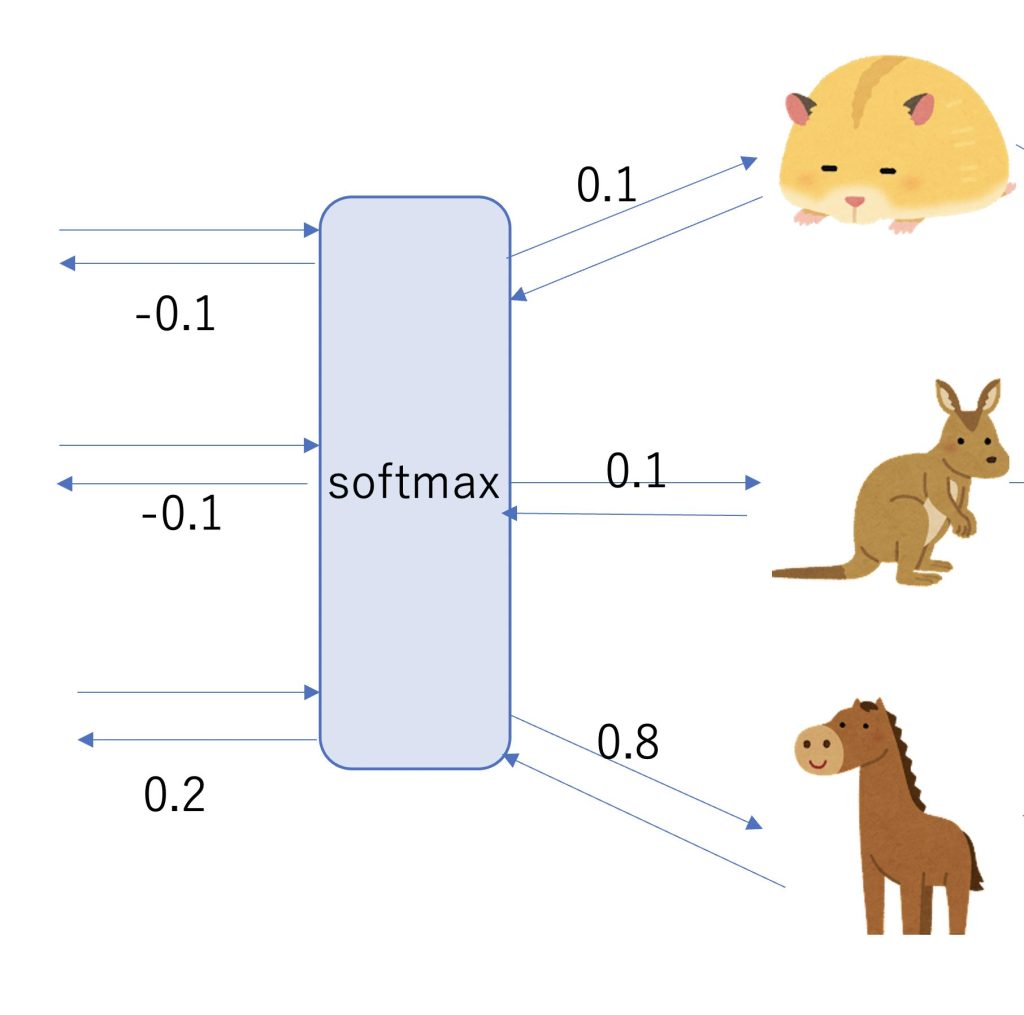
正解と予測の差が大きいほど、逆伝播の値が大きくなります。
逆伝播の値が大きければ大きいほど、誤差が大きく、ニューラルネットワークの学習を大きく進ませることができます。
つまりSoftmaxレイヤを用いると、誤差に応じて、ニューラルネットワークの学習を進ませることができるのです。
まとめ
誤差逆伝播法で実装し、数値微分で実装があっているか確認するという流れが主流
Affineレイヤは行列のドット積を表すことができる
Softmaxレイヤを用いると、誤差に応じてニューラルネットワークの学習を進ませることができる
今回はニューラルネットワークの誤差逆伝播法に用いられるAffineレイヤ・Softmaxレイヤについてまとめました。
機械学習、ディープラーニングを学びたい方におすすめの入門書籍です。
ディープラーニングの理論が分かりやすくまとめられていて、力が身につけたい方におすすめです。

最後まで読んでいただきありがとうございました。

他にもいろんな投稿があるにゃ。





コメント