はじめに
どーも、情報系大学生のゆうき(@engieerblog_Yu)です。
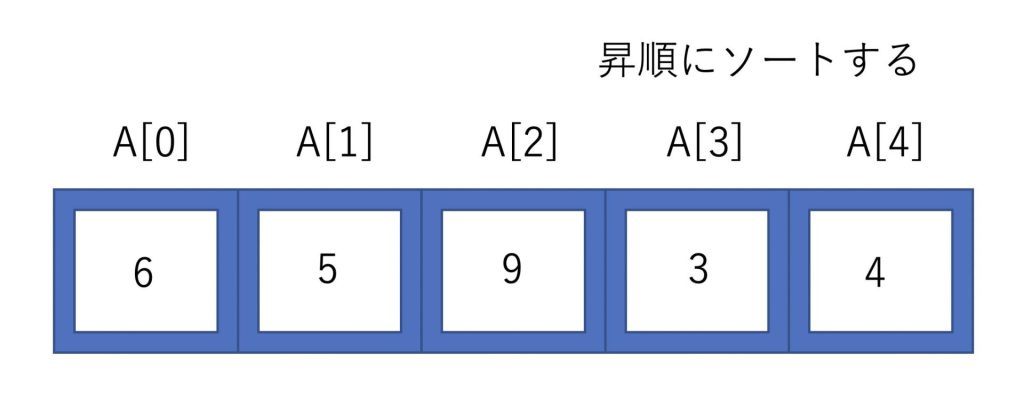
今回はこのような配列を昇順(小さい順)に並び替えていくことを考えましょう。
みなさんはどのように整列しようと考えるでしょうか?
整列の方法はいろいろありますが、計算量の観点でどのような整列アルゴリズムを選ぶかが大切になってきます。
今回はその中のクイックソート、マージソートをまとめていきたいと思います。
前回紹介した整列アルゴリズムよりも計算量が小さく、より良いものになっていて実際にプログラミングのライブラリ関数に採用されているアルゴリズムです。
計算量のオーダー記法について怪しい方はこちらの記事も併せてどうぞ。
クイックソート
まずはクイックソートについてです。
クイックソートのアルゴリズムはこのようになります。
1.配列のどこか一つをpivotに選ぶ。
(pivotの選び方で計算量が変化します。)
2.次にピボット以外のデータをピボットの値より小さいものと大きいデータに分割する。
3.二つに分けられたデータに対してそれぞれ、同じやり方で繰り返し整列を行う。
それではやっていきます。

pivotに選んだ数よりも小さい数を左に、大きい数を右に分けます。
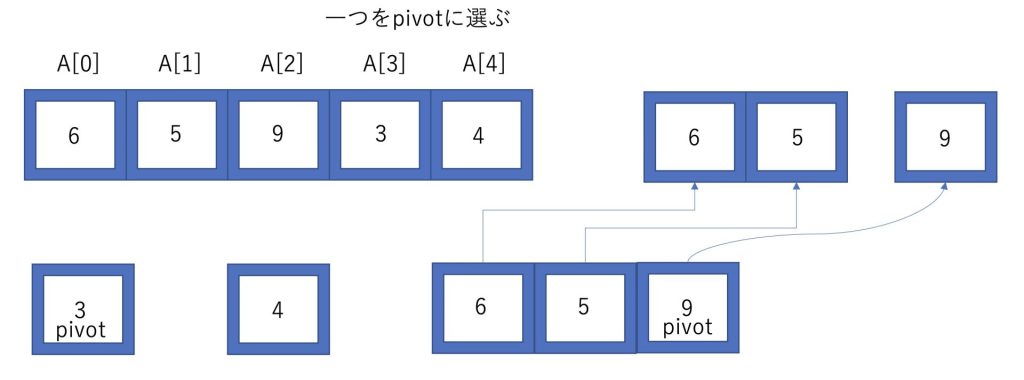
次に右と左に分けた配列に対して、もう一度pivotを選んでいきます。
今回は左に分けた部分は一つなのでそのままです。
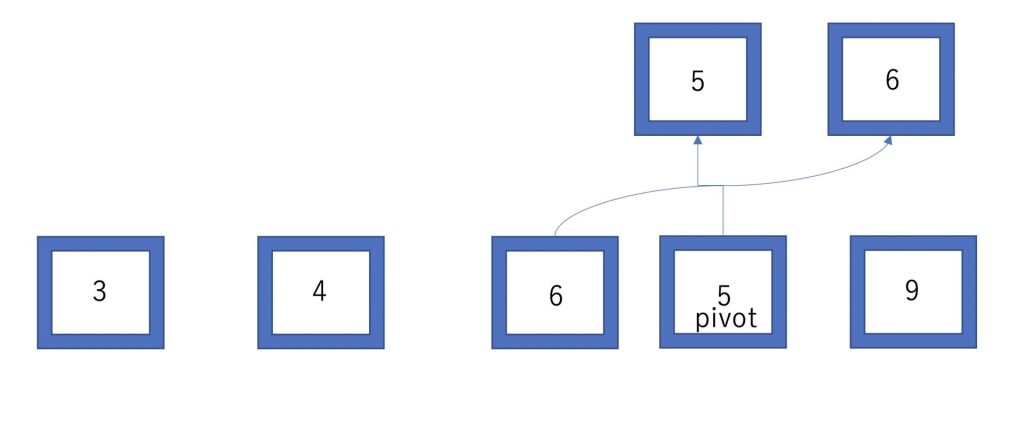
左に分けた配列部分でもう一度pivotを選び、分割します。
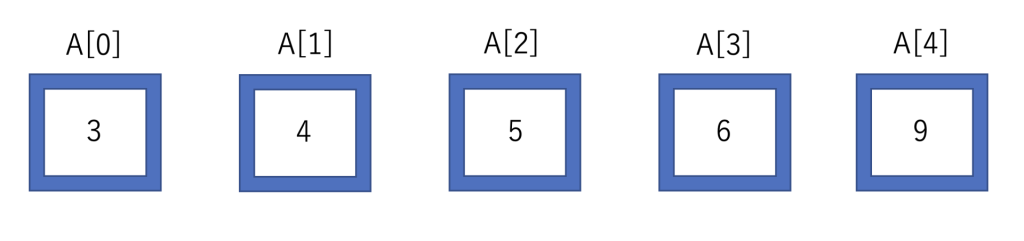
最後に、分割した順に並べると昇順に並び替えることができています。

計算量はこのようになります。
クイックソートの平均計算量はO(nlogn)、最悪計算量はO(n^2)
pivotの選び方によって計算量が変化する
マージソート
次にマージソートについてです。
マージソートのアルゴリズムは主に以下のようになります。
1.配列を一つになるまで分割する
2.2個ずつ昇順になるように統合していく
3.2の処理を元の配列の大きさになるまで繰り返す
まず昇順に並び替えたいデータを一つに分割します。
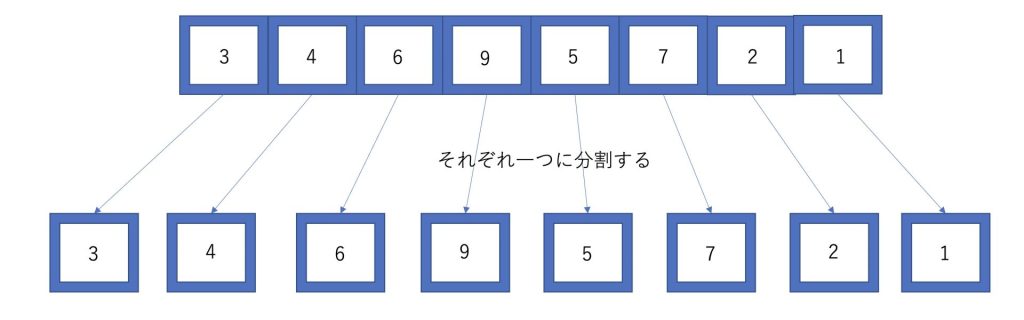
次に分割したデータを二つずつ統合していきます。
統合する際にデータが昇順になるように並び替えます。
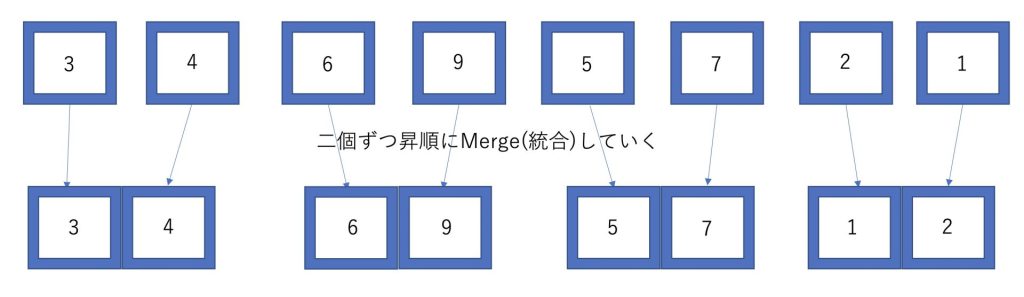
次に、二個ずつまとめて四個ずつ昇順になるように並び替えていきます。
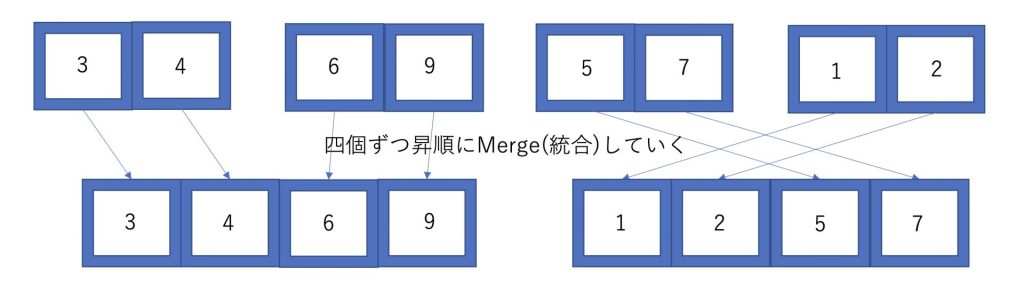
最後に4個の配列が二つできたので、昇順になるように統合していきます。
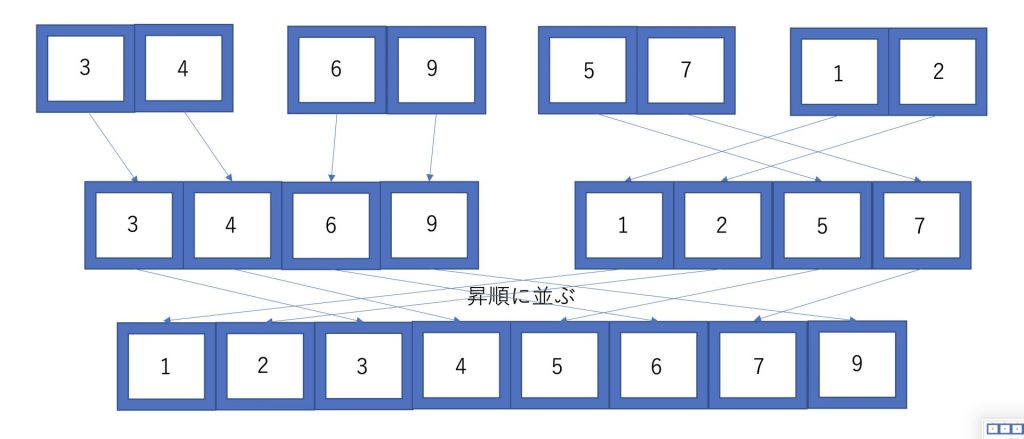
昇順に並べることができました。

計算量はこのようになります。
マージソートは平均計算量O(nlogn)、最悪計算量O(nlogn)
クイックソートよりも最悪計算量が小さい
クイックソートとマージソートはどちらが優れたアルゴリズムか?
クイックソートとマージソートの計算量を比べると、マージソートの方が最悪計算量が小さいため一見マージソートの方が優れているように思えます。
しかしマージソートを行うためには、配列のサイズと同じような作業用配列を用意する必要や、データのコピーを行わなければなりません。
よって計算量が小さくても、一概にどちらが良いと言い切ることが難しくなっています。
まとめ
クイックソートの平均計算量はO(nlogn)、最悪計算量はO(n^2)
クイックソートはpivotの選び方で計算量がかなり変わる
マージソートの平均計算量はO(nlogn)、最悪計算量O(nlogn)
整列の計算量はO(nlogn)よりも良くすることが出来ないということが証明されています。
よって今回紹介したアルゴリズムは、
極めて優良なアルゴリズムであるということが言えます。
アルゴリズムの勉強におすすめの書籍です。

最後まで読んでいただきありがとうございました。

他にもいろんな投稿があるにゃ。





コメント