
こんにちは!ゆーきです!

今回は数学で最も美しいと言われているオイラーの公式について導出と一緒に紹介していきたいと思います!
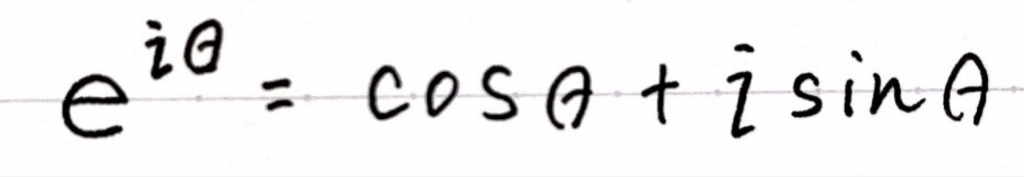

こちらがオイラーの公式になります。
オイラーの公式の凄いところは
指数関数と三角関数と虚数単位iという扱いづらい3つのものがシンプルに一つの等式で表されているということです。

虚数の導入がオイラーの公式のおかげで簡単になったんですね。

理系ならば美しいとは言わないまでも凄い公式だとわかりますよね。

それではオイラーの公式を簡単に導出していきたいと思います!

使うのはマクローリン展開だけです。
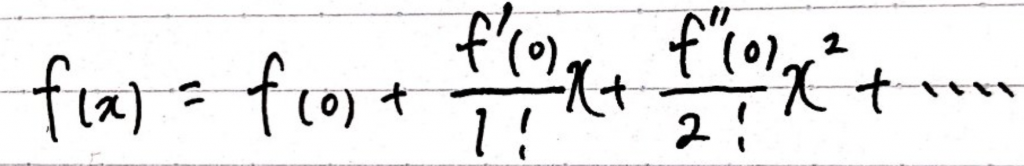
なおマクローリン展開が使えるのはf(x)が何回でも微分可能であり、ラグランジュの剰余項が収束する場合のみです。

ラグランジュの剰余項ってなんだっ?て思ったと思います。とりあえず最後に説明しますね。
今回はcos(θ)とsin(θ)とe^(iθ)についてマクローリン展開を行います。今回はすべての関数がマクローリン展開を使える条件を満たしています。
オイラーの公式の導出

cosθのマクローリン展開はこちらです。
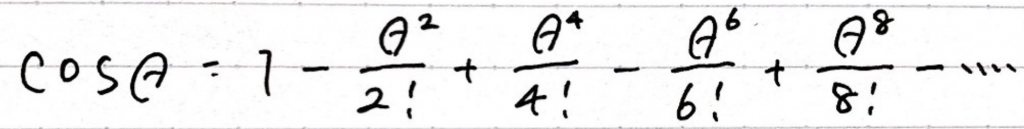

次にsinθのマクローリン展開です。
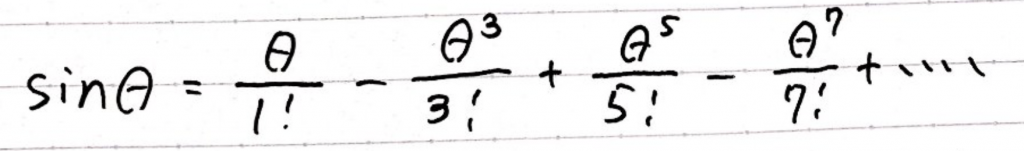

最後にe^iθのマクローリン展開です。
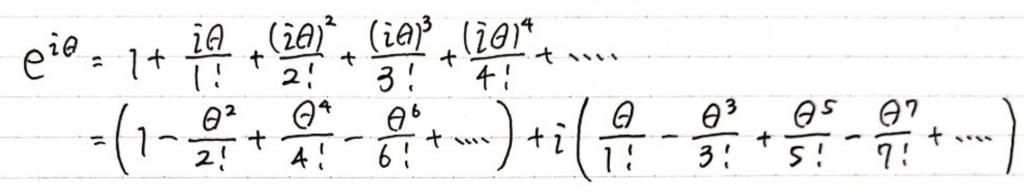

前半のかっこ部分がcosθに一致し、後半のかっこ部分がsinθに一致します。
よってe^iθ=cosθ+isinθが成立します。(証明終)
【補足】ラグランジュの剰余項とダランベールの判定法について
簡単に言うとラグランジュの剰余項とはマクローリン展開の余りです。
その余りであるラグランジュの剰余項がnを無限に飛ばした時に収束するならマクローリン展開の式が成立します。
そのラグランジュの剰余項が収束するか調べるのがダランベールの判定法です。

詳しくはこちらの記事をどうぞ。
今回はすべて収束するのでマクローリン展開が使えます。
オイラーの公式の使われている場面
実際には
・複素関数の極形式をシンプルに表すことができる
・二階線形微分方程式などから虚数を取り除ける
・解析学の解をシンプルに表すことができる

応用範囲がデカすぎますね。

モデル化する際に解をシンプルに表すことができるという点で偉大な公式だと言えます。

大学数学を真剣に勉強している方は少ないので少しでも興味を持っていただけたら幸いです。

最後まで読んでいただきありがとうございました!






コメント