【機械学習】重回帰分析でより良くボストン住宅価格を予測してみよう(初心者向け)

Tweet

はじめに

どーも、学生エンジニアのゆうき(@engineerblog_Yu)です。

今回はscikit-learnで提供されているボストン住宅価格データセットについて重回帰分析を行っていこうと思います。

今回の記事をお勧めする方は

に当てはまる人です。

今回の記事は以下の記事の続きとなっています。

【データサイエンス】単回帰分析で住宅価格を予測してみる【scikit-learn最初の一歩】

学生エンジニアのゆうき( @engieerblog_Yu )です。 今回はscikit-learnというデータ分析のライブラリを使って単回帰分析を行っていこうと思います。 Pythonを用いたデータ分析の入門にはscikit-learnがお勧めです。データ分析に興味がある方は必見です。

prog-you.com

2022.04.19

重回帰分析について

今回は重回帰分析を行いますが、回帰分析にも色々な種類があります。

の二つです。

ねこすけ

これは単回帰分析で勉強したにゃ。

重回帰分析は線形回帰にあたります。

ゆうき

ここから具体的に単回帰分析との違いを説明します。

重回帰分析とは単回帰分析とは異なり、説明変数が2個以上あるものです。

つまり

$$y=ax_{1}+bx_{2}+cx_{3}\ldots$$

と表すことができます。

基本的に単回帰分析と考え方は同じで、最小二乗法などで誤差を最小にするということも同じです。

一つだけ単回帰分析と異なる点は、説明変数が3つ以上になると空間座標でも視覚化することができないという点です。

単回帰分析の場合では以下のようにグラフを書くことができましたが四次元以上になるとグラフを書くことができません。

ゆうき

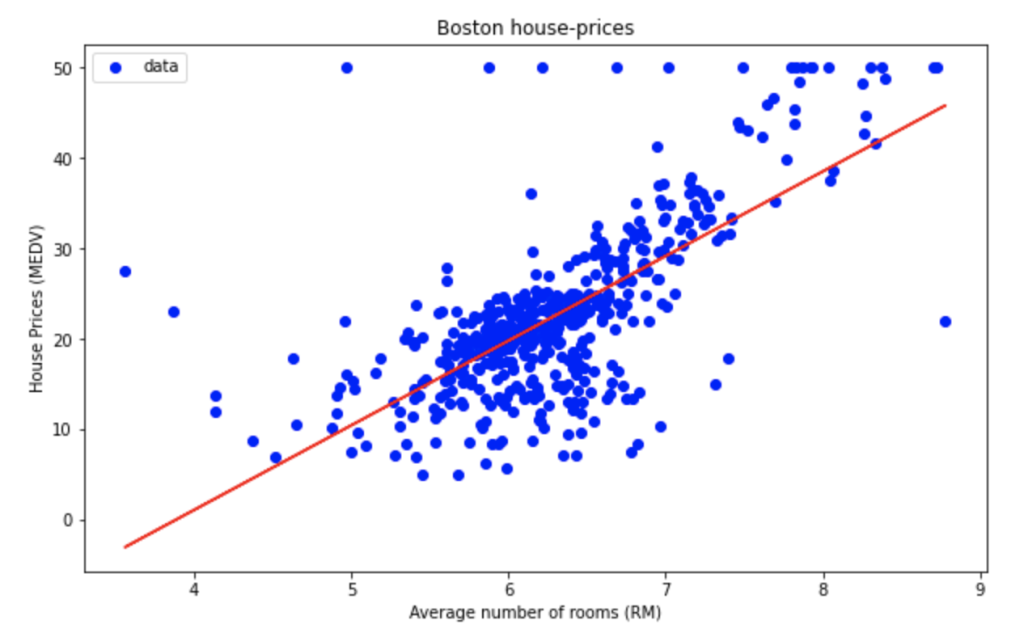
よって直感的に理解することが難しいのです。

ねこすけ

目で見れないなんて不便にゃ。

ゆうき

でもやってることは単回帰分析と同じですので安心してください。

ゆうき

それでは実際に重回帰分析をやっていきましょう！

データセットの確認

今回使うボストンのデータはこのようになっています。(データ数は506件)

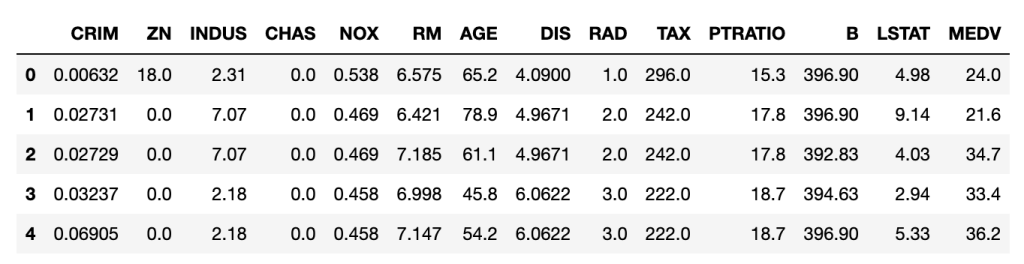
次にそれぞれのデータが何を意味するかについてです。

今回は住宅価格に該当するMEDVの値をscikit-learnを使って予測し、どれくらいの精度なのか確かめていこうと思います。

データの取得

それではまずはデータの方を取得していきましょう。

以下のコードでsklearnの中にあるload_bostonというデータセットを読み込むことができます。

# データセットの取得

from sklearn.datasets import load_boston

dataset = load_boston()

# MEDV以外のデータ
x = dataset.data

# MEDV
t = dataset.target

またdataset.dataはMEDV以外のデータを指し、dataset.targetはMEDVを指しています。

再度今回使用するデータを表示します。

上記のコードではxにMEDV以外のデータ、tにMEDVのデータを代入しています。

データセットの分割

次にデータセットの分割を行っていきます。

# データセットを分割する関数の読み込み
from sklearn.model_selection import train_test_split

# 訓練用データセットとテスト用データセットへの分割
x_train, x_test, t_train, t_test = train_test_split(x, t, test_size=0.3, random_state=0)

train_test_splitについての説明です。

test_size=0.3と指定すると全データ中の30%がテストデータとなります。

またrandom_state=0とすることで実行するたびの分割を同じようにすることができます。(デフォルトでは実行するたびにランダムに分割されます)

重回帰分析をするためのモデルの定義

次にモデルの定義を行っていきます。

from sklearn.linear_model import LinearRegression

# モデルの定義
reg_model = LinearRegression()

今回は線形回帰ですのでLinearRegressionを使います。

標準化

標準化に関する説明です。

データセットのばらつきが大きいときは特に、モデルを訓練させる前に標準化を行います。

標準化とはデータを平均0、分散1に統一するということです。

なぜ標準化が必要なのか気になる方も多いと思います。

例えば車の値段を重回帰分析を使って予測したいとします。

説明変数として耐久年数と車体重量があったとするとそれぞれの単位は(年)と(kg)です。

するとデータのばらつきがkgの方がもちろん大きくなり、平均も大きいので標準化を行わずに訓練すると精度が悪くなる場合があります。

今回もデータの標準化を行うために以下のコードを実行します。

# 標準化を行う
from sklearn.preprocessing import StandardScaler

scaler = StandardScaler()

scaler.fit(x_train)

x_train_scaled = scaler.transform(x_train)
x_test_scaled  = scaler.transform(x_test)

モデルの訓練

それでは訓練用データセットを用いてモデルをより良いものに訓練させていきましょう。

# モデルの訓練
reg_model.fit(x_train_scaled, t_train)

この1行でモデルの訓練は完了です。

精度の検証

最後に精度を検証していきます。

以下のコードで精度を検証していきます。

# 精度の検証（訓練データ）
reg_model.score(x_train_scaled, t_train)

Out[15]:0.7645451026942549

# 精度の検証（テストデータ）
reg_model.score(x_test_scaled, t_test)

Out[16]:0.6733825506400195

スコアとして得られる数は決定係数の値です。

決定係数とは0から1の値をとり、１に近い値であればあるほどモデルの精度が良いものになっているといえます。

訓練データよりもテストデータの方が精度が低くなるのは当たり前なので前処理やモデルを改善することでどれだけ精度を高くしていけるかということが大切になってきます。

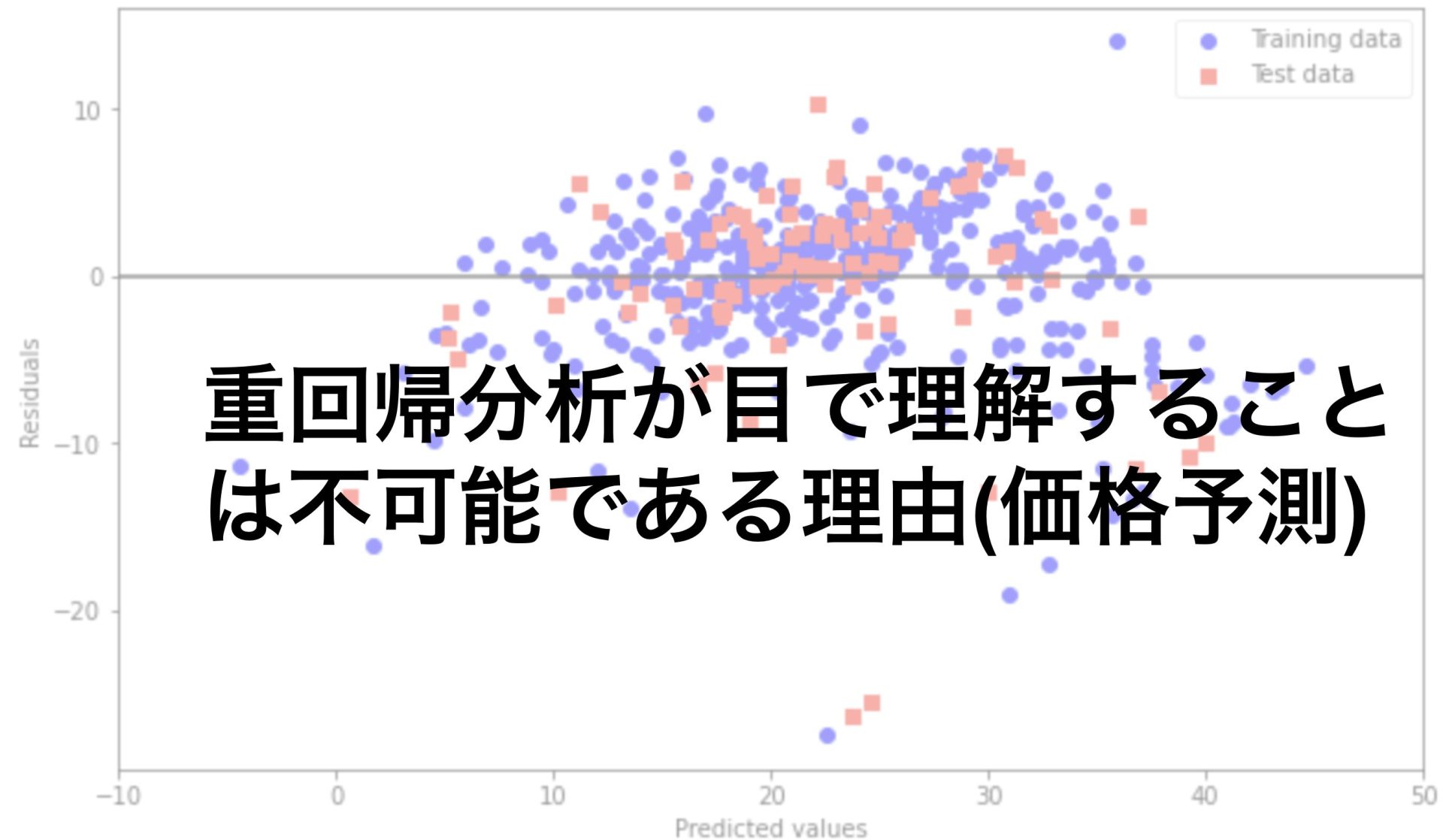
最後に予測値と実際の値の差をプロットしてみます。

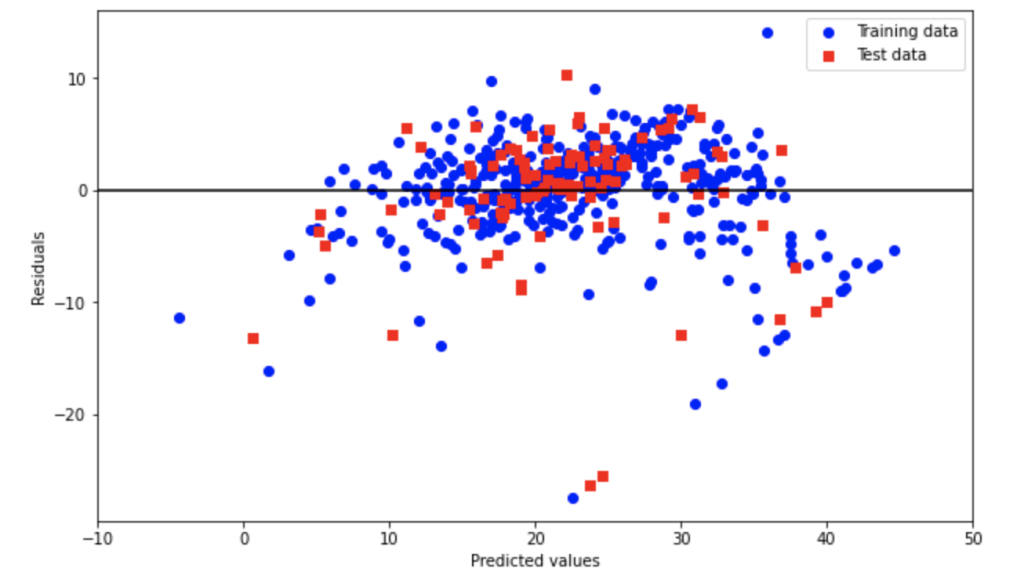
誤差が０付近に多くのデータが集まっていることがわかります。

今回の内容は以上です。

いかがだったでしょうか？

少ないコードで簡単に重回帰分析を行うことができるscikit-learnに感謝ですね。

最後に

という方向けにおすすめの講座を紹介したいと思います。

【おわりに】データサイエンスお勧め勉強法

結論から言うとUdemyというオンライン学習サービスのこちらの講座がおすすめです。

こちらの動画ではデータサイエンティストになるためのロードマップからそれぞれの分野について映像を用いた分かりやすい説明がなされています。

データサイエンスには以下の三つのスキルが必要と言われています。

この講座を受けると

・大学数学をあまり理解できていない

・プログラミングにあまり触れたことがない

・ビジネス経験がない

という方でも総合的な理解を深めて未経験からデータサイエンティストになることも可能だと思います。

スキルを身につけて安定を得たい、プログラミングの副業をやってみたいという方に特におすすめの講座です。

対象のUdemy講座はこちら

一緒に頑張っていきましょう。

ねこすけ

他にもいろんな記事を投稿してるにゃ。

関連記事

【データサイエンス】時系列データをプロットして移動平均線を表示してみよう(Python)

今回はデータサイエンスの入り口として実際の株価データを用いて移動平均線をプロットしていこうと思います。データサイエンス、機械学習などに興味がある方は特に必見です。

prog-you.com

2022.03.22

【初案件取得】実績０からPythonスクレイピング案件を獲得するまでの最短３ステップ

私が実績０から初案件を獲得するまでの方法を公開します。Pythonで稼ぎたい、スキルで安定を得たい、副業をしたいと思っている方は必見です。

prog-you.com

2021.12.13

【scikit-learn入門】ロジスティック回帰を使ってワイン分類をやってみよう

こんにちは。学生エンジニアのゆうき( @engieerblog_Yu )です。 今回はscikit-learnというデータ分析のライブラリを使ってワイン分類を行っていこうと思います。 データサイエンスを楽しんでいただけたら嬉しいです。

prog-you.com

2022.04.20