はじめに
こんにちは。将棋と筋トレが好きな、学生エンジニアのゆうき(@engieerblog_Yu)です。
今回はscikit-learnなどのライブラリの中で、何が起こっているのかを理解するために、連立方程式とLpノルムの関係について数学的に解説していきたいと思います。
連立方程式と解の数について
回帰分析とは、あるデータの集合から、データに最も当てはまりがよさそうな関数を探すことです。
その関数を探すためには、方程式の解を考えることが必要です。
関数を探すための解を見つける手段として、まずは連立方程式を考えます。
連立方程式は一般に以下のように表すことができます。
\(Ax = b \)
(A:行列 x:ベクトル b:ベクトル)
具体例で表すと
\(3x_1+2x_2+x_3=1\)
\(x_1+2x_2-x_3=3\)
\(2x_1-x_2+4x_3=5\)
という連立方程式を、行列とベクトルを使って表したものが以下です。
\(\left(\begin{array}{rr}3&2&1 \\1 & 2 & -1 \\2 & -1 & 4 \\\end{array}\right)\left(\begin{array}{rr} x_1 \\x_2 \\x_3\\\end{array}\right)=\left(\begin{array}{rr} 1 \\3 \\5\\\end{array}\right)\)
\(A=\left(\begin{array}{rr}3&2&1 \\1 & 2 & -1 \\2 & -1 & 4 \\\end{array}\right) x=\left(\begin{array}{rr} x_1 \\x_2 \\x_3\\\end{array}\right)\)
\(b=\left(\begin{array}{rr} 1 \\3 \\5\\\end{array}\right)\)
この時3つの式に対して3つの変数があり、解の組が一つに定まる問題を中学校あたりで解いていた人が多いんじゃないでしょうか。
例えば(x1,x2,x3)=(1,2,3)など。
しかし、一般に方程式の数と変数の数が変わってくると、解の組を決めることができません。
方程式よりも未知数の変数の数が多いものを劣決定系、方程式よりも未知数の変数の数が多いものを過決定系と言います。
例えば
以下は劣決定系の例です。
\(\left(\begin{array}{rr}3&2&1 \\1 & 2 & -1 \\\end{array}\right)\left(\begin{array}{rr} x_1 \\x_2 \\x_3\\\end{array}\right)=\left(\begin{array}{rr} 1 \\3 \\\end{array}\right)\)
以下が過決定系です。
\(\left(\begin{array}{rr}3&2&1 \\1 & 2 & -1 \\2 & -1 & 4 \\3&2&6\end{array}\right)\left(\begin{array}{rr} x_1 \\x_2 \\x_3\\\end{array}\right)=\left(\begin{array}{rr} 1 \\3 \\5\\4\end{array}\right)\)
劣決定系では解が無限に存在し、過決定系では解を決めることができません。
回帰分析ではそのような解が定まらないような問題を考えます。
そのためにノルムを使った、制約やペナルティを考える必要があります。
回帰について
それでは本題の回帰についてのお話です。
今回は(x1,y1),(x2,y2)・・・(xn,yn)
これらのn個の点を通る最適な直線を求めます。
これは、先ほどの連立方程式の解に相当します。
これらの解を通る直線を考えます。
\(f(x)=β_1x+β_2\)
β:定数
以下の図の青い点が、xとyの解の集合だった場合、直線はどうなるでしょうか。
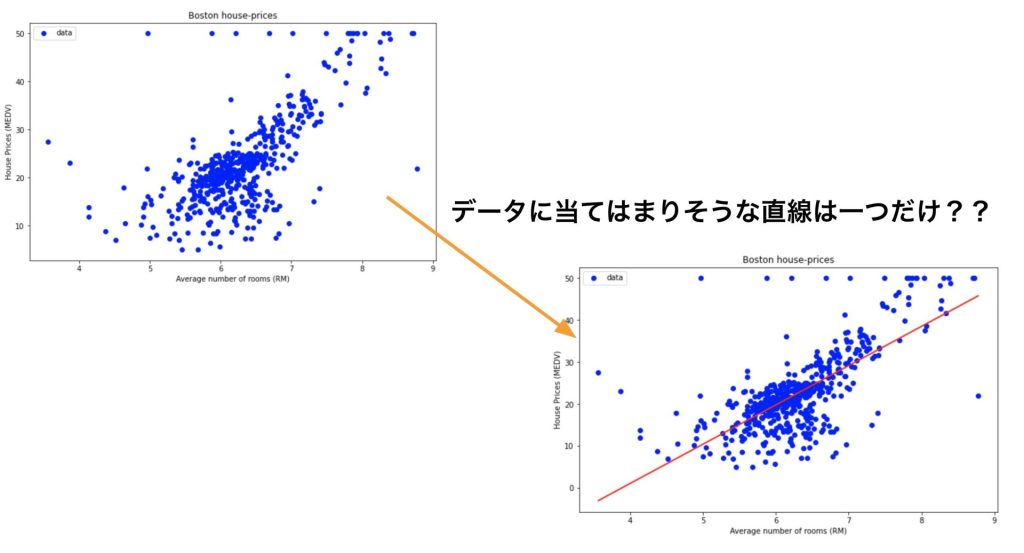
データに当てはまりそうな直線が何本もありそうですね。
これはいわゆる先ほどの、解の組が定まらないといった例になります。(今回はxとyなので2次元)
データに当てはまりそうな直線を引くために、ノルムを考える必要があります。
ノルムを考えることで、条件を緩和して(制約をつける)、直線を引くことができます。
標準的に使われる誤差指標として、L2,L1,L∞ノルムというものがあるので、そちらについて解説していきたいと思います。
Lpノルムについて
データに当てはまりそうな直線を引くために、誤差EのLpノルムというものを考えます。
各点での誤差\(E_k\)は次の式で与えられます。
\(f(x_k)=y_k+E_k\)
pは変数であり、0~∞の値を取ります。
以下がLpノルムの定義式です。
\(E_p(f)=(\frac{1}{n}\sum_{k=1}^{n}|f(x_k)-y_k|^{p})^{1/p}\)
例えば、L2ノルムを考えてみます。
\(E_2(f)=(\frac{1}{n}\sum_{k=1}^{n}|f(x_k)-y_k|^{2})^{1/2}\)
これは各点での二乗誤差を足して、平均を取ってから、ルートを取ったものです。
L2ノルムを使った誤差評価(最小二乗法)に関しましては、こちらの記事でも解説しています。
同様にL1ノルムとL∞ノルムはこのように定義されます。
\(E_1(f)=\frac{1}{n}\sum_{k=1}^{n}|f(x_k)-y_k|\)
\(E_∞(f)=\max_{1<k<n}|f(x_k)-y_k|\)
Lpノルムを使った誤差Eは以下で定義され、L1,L2,L∞ノルムが一般によく使われる
\(E_p(f)=(\frac{1}{n}\sum_{k=1}^{n}|f(x_k)-y_k|^{p})^{1/p}\)
このようにLpノルムで定義される誤差指標の値が、最も小さくなるように直線を引きます。
また誤差指標としてL∞ノルムを用いた場合、外れ値に影響されやすくなります。
反対にL1ノルムを用いた場合は、外れ値の影響が小さくなります。
以下の図を見ると、xが2の時に外れ値があるのが分かります。
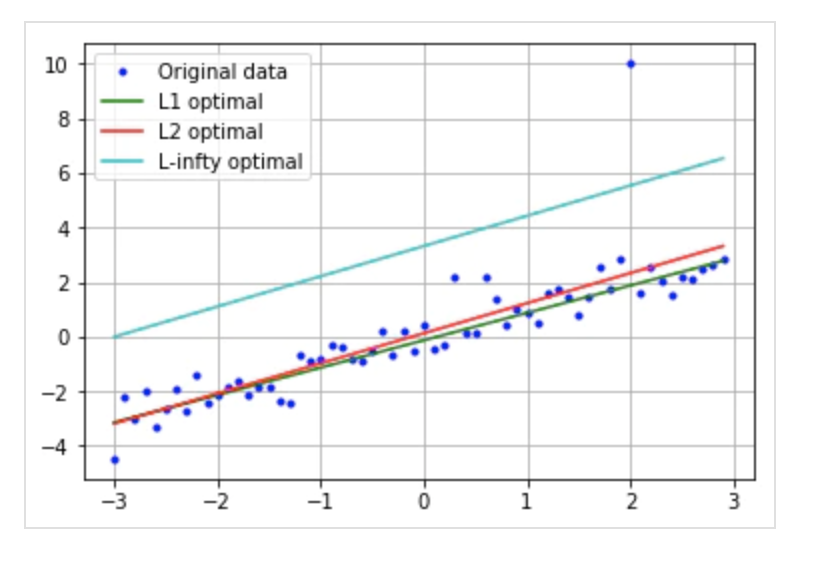
Lpノルムのpが大きくなればなるほど、直線が外れ値に影響されやすくなることがわかると思います。
誤差指標にLpノルムを使った場合、pが大きくなればなるほど外れ値に影響されやすくなる
外れ値に影響されやすくなるという表現は悪いように思えますが、実際そうではありません。
回帰分析を行う際に、過学習を行なってしまい、未知のデータへの当てはまりが悪くなってしまった場合、ノルムを大きくすることで制約(ペナルティ)を小さくできます。
まとめ
回帰分析とは、解が定まらない連立方程式を解くための手段
Lpノルムを使って制約をつけることで連立方程式を近似的に解くことができる
Lpノルムのpを大きくすればするほど外れ値に影響されやすくなり、過学習の抑制に効果的

他にもいろんな投稿があるにゃ。




コメント