はじめに
どーも、情報系大学生のゆうき(@engieerblog_Yu)です。
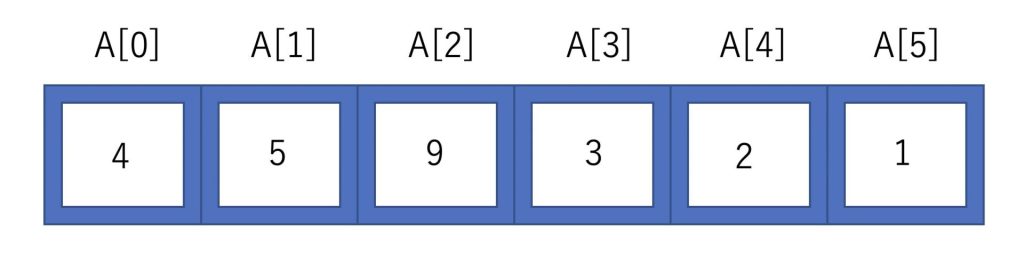
今回はこのような配列を昇順(小さい順)に並び替えていくことを考えましょう。
みなさんはどのように整列しようと考えるでしょうか?
整列の方法はいろいろありますが、計算量の観点でどのような整列アルゴリズムを選ぶかが大切になってきます。
今回はその中でバブルソート、挿入ソート、シェルソートをまとめていきたいと思います。
計算量のオーダー記法について怪しい方はこちらの記事も併せてどうぞ。
他にも整列アルゴリズムについての記事を投稿しています。
バブルソート
バブルソートは値が交換されて、泡のように上昇していくことに由来しています。
バブルソートでは、①から⑤の順に隣り合う値を比較して、一つ後の数の方が小さかったら入れ替えていきます。
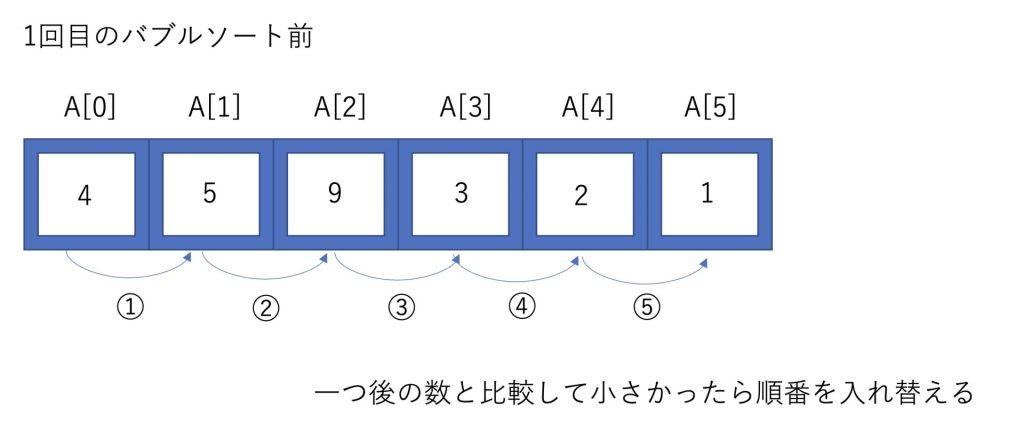
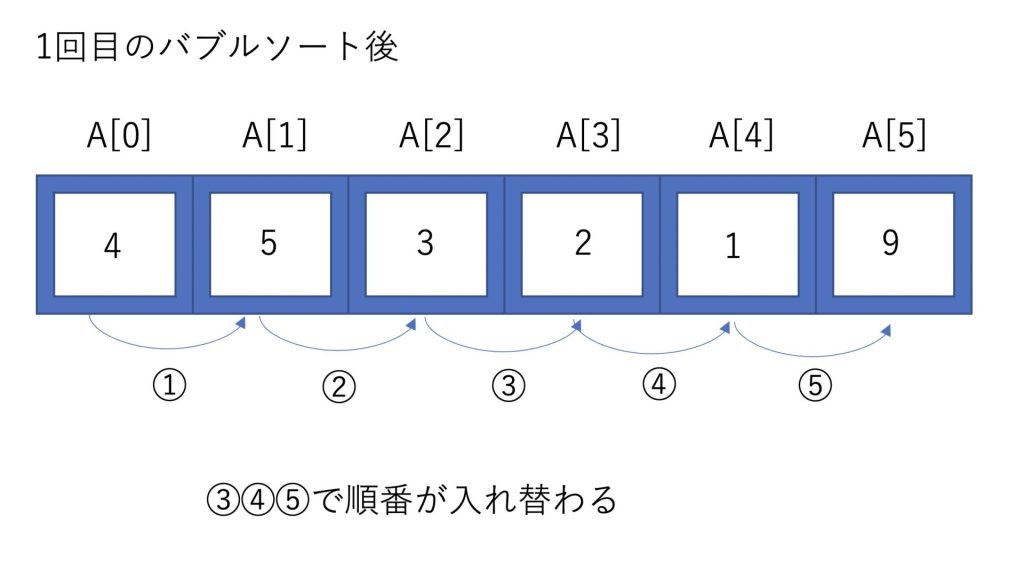
今回は3、4、5で順番が入れ替わります。
2回目のバブルソートでは最後の要素に一番大きい値が入っていることが確定しているため、⑤の比較は要りません。
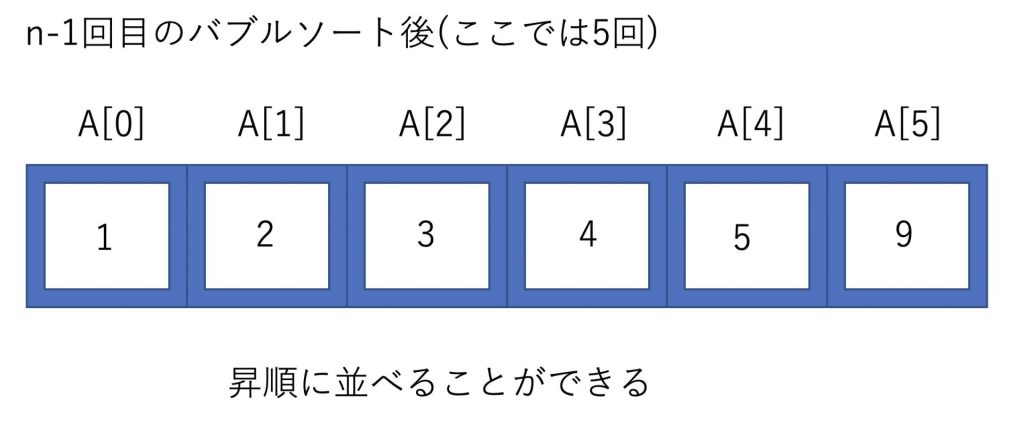
バブルソートはn-1回繰り返します。(要素数n)
n-1回繰り返すと、昇順にソートできていることが分かります。
比較回数はn(n-1)/2となります。
バブルソートの計算量はO(n^2)となります。
ただしデータの交換が一切起こらなかった場合にすでに整列済みと見做し、処理を終了させることでO (n)に抑えられる場合もあります。
挿入ソート
挿入ソートでは整列済みの部分を左に作っていき、値を適切な位置に順番に格納していく方法です。
まずはA[0]を整列済みと見做してA[1]をどこに挿入するのが適切か調べます。

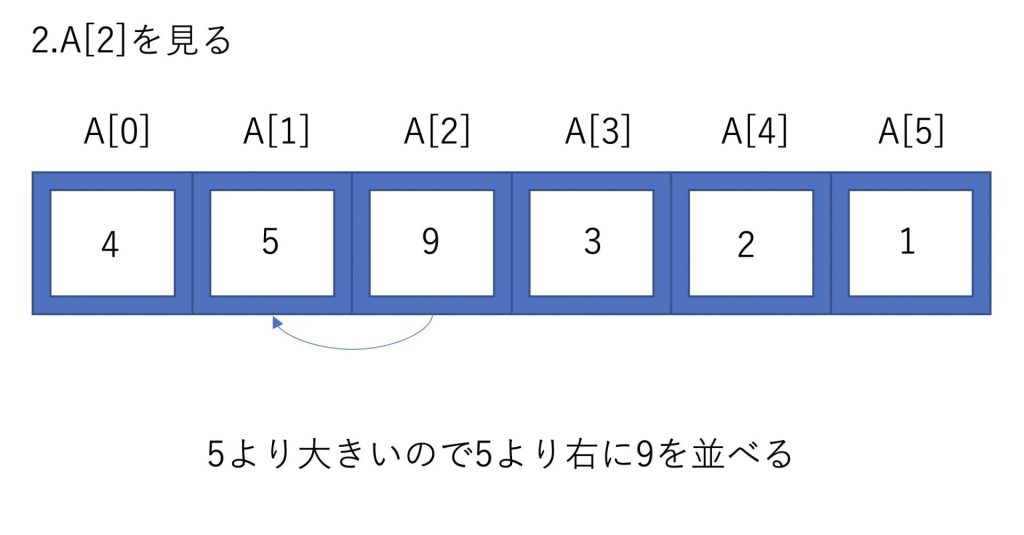
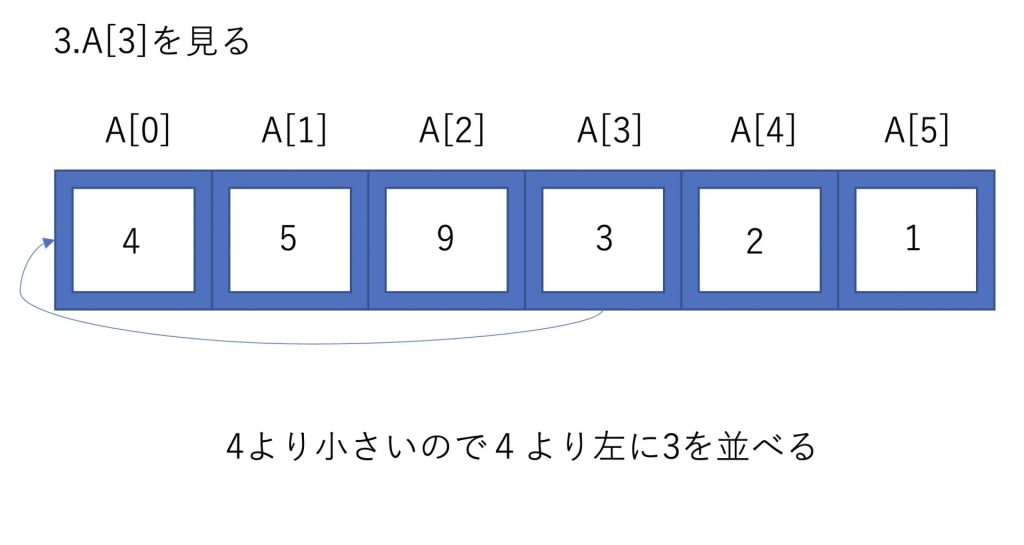
この時点で整列済みは3、4、5、9となります。
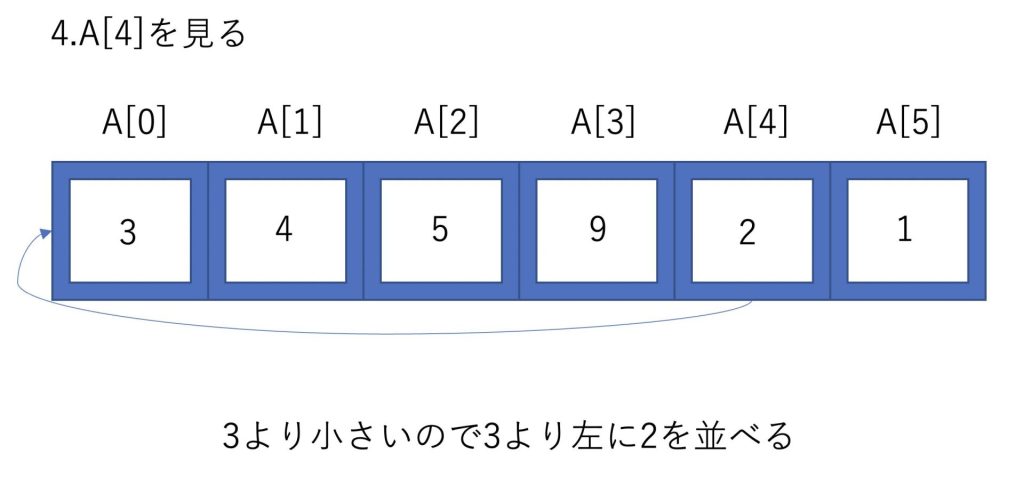
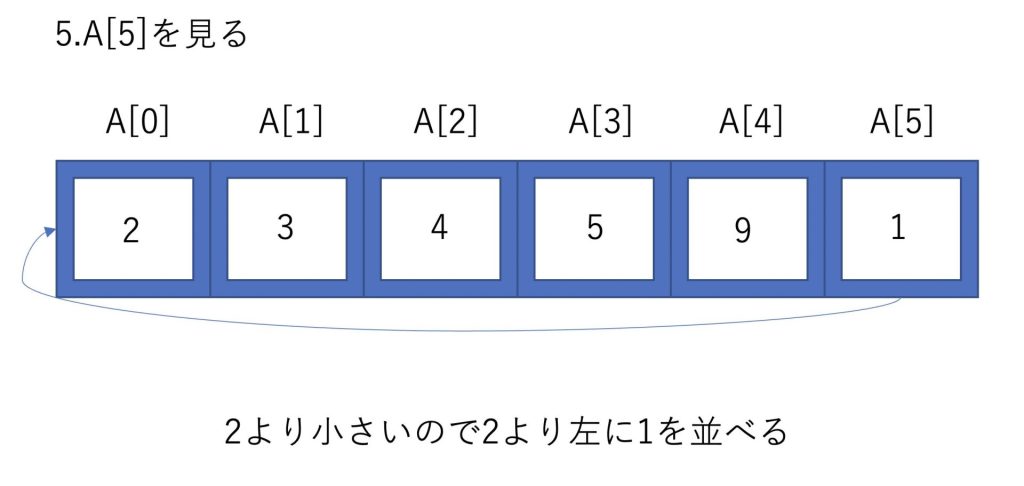
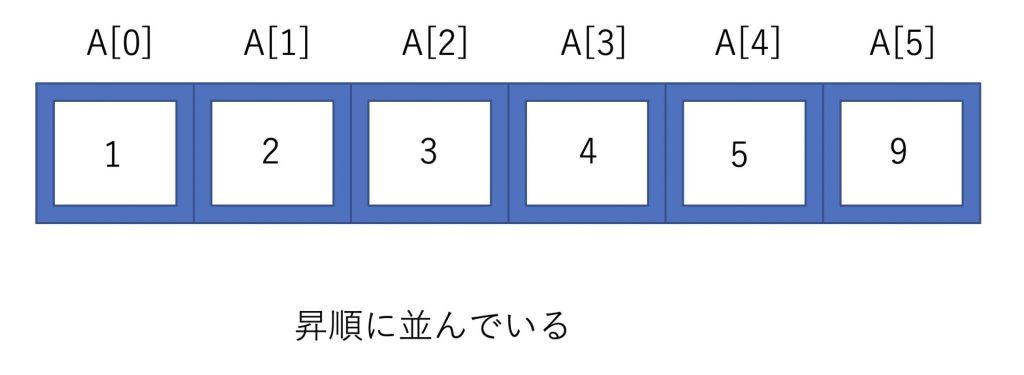
このようにして昇順に並べることができました。
挿入ソートの計算量は最良でO(n)となり、最悪でO(n^2)となります。
シェルソート
シェルソートとはギャップというものを設定し、ギャップ毎に並べた配列を挿入ソートで並べます。
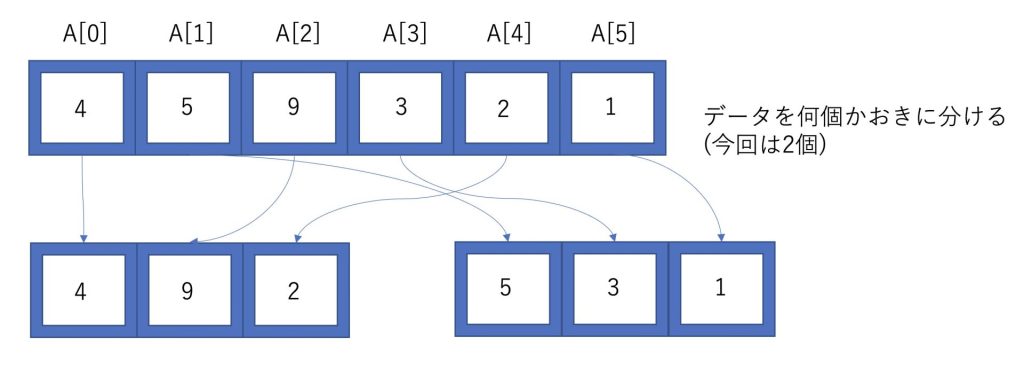
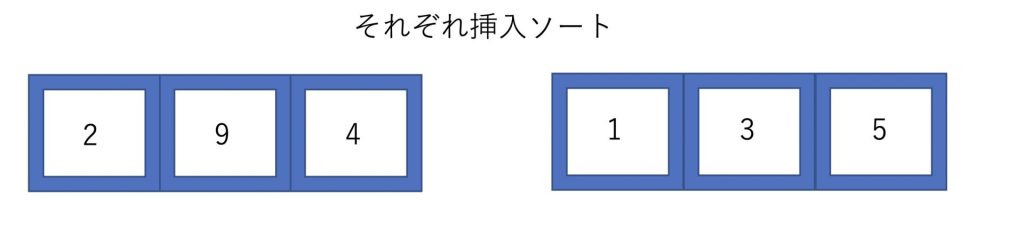
その後それぞれの配列を挿入ソートします。
挿入ソートで並べた配列を元のギャップごとの位置に戻します。
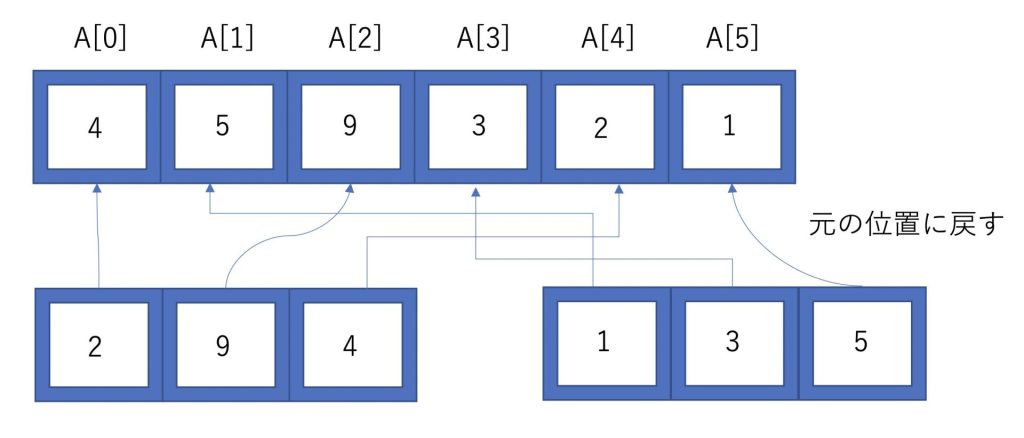
その後に普通の挿入ソートを行います。

シェルソートの計算量はギャップ列に依存し、ギャップ列によって異なりますが、挿入ソートよりも計算量が小さくなることが多いです。
まとめ
バブルソートの計算量は最良O(n)、最悪O(n^2)
挿入ソートの計算量は最良O(n)、最悪O(n^2)
シェルソートの計算量はギャップ列に依存し、挿入ソートよりも小さくなることが多い
アルゴリズムの勉強におすすめの書籍です。

読んでいただきありがとうございました。

他にもいろんな記事があるにゃ。





コメント