初めに
こんにちは、情報系大学生のゆうき(@engieerblog_Yu)です。
今回から、基本・応用情報技術者試験や、情報系が大学で学ぶ内容についてまとめていきたいと思います。
今回は、2・8・10・16進数の基数変換について解説します。
2進数とは?

2進数とは、0と1の二つの数字のみを使って数を表そうとしたものです。
私たちが普段使っている10進数は0~9の数字を使って、数を表したものです。
なぜ2進数を考える必要があるのかというと、コンピュータは電気のON、OFFで動いているからです。
ON→1、OFF→0にあたります。(この最小単位をビット(bit)と呼びます。)
よってコンピュータの中身を理解するためには、2進数を理解することが必要です。
2進数で数を表すと以下のようになります。()は10進数です。
0(0)→1(1)→10(2)→11(3)→100(4)→101(5)→110(6)→111(7)→
本来なら2と書くべきところで繰り上がりを行う訳ですね。
2進数で表すことのできる数の範囲は、1桁あたり1ビットとなります。
つまり1桁→1ビット、2桁→2ビット、3桁→3ビットで表現することができます。
1ビットあたり0,1の2パターンがあるので、\(2^{桁数}\)通りの数が表せるわけです。
2進数とは、0と1の二つの数字のみを使って数を表そうとしたもの
2進数で表すことのできる数の範囲は、\(2^{桁数}\)通り
8進数と16進数について
8進数と16進数も2進数と考え方は同じです。
8進数は8個の数字で、16進数は16個の数字で表したものです。
\(8=2^{3} 16=2^{4}\)となることに気をつけると、以下が成り立ちます。
8進数の1桁が持つ情報量=2進数の3桁が持つ情報量
16進数の1桁が持つ情報量=2進数の4桁が持つ情報量
つまり、8進数が表すことができる数の範囲は、\(2^{3×桁数}\)、16進数が表すことができる数の範囲は、\(2^{4×桁数}\)となります。
8進数の1桁が持つ情報量=2進数の3桁が持つ情報量
16進数の1桁が持つ情報量=2進数の4桁が持つ情報量
8進数が表すことができる数の範囲→\(2^{3×桁数}\)
16進数が表すことができる数の範囲→\(2^{4×桁数}\)
バイトを表す数に16進数が使われる
バイトは8ビットを1単位とします。
つまり1バイトは、\(2^{8}\)通りの数を表すことができます。
ここで16進数で表せる数は、\(2^{4×桁数}\)ですので、1バイトは、二桁の16進数で表すことができます。
よって互換性があるので、バイトは16進数で表されることが多いです。
バイトは8ビットを1単位したもの
1バイトは、\(2^{8}\)通りの数を表すことができる
1バイトは、二桁の16進数で表せる
n進数→10進数の基数変換
n進数を10進数に直すためには、各桁の数に重みをかけて足し合わせます。
例えば、7進数の164を10進数に直したい場合、以下の計算を行います。
\(4×7^{0}+6×7^{1}+1×7^{2}\)
補足:小数点以下がある場合
7進数0.153は\(1×7^{-1}+5×7^{-2}+3×7^{-3}\)で10進数に変換できます。
10進数→n進数の基数変換
10進数をn進数に基数変換するためには、10進数の数をnで割っていった余りを下から見たものが答えとなります。
わかりにくいと思うので、例を挙げます。
13という10進数を2進数に変換していきます。
やり方は以下になります。
①13を2で割っていき、余りを右に書き出していく
②0になるまで①を繰り返す
③余りを下から上に見たものが2進数に基数変換したもの
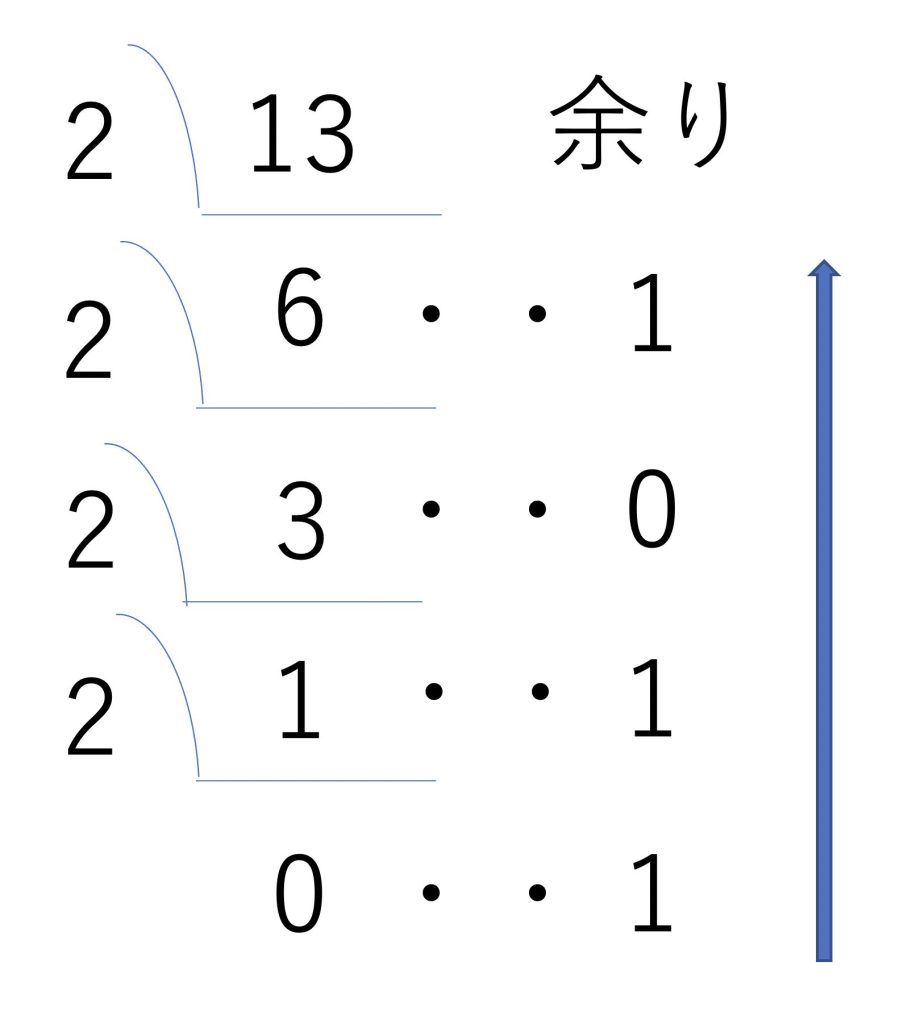
今回の場合は1101(2進数)が答えとなります。
まとめ

2進数とは、0と1の二つの数字のみを使って数を表そうとしたもの
2進数で表すことのできる数の範囲は、\(2^{桁数}\)通り
8進数が表すことができる数の範囲→\(2^{3×桁数}\)
16進数が表すことができる数の範囲→\(2^{4×桁数}\)
1バイトは、二桁の16進数で表せる
今回は、2・8・10・16進数の基数変換について解説しました。
今回の内容は、情報技術者試験に含まれている内容になります。
関連記事
情報系の大学生の方、情報系に興味がある方、情報系に就職を考えている方は情報技術者試験をとることをおすすめします。
ざっくり以下のようなイメージです。
基本情報技術者→情報系の学部1・2年で学ぶ内容
応用情報技術者→情報系の学部3・4年で学ぶ内容
特に応用情報技術者試験に合格すると、情報系の就職にかなり有利になったり、会社で優遇されたりします。
私が情報技術者試験の学習に使った、おすすめ書籍は以下になります。
めちゃくちゃわかりやすいので、情報系でない方でも、すらすら読み進めることができると思います。
おすすめ書籍

最後まで読んでいただきありがとうございました。





コメント